Ім'я файлу: 94507.docx
Розширення: docx
Розмір: 799кб.
Дата: 24.11.2020
скачати
Пов'язані файли:
Сферична геометрія.docx
Розширення: docx
Розмір: 799кб.
Дата: 24.11.2020
скачати
Пов'язані файли:
Сферична геометрія.docx
3.1.4.Заняття № 4.
Тема уроку: Задачі, що зводяться до розв’язування рівнянь із одним невідомим у цілих числах, використовуючи властивості подільності чисел.
Мета уроку:
- продовження формування вміння розв’язувати текстові задачі
- сформувати вміння розв’язувати задачі, що зводяться до розв’язування рівнянь у цілих числах.
Хід уроку:
На початковому етапі уроку слід перевірити домашнє завдання.
Сформувати алгоритми розв’язування діофантових рівнянь, використовуючи властивості подільності чисел.
Задача 1: Фірма заказала 143 комп’ютери, для того щоб розподілити їх між своїми філіями порівну. Однак потім фірма вирішила відкрити ще дві філії, і в результаті кожна філія отримала на 2 комп’ютери менше.
Скільки у фірми стало філій?
Розв’язання:
Позначимо початкову кількість філій через
. Тоді за умовою задачі кожна філія повинна була отримати 
комп’ютера. Але філій стало 
, і, отже кожна філія отримала 
комп’ютери.За умовою задачі кожна філія отримала на 2 комп’ютери менше.
Складемо рівняння:
.Згадаємо, що
- кількість філій фірми і, отже – це натуральне число. Крім того та - теж натуральні числа, оскільки кожне із них – це кількість комп’ютерів.Отже, числа
та - дільники числа 143. Залишається знайти усі дільники числа 143 та вибрати такі два дільники, один із яких на 2 більше другого.У числа 143 лише чотири дільники:
.Перебравши усі можливі пари дільників, легко побачити, що умові задовольняє лише пара чисел 11; 13.
Отже
, а 
.Відповідь: у фірмі стало 13 філій.
Задача 2: Андрійко задумав деяке натуральне число. Борис запропонував йому піднести це число до другого степеня, після цього додати задумане число і назвати результат. Результат дорівнював 90. Як Борису дізнатись, яке число задумав Андрій?
Розв’язання:
Позначимо задумане число через
. Тоді можна скласти рівняння:
або 
.Тепер ясно, що треба знайти натуральне число
таке, що при множенні його на наступне натуральне число у добутку будемо мати 90. Такі два натуральні числа неважко підібрати – це 9 та 10.Отже,
.Здається, що задача розв’язана, але це не так. Раптом є ще будь-яке натуральне число, що задовольняє умові
? Бо в даному випадку ми не перебирали усі можливі варіанти розв’язків, а лише підібрали відповідь.Для того, щоб впевнитись у відсутності іншого такого числа, треба провести додаткові міркування: якщо
то 
, тоді добуток 
більше 
, тобто більше 90. Аналогічно:
не може бути менше 9, бо в цьому випадку добуток 
. Отже могло бути задумане лише число 9.Відповідь: задумане число 9.
Дуже часто в олімпіадних задачах зустрічаються такі, що зводяться до розв’язування системи нелінійних рівнянь, що мають кількість невідомих більшу ніж кількість рівнянь, у цілих числах. Тому у курс обов’язково треба включити такі завдання для загального ознайомлення. Деякі системи зводяться до розв’язування діофантового рівняння, використовуючи властивості подільності чисел. Пропонуємо включити декілька систем у цей урок.
Приклад 1: Розв’язати в натуральних числах:
Розв’язання:
Віднімемо почленно із першого рівняння системи друге:
В результаті отримаємо:
Тепер треба перетворити ліву частину таким чином, щоб отримати добуток многочленів:
Тепер за звичною системою: розглянемо усі розкладення числа 48 на дільники.
Маємо ряд систем:
1)
2) 
3) 
4) 
5)
6) 
7) 
8) 
9)
10) 
Розв’язавши ці системи, знаходимо два розв’язки у натуральних числах рівняння:
.
; 
.Тепер треба повернутися до вихідної системи, з метою її розв’язків. Для цього у будь-яке рівняння системи підставляємо отримані пари чисел і знаходимо розв’язки самої системи, а саме:
Підставимо наші пари чисел у перше рівняння системи:
Якщо
, 
, то 
. Тобто, розв’язком системи в цьому випадку є трійка чисел: 
.Якщо
, 
, то 
. Тобто, розв’язком системи в цьому випадку є трійка чисел: 
.Для самостійної роботи учнів:
Приклад 2: Знайти усі натуральні
, 
, 
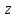, що задовольняють системі:
Розв’язок:
Віднімемо перше рівняння від другого:
Перетворимо ліву частину у добуток многочленів:
З цього рівняння отримуємо дві системи:
1)
2) 
Для першої системи:
Підставляємо ці значення ц вихідну систему і отримаємо, в цьому випадку, розв’язок у вигляді:
.Приклад: Знайти натуральний розв’язок рівняння:
.Розв’язок:
Дільники числа 6:
.Нас задовольняють два числа, які відрізняються на одиницю і у добутку дають число 6. Легко бачити, що це числа 3 і 2.
Отже,
.Приклад 3: знайти натуральні розв’язки рівняння:
Відповідь:
.Домашнє завдання:
1) Знайти натуральний корінь рівняння:
Відповідь:
2) Знайти усі цілі корені рівняння:
Відповідь:
; 
.3) Знайти натуральні корені рівняння:
Відповідь:
.3.1.5.Заняття № 5.
Тема уроку: Розв’язування діофантових рівнянь методом виділення цілої частини.
Мета уроку:
- сформувати вміння розв’язувати діофантові рівняння методом виділення цілої частини.
- продовження формування вміння розв’язувати текстові задачі.
Хід уроку:
Метод виділення цілої частини – є загальним методом для розв’язання у цілих числах невизначених (діофантових) рівнянь. Він був названий у Індії методом розсіювання (роздроблення). Натяки саме на таке розв’язування зустрічаються вперше у працях індійського астронома Аріабхатти, подібне розв’язування виклали індійські математики Брахмагупта та Бхагкара, бо саме у Індії невизначені рівняння розв’язувалися із астрономічними запросами та календарними розрахунками, тому ними займались астрономи та математики.
Використаємо цей метод для розв’язування наступних задач.
Задача 1: Знайти два цілих числа, якщо відомо, що різниця добутків першого на 19 і другого на 8 дорівнює 13.
Розв’язок:
У задачі треба знайти усі цілі розв’язки рівняння:
(1).Виразимо
- невідоме з найменшим за абсолютною величиною коефіцієнтом- через , отримаємо: 
(2).Тепер треба дізнатись, при яких цілих значеннях
відповідні значення є також цілими числами. Перепишемо рівняння (2) у наступному вигляді: 
(3).З таким прийомом ми вже зустрічалися при розгляді попереднього метода. Із (3) випливає, що
при цілому приймає цілі значення тільки в тому випадку, якщо вираз 
є цілим числом, наприклад 
.Поклавши
(4), питання зводимо до розв’язку у цілих числах рівняння (4) з двома невідомими і ; його можна записати так:
(5).Це рівняння у порівнянні із вихідним має перевагу: 3 – найменша із абсолютних величин коефіцієнтів при невідомих – менша, ніж у (1), тобто 8. Це було досягнуто завдяки тому, що коефіцієнт при
(19) було замінено залишком від ділення на 8. Продовжуючи аналогічним способом, ми із (5) отримаємо:
(6)Отже, невідоме
при цілому тільки тоді приймає цілі значення, коли 
є ціле число, скажемо 
:
(7)або
(8)Далі,
(9)Покладемо
(10)отримаємо рівняння:
(11)Це саме просте із всіх розглянутих невизначених рівнянь, бо один із коефіцієнтів дорівнює одиниці.
Із (11) отримаємо:
(12)Звідси видно, що
приймає цілі значення при будь яких цілих значеннях 
. Із рівностей (6), (9), (12), (3) шляхом послідовних підстановок можна знайти наступні вирази для невідомих і рівняння (1):
Таким чином формули:
, при 
дають цілі розв’язки рівняння (1).Наведемо приклади розв’язків у таблиці.
| | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| | 7 | 15 | 23 | 31 | 39 | 47 | 55 | 63 | 71 |
| | 15 | 34 | 53 | 72 | 91 | 110 | 129 | 148 | 167 |
Цей прийом майже повністю співпадає із методом індійців і був названий ними методом розсіювання саме тому, що невизначене рівняння зводиться до ланцюга рівнянь із все меншими, за абсолютною величиною, коефіцієнтами.
Цей приклад треба розглядати дуже детально, записувати пояснення до кожного кроку, бо розв’язання є алгоритмом розв’язку діофантових рівнянь таким методом.
До розв’язування таких невизначених рівнянь зводяться іноді задачі, пов’язані із практикою і повсякденною діяльністю людини.
Задача 2: Чоловік купує у магазині річ вартістю у 19 крб. У нього є лише 15 купюр по три крб., у касира лише 20 купюр по п’ять крб. Чи можна розрахуватися і як?
Розв’язання:
Задача зводиться до розв’язку у цілих додатних числах числах діофантового рівняння:
, де 
, 
Більш того
, бо 
Далі,
, 
, 
, 
.Звідки
, 
.В силу того, що
і повинні бути додатними, та враховуючи умову задачі, легко встановити, що 
,тобто
може приймати тільки два значення: 0; 1. Звідси випливають два можливі розв’язки. | | 8 | 13 |
| | 1 | 4 |
Для самостійного розв’язку учнів:
Задача 3: Чи можна зважити 28 г деякої речовини на терезах, маючи тільки чотири ваги масою 3 г і сім - масою 5г?
Розв’язання:
Розв’яжемо діофантове рівняння:
Маємо:
,
, 
,
Отже,
Із умови задачі випливає, що
не може набувати від’ємні значення (бо це призведе до від’ємного ).Також
, отже, 
.Однак
і 
суперечить умові задачі, тобто за умовою 
. Таким чином, можливо лише 
. При цьому 
, 
єдиний розв’язок задачі.Багато старовинних способів відгадування чисел і дат народження засновано на розв’язанні діофантових рівнянь.
Задача 4:
Ви пропонуєте товаришу помножити число дати його народження на 12, а номер місяця – на 31. Він повідомляє вам суму обох добутків, а ви розраховуєте по ній дату народження друга.
Якщо, наприклад, товариш ваш народився 9 лютого, то він робить наступне:
, 
, 
Це останнє число, 170, він вам повідомляє, а ви з’ясовуєте задуману дату. Як?
Розв’язання:
Задача зводиться до розв’язку невизначеного рівняння:
У цілих і додатних числах, причому число місяця
не більше 31, а номер місяця не більше 12.
,
, 
Знаючи, що
і 
знаходимо границі для 
: 
.Отже:
, , 
.Дата народження 9-е число другого місяця, тобто 9 лютого.
Для самостійного розв’язку учнів:
Задача 5: Знайти дату народження, якщо сума добутків дорівнює 330.
Розв’язання:
Розв’яжемо невизначене рівняння:
За допомогою метода розсіювання отримаємо:
Із умови
Легко констатувати, що єдине рішення
, 
, 
.Отже, дата народження: 12-е число, 6-го місяця, тобто 12 червня.
Домашнє завдання:
Задача 6: Треба на один карбованець купити 40 штук поштових марок: по одній копійці – по 4-и копійки і по 12 копійок. Скільки марок кожної ціни можна купити?
Розв’язання:
У даному випадку маємо два рівняння із трьома невідомими:
де:
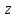- кількість марок по копійці; - по 4 копійки; - по 12 копійок.Віднімемо із першого рівняння друге, одержимомо одне рівняння з двома невідомими:
Знаходимо
:
,
, 
, 
.Підставимо вирази для
і 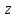у друге із вихідних рівнянь:
Одержуємо:
Так як
, 
, 
.
Тобто
, 
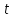 | 0 | 1 |
| | 20 | 28 |
| | 20 | 9 |
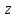| | 0 | 3 |
Перевірка:
Отже, марки можна купити двома способами.
Перед тим як задати цю задачу додому треба зробити коментар до неї, а саме пояснити як скласти систему рівнянь.
Другу аналогічну задачу задати без коментарю.
Задача 7:
На 5 крб. купити 100 різних фруктів. Ціни на фрукти такі:
| кавун | шт. | 50 коп. |
| яблуко | шт. | 10 коп. |
| слива | шт. | 1 коп. |
Скільки фруктів кожного роду було куплено?
Відповідь: 1 кавун, 39 яблук, 60 слив.
1 2 3 4 5