Ім'я файлу: 94507.docx
Розширення: docx
Розмір: 799кб.
Дата: 24.11.2020
скачати
Пов'язані файли:
Сферична геометрія.docx
Розширення: docx
Розмір: 799кб.
Дата: 24.11.2020
скачати
Пов'язані файли:
Сферична геометрія.docx
1.2.2. Рівняння другого степеня з двома невідомими.
Теорема II(без доведення). Будь – який розв’язок рівняння
(12) при додатному 
та ірраціональному
має вигляд
, де 
(13)а
- найменший розв’язок.Наприклад, найменшим розв’язком рівняння
буде 
, 
, усі розв’язки цього рівняння будуть міститись у формулах:
,
,Звідки при
, ми отримуємо розв’язки: 
.Відмітимо, що числа
та 
із зростанням n зростають із швидкістю геометричної прогресії із знаменником 
,так як внаслідок рівності ( )(
)=1 ми можемо стверджувати, що 0<
<
<1 і тому (
)
завжди прямує до 0 із зростанням n.ТЕОРЕМА III(без доведення). При будь-якому цілому додатному А та ірраціональному
рівняння (12) має розв`язок , 
, 
.У випадку другого степеня пари цілих чисел, які можуть бути розв’язками рівняння, зустрічаються значно рідше, ніж пари цілих чисел, що можуть бути розв’язками рівняння першого степеня.
1.3. Рівняння з двома невідомими степеня вище другого.
a0xn + a1xn-1y + a2xn-2y2 + … + anyn , (14)
де n – ціле число, більше за 2, і всі числа a0, a1, a2, …, an, c – цілі числа.
Рівняння з двома невідомими степеня вище другого майже завжди можуть мати тільки кінцеву кількість розв’язків у цілих числах х та у.
.Алгебраїчні рівняння вищих порядків із трьома невідомими.
Якщо для рівнянь з двома невідомими ми можемо дати відповідь на питання про існування кінцевої або нескінченої кількості розв’язків у цілих числах, то для рівнянь вищих порядків з кількістю невідомих більше ніж два дати відповідь на це питання ми можемо лише для деяких окремих класів рівнянь. Видатний французький математик П’єр Ферма висловив твердження, що рівняння
xn + yn = zn (15)
при цілому n
2 не має розв’язків у цілих додатніх числах x, y та z (випадок xyz = 0 виключається додатністю x, y, z.Таким чином, загальна теорія розв’язування рівнянь у цілих числах повністю розроблена тільки для рівнянь першого та другого степенів із двома невідомими. Для рівнянь вищих степенів з двома та більш невідомими дуже складна не тільки задача знаходження усіх розв’язків у цілих числах, але і більш проста задача встановлення існування кінцевої або нескінченної множини таких розв’язків.
На факультативних заняттях доцільно познайомити учнів з найпростішими випадками діофантових рівнянь та методами їх розв’язування, із загальними методами розв’язування лінійних діофантових рівнянь.
2. Методика підготовки учнів до розв’язання олімпіадних задач, пов’язаних із діофантовими рівняннями.
2.1. Принципи відбору теоретичного матеріалу:
Принцип науковості та посильної складності, який передбачає відповідність запропонованого матеріалу рівню сучасної науки, збереження наукової системи у певній послідовності, а також міжпредметних зв’язків разом із врахуванням у процесі навчання вікових та індивідуальних особливостей учнів.
Принцип розвитку теоретичного мислення. Передбачає розвиток теоретичного та логічного мислення учнів.
Принцип систематичності. Реалізується за допомогою цільової і логічної систематизації, які повинні допомогти учням оволодіти системними знаннями.
Принцип переходу від навчання до самонавчання і розвиток пізнавальних сил учнів. Сутність цього принципу полягає у пристосуванні навчання до змісту та рівня знань та вмінь, навичок кожного учня з метою виховання творчого підходу при вивченні кожного питання, вміння критично оцінювати результати своєї роботи, здатність до самоконтролю та самонавчання.
Практична важливість і зв’язок матеріалу із досвідом учнів. Передбачає можливість подання матеріалу на основі вивченого учнями раніше та можливість запропонувати учням нові нестандартні методи розв’язання математичних задач з метою активізувати процес навчання.
Перспективне значення матеріалу. Передбачає можливість використовувати його у подальшій учбовій діяльності.
2.2. Найпростіші методи розв’язування діофантових рівнянь.
Метод повного перебору.
Використання властивостей подільності.
Виділення цілої частини.
3. Додатки.
3.1. Розробка факультативних занять за темою «Діофантові рівняння».
3.1.1. Заняття № 1.
Тема уроку: Діофант та діофантові рівняння. Розв’язування діофантових рівнянь методом повного перебору.
Тип уроку : Засвоєння нових знань, вмінь
Мета уроку: - ознайомити учнів із поняттям діофантового рівняння;
- сформувати вміння розв’язувати діофантові рівняння,
використовуючи метод повного перебору.
Хід уроку:
Перший етап даного уроку треба присвятити ознайомленню учнів із питаннями історії діофантових рівнянь. Для цього доцільно запропонувати учням самостійно підготувати реферат за темою «Про Діофанта та діофантові рівняння».
Означення: Діофантові рівняння – алгебраїчні рівняння або системи рівнянь із раціональними коефіцієнтами, розв’язки яких знаходять у цілих або раціональних числах. Зазвичай припускають, що діофантові рівняння мають кількість невідомих більшу, ніж кількість рівнянь, у зв’язку з цим вони також називаються невизначеними рівняннями.
Найпростішими методами розв’язування діофантових рівнянь є:
- метод повного перебору;
- метод, пов’язаний із використанням властивостей подільності чисел;
- метод, пов’язаний із виділенням цілої частини або метод розсіювання.
Найбільш простим методом розв’язання діофантових рівнянь є метод повного перебору, тому заняття слід почати із розгляду декількох рівнянь, що розв’язуються за допомогою цього методу.
Задача 1: знайти двозначне число, яке дорівнює подвоєному добутку його цифр.
Розв’язання:
Позначимо шукане двозначне число через
(риска над значенням числа, що записане за допомогою цифр 
та 
, ставиться для того, щоб відрізнити цей запис від запису добутку 
). Так як число містить десятків і одиниць, то: 
.За умовою задачі :
або 
.Звідки
.Враховуючи, що
та - цифри 
, шуканий результат можна отримати за допомогою повного перебору усіх можливих значень , тобто у останню рівність треба просто послідовно підставити замість значення . Виконавши підстанови, впевнюємося, що лише одне значення 
задовольняє рівність. В цьому випадку , тобто: 
.Відповідь : шукане число 36.
Отже, метод повного перебору полягає в наступному: у рівняння треба підставити послідовно усі можливі значення невідомих і вибрати ті, що дають цілі розв’язки рівняння.
Після розгляду задачі 1 слід розглянути більш складну задачу, пов’язану із повним перебором.
Задача 2: Знайти усі двозначні числа, кожне з яких на 9 більше суми квадратів його цифр.
Розв’язання: Позначимо шукане двозначне число через
. Тоді за умовою задачі:
або 
( , - цифри).Перепишемо це рівняння у вигляді:
Вважаємо, що це квадратне рівняння відносно
. Воно буде мати розв’язок тільки при невід’ємному дискримінанті:
при умові 
Розв’язуючи цю нерівність, отримуємо:
Цій умові задовольняють лише цифри
.Цю нерівність розв’язувати зовсім необов’язково, можна просто перевірити, що із всіх цифр цій нерівності задовольняють лише цифри
.Розглянемо, чи має це рівняння розв’язки в цілих числах при таких значеннях
:При
рівняння має вигляд: 
Тоді
; 
, тобто умові задачі задовольняють числа 10 і 90.При
рівняння має вигляд: Тоді
; , тобто умові задачі задовольняють числа 11 і 91.При
рівняння має вигляд: 
Тоді
, тобто в цьому випадку рівняння не має розв’язків в цілих числах. При
рівняння має вигляд: 
Тоді
і в цьому випадку рівняння не має розв’язків в цілих числах. При
рівняння має вигляд: 
Тоді
; 
, тобто умові задачі задовольняють числа 34 і 74.Відповідь: шукані двозначні числа: 10, 11, 34, 74, 90, 91.
Дослідження цього рівняння можна організувати іншим способом:
Перепишемо це рівняння у вигляді:
Послідовно підставляємо замість
значення: .При
: 
; 
; ; ;При
: ; ; ; ;При
: 
; 
- не має цілих значень.При
: 
; 
- не має цілих значень.При
: 
; 
;
; 
;При
значення виразу 
, тобто рівняння не має дійсних розв’язків.Учням треба показати обидва способи, і обов’язково зробити висновок про раціональність.
Домашнє завдання:
Задача 3: Два двоцифрові числа 46 і 96 мають цікаву особливість: їх добуток не змінює величину, якщо цифри чисел переставити.
Дійсно,
. Треба з’ясувати чи існують ще інші пари двозначних чисел з аналогічною властивістю. Як відшукати їх всі?Розв’язання:
Позначимо цифри шуканих чисел через
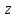і , 
і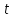 
. Складемо рівняння:
Розкриваємо дужки та спрощуємо:
, де , , , 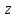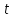- цілі числа 
.Для пошуку розв’язків складаємо із 9 цифр усі пари із рівними добутками.
Прибравши всі добутки, вибираємо тільки потрібні:
Усього рівностей 9. Із кожної можна скласти одну або дві шукані групи чисел. Наприклад, із рівності
складаємо одне рішення:
Із рівності
знаходимо два рішення:
, 
Таким чином відшукуємо наступні 14 розв’язків :
Відповідь: Пари двоцифрових чисел, добуток яких не змінюється при перестановці цифр чисел, наступні 12 і 42, 12 і 36, 12 і 84, 13 і 62, 13 і 93, 14 і 82, 23 і 64, 23 і 96, 24 і 63, 24 і 84, 26 і 93, 34 і 86, 36 і 84, 46 і 96.
Цій приклад треба почати на уроці: розібрати умову задачі, скласти рівняння, розглянути ідею розв’язування, а вже громіздкі обчислення та безпосередній перебір залишити додому.
1 2 3 4 5