
Ім'я файлу: КУРСОВА РОБОТА.docx
Розширення: docx
Розмір: 73кб.
Дата: 30.05.2021
скачати
Пов'язані файли:
Оператори проектування.doc
Розширення: docx
Розмір: 73кб.
Дата: 30.05.2021
скачати
Пов'язані файли:
Оператори проектування.doc
Київський національний університет імені Тараса Шевченка
Факультет комп’ютерних наук та кібернетики
Кафедра дослідження операцій
КУРСОВА РОБОТА
на тему:
Зображення скінченних груп
Науковий керівник:
Доктор фіз.-мат. наук
Проскурін Данило Павлович
Роботу виконав:
Студент 3-го курсу
Балашов Олександр Сергійович
КИЇВ 2021
ЗМІСТ
1.ВСТУП 3
2.ЗАГАЛЬНІ ВІДОМОСТІ ПРО ЗОБРАЖЕННЯ ГРУПИ 4
2.1Означення 4
2.2Приклади лінійних зображень 6
2.3Підзображення 7
2.4Незвідні зображення 9
2.5Тензорний добуток двох зображень 10
3.ТЕОРІЯ ХАРАКТЕРІВ 13
3.1Характер зображення 13
2.6Перші твердження Леми Шури 15
2.7Відношення ортогональності для характерів 19
4.ВИСНОВОК 22
5.Список використаної літератури 23
ВСТУП
Зображення груп – є одним із найважливіших розділів в торії груп, та, в той же час, одним з найбільш прикладних знарядь, що використовуються в дослідженнях цієї дисципліни. Вони мають численні застосування в різноманітних галузях людської життєдіяльності, а саме, широко використовуються в таких науках, як геометрія, фізика, хімія і, навіть, кристалографія. Таким чином розділ абстрактної математики, має багато практичних застосунків. Базу для яких буде розглянуто в даній роботі.
ЗАГАЛЬНІ ВІДОМОСТІ ПРО ЗОБРАЖЕННЯ ГРУПИ
Означення
Нехай
 - векторний простір над полем комплексних чисел
- векторний простір над полем комплексних чисел 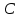 . Нехай, покладемо, що
. Нехай, покладемо, що 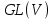 - група його автоморфізмів над тим же полем. Тоді кожен елемент групи
- група його автоморфізмів над тим же полем. Тоді кожен елемент групи 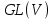 , за означенням, є таким лінійним відображенням (позначимо його
, за означенням, є таким лінійним відображенням (позначимо його 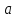 ), простору
), простору  в себе що для кожного такого відображення існує зворотне
в себе що для кожного такого відображення існує зворотне 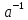 , котре також є лінійним. В випадку наявності у простору
, котре також є лінійним. В випадку наявності у простору  скінченного базису із
скінченного базису із 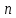 елементів
елементів 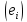 , будь яке лінійне відображення
, будь яке лінійне відображення 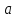 :
: 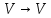 задається квадратною матрицею
задається квадратною матрицею 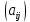 порядку
порядку 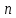 . Коефіцієнти
. Коефіцієнти 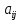 – комплексні числа, що з’являються при розкладі векторів
– комплексні числа, що з’являються при розкладі векторів 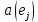 по базису
по базису 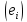 :.
:. 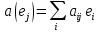 | (1) |
При цьому відображення
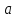 – ізоморфне тоді і тільки тоді, коли визначник
– ізоморфне тоді і тільки тоді, коли визначник 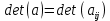 – не нульовий. У випадку виконання вищезазначених умов, отримуємо, що група
– не нульовий. У випадку виконання вищезазначених умов, отримуємо, що група 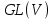 – тотожна групі оборотних квадратних матриць порядку
– тотожна групі оборотних квадратних матриць порядку 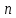 .
.Нехай тепер
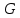 - деяка кінцева група. Лінійним зображенням групи
- деяка кінцева група. Лінійним зображенням групи 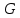 в просторі
в просторі  називається довільний гомоморфізм
називається довільний гомоморфізм 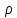 групи
групи 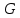 в групу
в групу 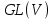 . Інакше кажучи, це таке співвідношення, де кожний елемент
. Інакше кажучи, це таке співвідношення, де кожний елемент 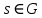 співставляеться елементу
співставляеться елементу 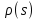 групи
групи 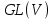 , так, що має місце рівність:
, так, що має місце рівність: 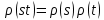 для всіх для всіх 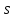 , ,  . . | (2) |
(Надалі іноді позначатимемо
 , як
, як 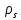 )
)Зауважимо, що з попередньої рівності випливає:
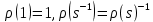 . . | (3) |
При заздалегідь заданому
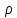 простір
простір  називається зображенням групи
називається зображенням групи 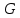 . Також одразу зауважимо, що надалі будем завжди використовувати випадок, при якому
. Також одразу зауважимо, що надалі будем завжди використовувати випадок, при якому  – буде мати скінченну розмірність. Таке обмеження має право на існування, адже в більшості випадків, як правило, нас цікавить саме поведінка скінченної кількості елементів
– буде мати скінченну розмірність. Таке обмеження має право на існування, адже в більшості випадків, як правило, нас цікавить саме поведінка скінченної кількості елементів 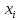 , простору
, простору  . Також зауважимо, що завжди можна знайти підзображення скінченної розмірності, що буде містити елементи
. Також зауважимо, що завжди можна знайти підзображення скінченної розмірності, що буде містити елементи 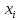 , якщо взяти підпростір простору
, якщо взяти підпростір простору  , котре породжене образами
, котре породжене образами 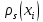 елементів
елементів 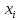 .
.Також будемо вважати, виходячи з попередніх тверджень, що що простір
 – скінченновимірний, з розмірністю
– скінченновимірний, з розмірністю 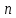 . Тоді число
. Тоді число 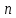 будемо називати також степенем зображення, що розглядається. Нехай
будемо називати також степенем зображення, що розглядається. Нехай 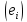 – деякий базис простору
– деякий базис простору 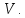 За
За  позначимо матрицю автоморфізму
позначимо матрицю автоморфізму 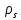 відносно даного базису. Тоді:
відносно даного базису. Тоді: 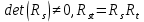 , , 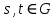 . . | (4) |
Якщо через
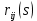 позначимо коефіцієнти матриці
позначимо коефіцієнти матриці  , то формула (2) перетвориться на:
, то формула (2) перетвориться на: 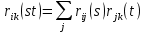 | (5) |
І навпаки, задання деяких оборотних матриць
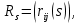 що задовільнять попереднім тотожностям, задає певне лінійне зображення
що задовільнять попереднім тотожностям, задає певне лінійне зображення 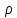 групи
групи 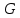 в просторі
в просторі  . Інакше кажучи задає лінійне зображення в матричній формі.
. Інакше кажучи задає лінійне зображення в матричній формі.Нехай
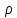 та
та 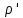 - два лінійних зображення групи
- два лінійних зображення групи 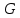 в просторах
в просторах  та
та 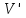 відповідно. Кажуть що зображення
відповідно. Кажуть що зображення 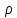 та
та 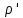 - подібні (еквівалентні чи ізоморфні), якщо існує такий лінійний ізоморфізм
- подібні (еквівалентні чи ізоморфні), якщо існує такий лінійний ізоморфізм 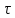 :
: 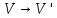 , який переводить зображення
, який переводить зображення 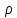 в
в 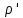 , інакше кажучи, котрі задовольняють наступній умові:
, інакше кажучи, котрі задовольняють наступній умові:  , для будь-якого , для будь-якого 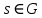 . . | (6) |
В випадку коли зображення
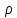 та
та 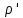 , заданні в метричній формі, як, відповідно,
, заданні в метричній формі, як, відповідно,  і
і 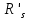 – це еквівалентно існуванню такої оборотної матриці
– це еквівалентно існуванню такої оборотної матриці 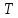 , що:
, що: 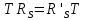 , або , або 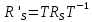 , для всіх , для всіх 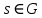 . . | (7) |
Помітимо, що такі зображення можна ототожнювати. Наприклад, поставивши у відповідність кожному елементу
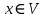 елемент
елемент 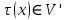 . Зокрема, вони мають одну і ту ж ступінь
. Зокрема, вони мають одну і ту ж ступінь