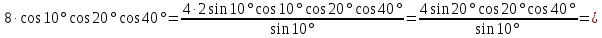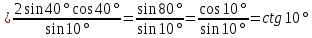Ім'я файлу: Метод доведення від супротивного.docx
Розширення: docx
Розмір: 37кб.
Дата: 09.05.2021
скачати



Теоретичні основи доведення методом від супротивного


Теорема.Побудоватеореми.У математиці теоремою називають будь-яке твердження, що має доведення його істинності. Означене поняття характеризується двома основними ознаками:

  1. Теорема - це існування твердження (правильного, справедливого). Нагадаємо, що твердженням у логіці називається речення, яке може бути істинним або хибним. При цьому важливу роль відіграють наступні логічні закони:

  • закон виключення третього: будь-яке висловлювання може бути або істинним, або хибним (нічого третього бути не може);

  • законнесуперечності:ніяке висловлювання не може бути одночасно і істинним, і хибним.

Речення, в якому неможливо одночасно визначити, істинне воно чи хибне, не є твердженням.

  1. Істинність теореми визначається за допомогою доведення - спеціального роздуму, що склада­ ється з ланцюжка правильних висновків.

Твердження без доведення (навіть коли воно істинне) не є теоремою.

У шкільній математиці прийнято розрізняти теореми двох типів. До першого з них відносяться теореми з наступною суттю: "Якщо А, то В", де А і В - деякі твердження. У цьому висловлюванні А називається умовою, а В - висновком теореми.

До другого типу відносяться так звані теореми існування, що тракгуються наступним чином: "Існує об'єкт, який володіє даною властивістю Р". У таких теоремах виділити умову і висновок неможливо.

Досвід засвідчує: учні не завжди чітко розумі­ ють, що, зазвичай, стверджує теорема "Якщо А, то В", тому нерідко припускаються грубих помилок. У теоремі "Якщо А, то В" йдеться про те, що:

    1. щоразу, коли виконується умова А, обов'язково істинним є і висновок В;

    2. якщо умова А не виконується, то про істинність висновку В нічого сказати не можна (він може бути не лише істинним, а й хибним).

Приклад 1. Наведемо найбільш типові помилки, які допускають учні. Знаючи, що в прямокутнику діагоналі рівні, вони нерідко вважають, що якщо чотирикутник не є прямокутником, то його діагоналі нерівні між собою; з теореми "Якщо дві паралельні площини перетнути третьою, то прямі їх перетину не є паралельними і т. д.

Прямедоведеннятеореми.Розрізняють два види доведення: пряме і непряме. Прямим назива­ ється доведення, коли воно є ланцюжком послідовно зв'язаних висновків, що безпосередньо ведуть від умови теореми до висновку (або від аксіоми і раніше доведених теорем до даної теореми).

Приклад 2. Довести, що якщо а+ b+ с= 0,то а3+ b3+ с3= Заbс.

Доведення. За умовою а + b+ с = 0, тому а+ b= - с,

звідси - (а+ b)3= -с3або а3+ b3+ Заb(а+ b)= -с3,а3+ b3 - Заbс= -с3;

таким чином доведено, що а3+ b3+ с3= Заbс

Приклад З. Довести справедливість рівності 8cosl0° cos20° cos40° = ctg10°.
Доведення.



Непрямі доведення. Розглянемо суть непрямого доведення. Нехай потрібно довести деяку теорему. Замість цього ми доводимо інше твердження, яке пов'язане з даним так, що з отриманого результату обов'язково випливає істинність означеної теореми. Більшість шкільних теорем доводяться непрямим методом, що викликає значні труднощі у вивченні математики.

Приклад 4. На стороні ADі на діагоналі АСпаралелограма взято точки Мі Nтаким чином, що АМ= 1/5 AD,AN= 1/6 АС.Доведіть, що точки В, М,Nналежать одній прямій.

Доведення.



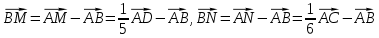
Звідси отримаємо, що

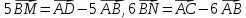
віднімемо від пер шого рівняння друге:



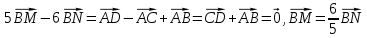
Тобто вектори 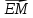і 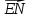колінеарні і точки Е,М, Nлежать на одній прямій.

Більша частина роздумів щодо вищеозначеного присвячена доведенню не того твердження, що подане в задачі, а обrрунтуванню колінеарності векгорів 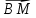і 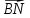.Із цього результату потім легко виводиться потрібне.

Запереченнятвердження.Маючи деяке висловлювання Т,на його основі завжди можна скласти нове - “Неправильно, що Т”.Якщо висловлювання Т є істинним, то нове висловлювання буде хибним і навпаки. Висловлювання “Неправильно, що Т”позначається 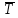і називається запереченням висловлювання T.

Зазвичай запереченням твердження Тназивається також висловлювання Т,яке хибне, коли дане висловлювання істинне, та істинне, коли воно хибне.

Очевидно, що твердження Т, у свою чергу, є запереченням для 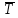, тобто твердження 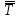(заперечення заперечення) рівносильне вихідному твердженню Т (закон заперечення заперечення).

Описаний вище спосіб отримання заперечення, що називається зовнішнім, має серйозний недолік, адже із завданням у такій формі досить незручно працювати. Тому в математиці використовують інші, більш складні, але практичніші способи побудови заперечень (їх ще називають внутрішніми).

Приклад 5. Розглянемо твердження про те, що в будь-якому випуклому чотирикутнику сума діагона лей не менша від суми його сторін. Це висловлювання неправильне, тому його заперечення є істинним. Побудуємо заперечення спочатку зовнішнім способом: "Неправильно, що в будь-якому випуклому чотирикутнику сума діагоналей менша від суми сторін".

Заперечення, задане внутрішнім способом, формулюється наступним чином: «Існує хоча б один чотирикутник, в якого сума діагоналей менша за суму сторін».

Отже, при внутрішньому запереченні відбува­ ється значна перебудова всього речення, виконати яку, звичайно, набагато складніше, ніж механічно прикріпити слова "неправильно, що...”. Однак переваги цього заперечення досить очевидні, адже з таким завданням значно зручніше проводити подальшу роботу.

Яким же чином будуються внутрішні заперечення? Із цією метою учням буде достатньо зрозуміти і засвоїти два основні правила.
Правило №1



Твердження
Його заперечення

  1. Усі дані об'єкти володіють однією і тією ж властивістю Р.

  2. Випадковість: об'єкти А або В володіють властивістю Р.

  1. Хоча б один із даних об'єктів не володіє властивістю Р або існує хоча б один такий об’єкт, який не володіє властивістю Р.

  2. Об' єкти А і в не володіють властивістю P.

Правило №2

Твердження
Його заперечення

1. Деякі з даних об' єктів володіють властивістю Р або існує хоча б один об'єкт, що володіє властивістю Р.

2. Випадковість: хоча б один з об’єктів А або В володіє властивістю Р.
1. Усі дані об'єкти не володіють властивістю Р.

2. Об' єкти А і В не володіють властивістю P.


Несуміснетвердження.У математиці часто доводиться мати справу з логічними несумісними твердженнями, тому необхідно розрізняти два типи несумісності.

      1. Суперечливістьтвердження. Логіка визначає це поняття наступним чином: «Два твердження називаються суперечливими, якщо вони не можуть бути одночасно ні істинними , ні хибними ».

Отже, при істинності одного з них інше завжди буде хибним і, навпаки, при хибності одного, інше - істинне.

Найважливіший випадок такого типу ми вже розглядали: будь-яке твердження Т і його заперечення є логічно суперечливими.

Протилежнітвердження. Два твердження називаються супротивними, якщо не можуть бути одночасно істинними, але можуть бути одночасно хибними.

Загалом, для твердження типу "Якщо А, то В" дуже легко створити протилежне, що визначається як "Якщо А, то не В".

Зауваження. Термін «протилежне твердження» досить невдалий, адже використовується в елемен­ тарній математиці не лише у вказаному виді, але й в іншому змісті. Досить часто для твердження "Якщо А, то В" протилежним називають твердження "Якщо А, то не В". Щоб запобігти двозначності, протилежність у змісті в логіці називають контрарністю.

Якщо ми зустрічаємося з парою логічно несумісних тверджень, то сприймаємо цей факт як прояв суперечності, що свідчить про те, що хоча б одне із вказаних тверджень хибне.

Помилковим є висновок про те, що в будь-якому випадку одне із тверджень є істинним. Це істинно, якщо наша пара тверджень суперечлива, і хибно, якщо твердження контрарні.

У результаті розглянемо три твердження:

  1. Якщо пряма перетинає графік функції, то вона не є дотичною до даного графіка.

  2. Якщо пряма перетинає графік функції, то вона є дотичною до даного графіка.

З. Існує лише один випадок, коли пряма, що перетинає графік функції, є дотичною до даного графіка.

Твердження 1 і 2 - контрарні і тому не можуть бути одночасно істинними. Звідси слідує, що або одне з них, або обидва - хибні (у даному випадку обидва є хибними).

Твердження 1 і З - суперечливі, тому можна вважати, що одне із них є істинним, а інше - хибним.

Усе сказане в логіці визначається у вигляді двох законів правильного мислення.

Законнесуперечності.Два несумісні твердження не можуть бути одночасно істинними, адже хоча б одне із них - хибне.

Закон виключення третього. Два суперечливих твердження не можуть бути одночасно хибними, одне з них обов'язково є істинним.

Спростування.На практиці часто доводиться мати справу із твердженнями, істинність яких сумнівна - гіпотезами.

Якщо гіпотезу вдається довести, то вона перетворюється в теорему. Нерідко гіпотези виявляються хибними. Доведення хибності деякого твердження називається його спростуванням.

У шкільній математиці використовують два основні способи спростування.

Спосіб 1. Щоб впевнитися в тому, що твердження "Якщо А, то В" - хибне, достатньо привести хоча б один випадок, який демонструє, що А виконується, а В - ні. Це зображення і називається контрприкладом.

Спосіб 2. Сутність цього способу полягає в наступному. Нехай дана деяка гіпотеза, яку ми хочемо спростувати. Для цього ми тимчасово вважаємо її істинною і робимо висновок, що випливає з означеного факту. Якщо вдасться зробити висновок, логічно несумісний із деяким істинним твердженням, то це означатиме, що гіпотеза неправильна.

Доведення методом від супротивного

Ідея цього методу є досить простою. Якщо потрібно довести деяку теорему Т, то замість неї ми можемо сформулювати заперечення Т і спростувати його. Зважаючи на те, що із двох тверджень Т і 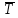одне є істинним, спростування твердження 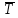є одночасно доведенням теореми Т.
Класична схема доведення методом від супротивного

У шкільній практиці учням подається наступна таблиця доведення теорем способом від супротивного.

Сутність способу доведення від супротивного:

1.
Робимо припущення, суперечливе тому, що потрібно довести.

2.
З'ясуємо, що слідує із зробленого припущення на основі аксіом, попередніх теорем і означень.

З.
Встановлюється логічна несумісність між тим, що отримали, і тим, що відомо з умови даної теореми, з аксіом, означень або раніше доведених теорем.

4.
Висновок: припущення є неправильним, правильне те, що потрібно було довести.


Такий порядок роздумів називається класичною схемою, адже добре відомий учителю і широко використовується на уроках математики. Неважко зрозуміти, що в цілому означені припущення лише за формою відрізняються від схеми попереднього пункту.

Недолікикласичноїсхеми. Використання класичної схеми доведення методом від супротивного приховує в собі два серйозні недоліки, які вчитель завжди повинен враховувати в роботі.

Перший із них полягає в тому, що учні, запам'ятавши алгоритм роботи, перестають розуміти логічну сутність доведення. Воно для них перетворюється в формальну процедуру, яка не має чіткого логічного смислу.

Не менш важливим є другий недолік, пов'язаний із першим пунктом класичної схеми.
Некласичні схеми доведення способом від супротивного

У математичній практиці використовується певний ряд схем міркувань, які за своєю логічною природою рівносильні розглянутим вище схемам доведення від супротивного. Вчителю корисно знати ці схеми, вони нерідко зустрічаються в науковій і навчальній літературі.

Під час аналізу матеріалу ми використовуємо елементи математичної логіки.

Важливим також для учнів є вміння створювати заперечення для твердження виду "Якщо А, то В". Усе це робиться на основі наступних простих роздумів. Кожне висловлювання виду "Якщо А, то В" стверджує, що в усіх випадках, коли виконується умова А, обов' язково повинен виконуватися і висновок В. У зв' язку з цим заперечення може бути сформульовано наступним чином: "Існує хоча б один випадок, коли умова А виконується, а висновок В - ні".
скачати

© Усі права захищені
написати до нас