
ІІ задача динаміки
| Дано: | 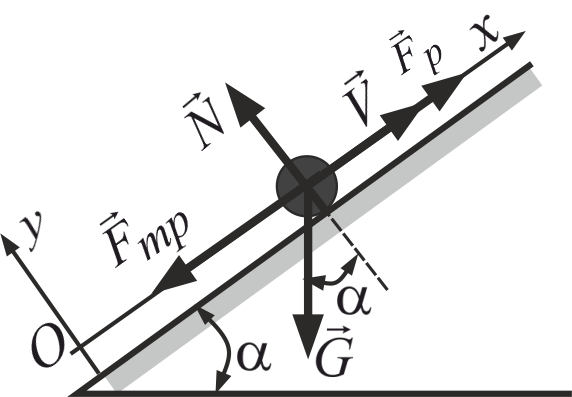 |
| Знайти: |
Розв’язання: Основний закон динаміки (ІІ закон Ньютона):
У диференціальному вигляді:
Обираємо систему координат (вісь Ох спрямовуємо вздовж швидкості). В точці О – початкове положення точки. В проекціях на вісі координат:
З другого рівняння:
Диференціальне рівняння руху запишемо у вигляді:
Розв’язуємо методом розділення змінних. Ділимо на масу m обидві частини:
Замість рушійної сили підставляємо задану функцію:
домножаємо на dt праву та ліву частини:
Інтегруємо:
Отримуємо:
Оскільки
Розділяємо змінні (домножаємо на
Отримуємо:
Невідомі сталі інтегрування
Остаточно маємо:
ІІ задача динаміки
| Дано: | 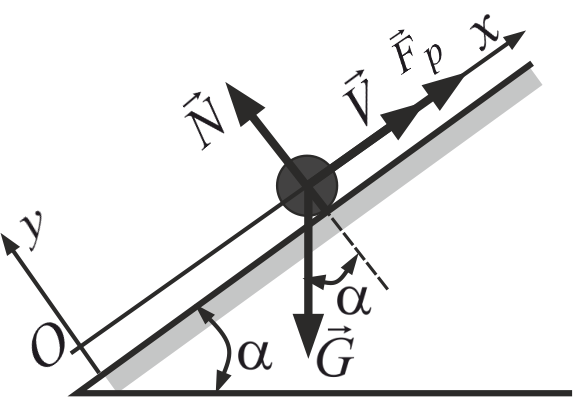 |
| Знайти: |
Розв’язання: Основний закон динаміки (ІІ закон Ньютона):
У диференціальному вигляді:
Обираємо систему координат (вісь Ох спрямовуємо вздовж швидкості). В точці О – початкове положення точки. В проекціях на вісі координат:
З другого рівняння:
Диференціальне рівняння руху запишемо у вигляді:
Розв’язуємо методом розділення змінних. Ділимо на масу m обидві частини:
Замість рушійної сили підставляємо задану функцію:
домножаємо на dt праву та ліву частини:
Інтегруємо:
Отримуємо:
Оскільки
Розділяємо змінні (домножаємо на
Отримуємо:
Невідомі сталі інтегрування
Остаточно маємо:
ІІ задача динаміки
| Дано: | 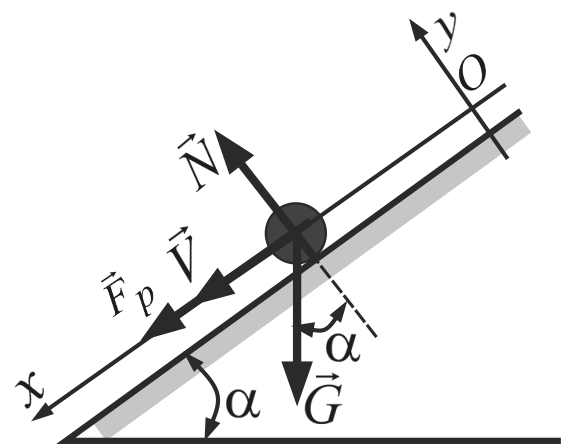 |
| Знайти: |
Розв’язання: Основний закон динаміки (ІІ закон Ньютона):
У диференціальному вигляді:
Обираємо систему координат (вісь Ох спрямовуємо вздовж швидкості). В точці О – початкове положення точки. В проекціях на вісі координат:
З другого рівняння:
Диференціальне рівняння руху запишемо у вигляді:
Розв’язуємо методом розділення змінних. Ділимо на масу m обидві частини:
Замість рушійної сили підставляємо задану функцію:
домножаємо на dt праву та ліву частини:
Інтегруємо:
Отримуємо:
Оскільки
Розділяємо змінні (домножаємо на
Отримуємо:
Невідомі сталі інтегрування
Остаточно маємо:
ІІ задача динаміки
| Дано: | 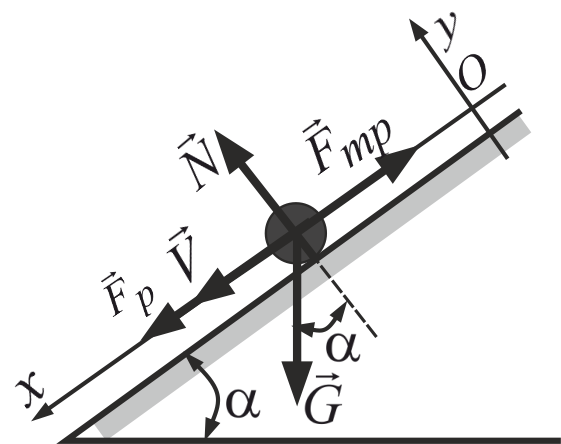 |
| Знайти: |
Розв’язання: Основний закон динаміки (ІІ закон Ньютона):
У диференціальному вигляді:
Обираємо систему координат (вісь Ох спрямовуємо вздовж швидкості). В точці О – початкове положення точки. В проекціях на вісі координат:
З другого рівняння:
Диференціальне рівняння руху запишемо у вигляді:
Розв’язуємо методом розділення змінних. Ділимо на масу m обидві частини:
Замість рушійної сили підставляємо задану функцію:
домножаємо на dt праву та ліву частини:
Інтегруємо:
Отримуємо:
Оскільки
Розділяємо змінні (домножаємо на
Отримуємо:
Невідомі сталі інтегрування
Остаточно маємо: