Задачі до теми 1
Задача 1.1 Позика в розмірі 15000 грн. видана 1 березня до 5 грудня під 28% річних (рік високосний). Визначити розмір нарощеної суми для різних варіантів (звичайного і точного) розрахунку відсотків.
Розв’язання.
Попередньо ми визначили, що точна кількість днів становить 280, а наближена – 277.
Для кожного із методів маємо відповідно:
1) К = 366, t = 280. S 15000 (1
0.28) 18 213 11 грн. 2) К = 360, t = 280. S 15000 (1
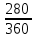0.28) 18 266 66 грн. 3) К = 360, t = 277. S 15000 (1+
0.28) = 18 231 66 грн.Отже, як бачимо, ми отримали різні фінансові результати угоди в залежності від вибору часової бази і методу розрахунку кількості днів.
Задача 1.2 Позика в розмірі 27000 грн. видається на 4 роки. Ставка відсотків за перший рік - 35%, а за кожне наступне півріччя вона зменшується на 2%. Визначити множник нарощення і нарощену суму.
Розв’язання.
Множник нарощення становить:
1 +
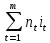= 1 + 
× 0.35 + × 0.2 + × 0.25 + × 0.3 = а накопичена на рахунку за рік сума складе:
S 27000 1. 2125 32 738 грн.
У фінансових операціях з короткотерміновими депозитами часто використовують повторне інвестування коштів, тобто відбувається багаторазове нарощення відсоткового доходу, яке називається реінвестуванням, або капіталізацією.
Задача 1.3 Визначити період нарахування, за який початковий капітал у розмірі 18000 грн. зросте до 43000 грн., якщо використовується проста ставка відсотків 31% річних?
Розв’язання
Pn = P(1 + r n); n =
; n = 
= 2.4 р.Задача 1.4 Визначити просту ставку позичкових відсотків, при якій початковий капітал у розмірі 13000 грн. досягне 18000 грн. через рік.
Розв’язання
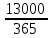= 36%Задача 1.5 Позика видається під просту ставку позичкових відсотків 30% річних на 235 днів. Розрахувати суму, одержувану позичальником і суму відсоткових грошей, якщо треба повернути 75000 грн.
Розв’язання:
S =
= 
= 48 400 грн.Задача 1.6 Позика в розмірі 3600 грн. видається на 500 днів під просту ставку позичкових відсотків 36% річних. Визначити суму відсоткових грошей і суму, що повинна бути повернута.
Величина боргу разом з нарахованими відсотками згідно виразу становить:
S = 3600 ( 1 +3 × 0.36) = 7 488 грн.
n =
= 1.4S = 3600 (1+ 0.36) × (1+1.4×0.36) = 4896 ×1.504 = 7364 грн.
Задача 1.7 Розрахувати суму грошових коштів, яку необхідно вкласти до банку „сьогодні", якщо депозитна ставка складає 20% річних для того, щоб: а) через 4 роки на рахунку у банку було 20 тис. грн.. б) через 3 роки на рахунку у банку було 25 тис. грн.. в) через 5 років на рахунку у банку було 30 тис. грн.
Розв’язання:
а) PV=20000·1/((1+0,2·4))=11111,1
б) PV=25000·1/((1+0,2·3) )=15625
в) PV=30000·1/((1+0,2·5))=15000
Задача 1.8 Дати оцінку рішенню інвестора. Інвестор має вільні грошові кошти у розмірі: а) 1223 тис. грн. б) 683 тис. грн. в) 500 тис. грн. Чи зможе він придбати обладнання А вартістю 1200 тис. грн. через 2 роки та обладнання Б вартістю 700 тис. грн. через 4 роки, якщо „сьогодні" інвестує кошти до банку під 10% річних?
Задача 1.9 Визначити майбутню вартість інвестицій, якщо: а) термін вкладу складає 3 роки, ставка відсотку за депозитом - 18% річних; б) термін вкладу складає 5 років, ставка відсотку за депозитом - 20% річних; в) термін вкладу складає 6 років, ставка відсотку за депозитом - 30% річних Фірма укладає до банку на депозит грошову суму у розмірі 850 тис. грн.
Задача 1.10 Компанія аналізує доцільність вкладення у її розвиток $15000 власних коштів на умовах, що через 2 роки вони повинні принести $20000. При цьому компанія хоче мати річний доход не менш 10%. Чи реальні такі умови? Проаналізуйте усі можливі варіанти.