
Для градієнта знайдено розв’язання в точці
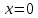 отримуємо значення
отримуємо значення 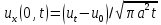 . Прирівнюючи його експериментально встановленому значенню термічного градієнта біля поверхні Землі
. Прирівнюючи його експериментально встановленому значенню термічного градієнта біля поверхні Землі 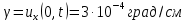 , приходимо до рівності
, приходимо до рівності  , що містить початкову температуру u, температуру схолонувши за час t, поверхні
, що містить початкову температуру u, температуру схолонувши за час t, поверхні  , коефіцієнт температуропровідності
, коефіцієнт температуропровідності 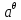 і сам час відшукання t1 першочергово розжареної до температури u1 Землі. Підставляючи в цю рівність значення
і сам час відшукання t1 першочергово розжареної до температури u1 Землі. Підставляючи в цю рівність значення 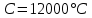 (температура плавлення горних порід),
(температура плавлення горних порід), 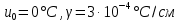 , а також значення
, а також значення  , що відповідає середньому експериментальному оприділяючому коефіцієнту температуропровідності, отримаємо для продовження процесу охолодження Землі значення
, що відповідає середньому експериментальному оприділяючому коефіцієнту температуропровідності, отримаємо для продовження процесу охолодження Землі значення  . Таке представлення про вік Землі не погоджується з геологічними даними:
. Таке представлення про вік Землі не погоджується з геологічними даними:  . До останнього значення можна наблизитися, уточнюючи математичну модель охолодження Землі безпосередньо введенням в рівняння (110) джерел тепла, обумовлених радіоактивним розпадом [4]. Однак для такої точної задачі важко використовувати перетворення Больцмана.
. До останнього значення можна наблизитися, уточнюючи математичну модель охолодження Землі безпосередньо введенням в рівняння (110) джерел тепла, обумовлених радіоактивним розпадом [4]. Однак для такої точної задачі важко використовувати перетворення Больцмана.Повертаючись до крайової задачі для нелінійного рівняння (109), відмітимо, що функція
 в тих випадках, коли її не вдається знайти аналітично, може бути знайдена за допомогою чисельного інтегрування. Розглянемо в якості прикладу, випадок лінійної залежності
в тих випадках, коли її не вдається знайти аналітично, може бути знайдена за допомогою чисельного інтегрування. Розглянемо в якості прикладу, випадок лінійної залежності 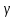 від u:
від u: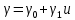 . Початково-краєва задача про розігрів на півпростору з такою залежністю коефіцієнта теплопровідності від температури записується у вигляді:
. Початково-краєва задача про розігрів на півпростору з такою залежністю коефіцієнта теплопровідності від температури записується у вигляді:
де
 – постійний коефіцієнт температуропровідності. Після попередньої зміни масштабу часу
– постійний коефіцієнт температуропровідності. Після попередньої зміни масштабу часу  і шкала значень температури
і шкала значень температури  перетворення Больцмана
перетворення Больцмана  , трансформує початково-краєву задачу (115) в доточкову краєву задачу
, трансформує початково-краєву задачу (115) в доточкову краєву задачу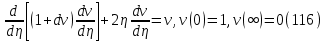
відносно функції
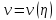 .
.На рисунку12.2 наведено результати чисельного розв’язання цієї кураєвої задачі для різних значень параметра
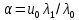 [I].
[I].2. Загальне перетворення подібності
В ряді випадків для нелінійного диференціального рівняння часткових похідних з двома незалежними змінними
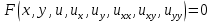 (117)
(117)вдається отримати сім’ю розв’язків способом приведення їх до звичайних диференціальних рівнянь за допомогою одночасного перетворення незалежних до залежних змінних:
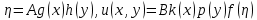 (118)
(118)Тут А і В – довільні постійні, а g, h, k, p i f – функції, підібрані як розв’язок нелінійних диференціальних рівнянь. Розглянуте вище перетворення Больцманає частковим випадком такого перетворення
 . Нарівні з перетворенням незалежних змінних це перетворення включає також розділення змінних. На прикладі квазілінійного рівняння теплопровідності ми бачили, як перетворення Больцмана трансформує рівняння в частинні похідні і в звичайне нелінійне диференціальне рівняння. Нижче розглянемо випадки, коли загальне перетворення подібності (118) дозволяє досягнути такої ж мети.
. Нарівні з перетворенням незалежних змінних це перетворення включає також розділення змінних. На прикладі квазілінійного рівняння теплопровідності ми бачили, як перетворення Больцмана трансформує рівняння в частинні похідні і в звичайне нелінійне диференціальне рівняння. Нижче розглянемо випадки, коли загальне перетворення подібності (118) дозволяє досягнути такої ж мети.а) Теплові хвилі
При випромінюванні високотемпературних процесів необхідно враховувати залежність коефіцієнтів теплоємності і теплопровідності від температури. Потужність теплових джерел можить також залежати від температури, якщо наприклад, тепло виділяється в процесі хімічної реакції. В результаті отримаємо для опису розповсюдження тепла квазілінійне рівняння теплопровідності
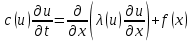 (119)
(119)де густина рідини ρ прийнята рівно.одиниці. В загальному випадку
 .
.В неоднорідному середовищі λ і с можуть бути розривними функціями аргументів x i u (для різних речей залежність λ, с від температури залежна). Рівняння виду (119) зустрічається також при вивченні проникнення магнітного поля в середовище, магнітна проникність якого залежить від магнітного поля. За допомогою спеціального функціонального перетворення рівняння (119) приводиться до одного із видів
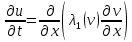 або
або  . (120)
. (120)Так, наприклад перетвореня Кіргофа
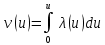 зворотне йому перетворення
зворотне йому перетворення 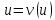 трансформує рівняння (119) в друге рівняння (120) з
трансформує рівняння (119) в друге рівняння (120) з 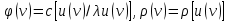 .
.Якщо коефіцієнт теплопровідності
 є степеневою функцією температури –
є степеневою функцією температури – 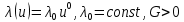 – а коефіцієнт теплопровідності с постійний, то розв’язання початково-краєвої задачі
– а коефіцієнт теплопровідності с постійний, то розв’язання початково-краєвої задачі 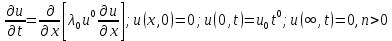 . (121)
. (121)можна отримати скориставшись загальним перетворенням подібності (118). Справді, спираючись
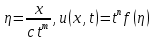 , де
, де 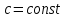 , отримуємо
, отримуємо 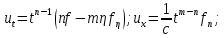
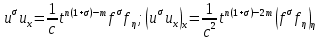 , (122)
, (122)в силу чого рівняння (121) набуває вигляду
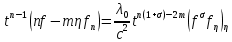 . (123)
. (123) Покладаючись в цьому рівнянні
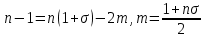 , після скорочення на
, після скорочення на  приходимо до звичайного диференціального рівняння для
приходимо до звичайного диференціального рівняння для 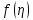 :
: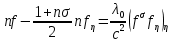 . (124)
. (124)Дане рівняння потрібно інтегрувати при краєвих умовах
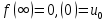 , що витікають із початково-краєвих умов (121) в результаті застосування розглянутого перетворення подібності. У випадку
, що витікають із початково-краєвих умов (121) в результаті застосування розглянутого перетворення подібності. У випадку 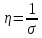 краєва задача для рівняння (124) переписується у вигляді
краєва задача для рівняння (124) переписується у вигляді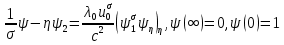 . (125)
. (125)де
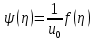 . Нарешті, покладаючи
. Нарешті, покладаючи 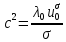 , отримаємо нелінійне рівняння другого порядку
, отримаємо нелінійне рівняння другого порядку . (126)
. (126)Розв’язок цього рівняння, задовольняє краєвій умові
 , відповідно шукати у вигляді
, відповідно шукати у вигляді 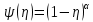 . Так як при цьому
. Так як при цьому 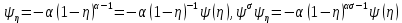 , тому, покладаючи
, тому, покладаючи 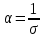 , перепишемо рівняння (126) у вигляді
, перепишемо рівняння (126) у вигляді 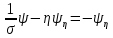 частинним розв’язком якого є
частинним розв’язком якого є  . Оскільки
. Оскільки  , то даний розв’язок, очевидний суттєво лише на інтервалі
, то даний розв’язок, очевидний суттєво лише на інтервалі 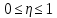 . Щоб отримати розв’язок краєвої задачі (125) на всій півосі
. Щоб отримати розв’язок краєвої задачі (125) на всій півосі  , необхідно додатково розглянути краєву задачу
, необхідно додатково розглянути краєву задачу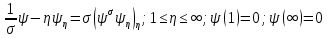 (127)
(127)з краєвою умовою
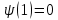 , отримуємо по неперервності із розв’язку
, отримуємо по неперервності із розв’язку 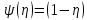 . Але в силу даної умови із диференціального рівняння (127) слідує, що
. Але в силу даної умови із диференціального рівняння (127) слідує, що 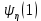 , а також всі вищі похідні
, а також всі вищі похідні 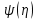 при
при  рівні нулю. Тому розв’язок
рівні нулю. Тому розв’язок  можливо бути продовжено на полу вісь
можливо бути продовжено на полу вісь 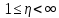 лише тотожним нулем:
лише тотожним нулем: 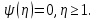
Отже, розв’язок краєвої задачі (125) має вигляд
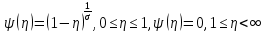 . Повертаючись до старих змінних x, t i u, отримаємо розв’язок вихідної початково-краєвої задачі (121) при
. Повертаючись до старих змінних x, t i u, отримаємо розв’язок вихідної початково-краєвої задачі (121) при  :
: (128)
(128)Даний розв’язок визначає теплову хвилю, що розповсюджується з кінечною швидкістю
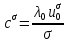 , що залежить від степені не лінійності коефіцієнта теплопровідності
, що залежить від степені не лінійності коефіцієнта теплопровідності 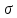 , а також величин
, а також величин  і
і 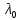 . Для значень параметрів
. Для значень параметрів 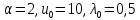 розв’язок (128) наведено на рисунку 12.3. Щвидкість розповсюдження теплової хвилі в даному випадку дорівнює 5
розв’язок (128) наведено на рисунку 12.3. Щвидкість розповсюдження теплової хвилі в даному випадку дорівнює 5 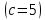 . Якщо
. Якщо 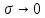 , то
, то  , рівняння (121) в границі стає лінійним, а швидкість розповсюдження теплової хвилі
, рівняння (121) в границі стає лінійним, а швидкість розповсюдження теплової хвилі 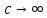 . Незвичайне для процесів розповсюдження тепла кінечне значення швидкості розповсюдження с обумовлюється виключно залежністю коефіцієнта теплопровідності λ від температури u, тобто квазілінійністю вихідного рівняння (121).
. Незвичайне для процесів розповсюдження тепла кінечне значення швидкості розповсюдження с обумовлюється виключно залежністю коефіцієнта теплопровідності λ від температури u, тобто квазілінійністю вихідного рівняння (121).в) Рівняння прикордонного слою для стаціонарної площини течії
Розглянемо встановлену течію в’язкої не закипаючої рідини над нерухомою площиною
 . Будемо вважати,що течія є плоскою, тобто компоненти швидкості n і v не залежать від координати x:
. Будемо вважати,що течія є плоскою, тобто компоненти швидкості n і v не залежать від координати x: 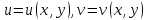 , третя компонента швидкості
, третя компонента швидкості  . Крім цього будемо припускати відомим значення швидкості течії
. Крім цього будемо припускати відомим значення швидкості течії  на достатньо великій відстані від нерухомої площини
на достатньо великій відстані від нерухомої площини 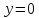 . Практично можна вважати, що
. Практично можна вважати, що 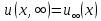 , де
, де  – відома функція x.
– відома функція x.Основні рівняння такої течії рідини складаються із одного рівняння Нав’є-Стокса і рівняння неперервності
 (129)
(129)де v – кінематична густина. Її потрібно інтегрувати при краєвих умовах
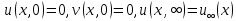 , перші два з яких виражають умову прилипання рідини до нерухомої площини
, перші два з яких виражають умову прилипання рідини до нерухомої площини 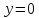 . Приведення диференціального рівняння і краєві умови слугують математичною моделлю для опису граничного слою, що виникає при обтікання тіл в одномірному направленому потоці в’язкої незжимної рідини.
. Приведення диференціального рівняння і краєві умови слугують математичною моделлю для опису граничного слою, що виникає при обтікання тіл в одномірному направленому потоці в’язкої незжимної рідини.Із введенням функції потоку
 з допомогою відношень
з допомогою відношень 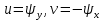 друге рівняння (129) виконується автоматично, а рівняння Нав’є-Стокса набуває вигляду
друге рівняння (129) виконується автоматично, а рівняння Нав’є-Стокса набуває вигляду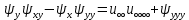 (130)
(130)Нашою першочерговою задачею є перетворення цього рівняння в звичайне диференціальне рівняння. Для цього будемо намагатися об’єднати незалежні змінні x і y одну незалежну змінну η, а також представимо шукану функцію ψ у вигляді (118).
В подальшому зручно перейти до безрозмірних величин, вводячи і розглядаючи характеристичні величини швидкості
 довжина потоку L, а також число Рейнольдца
довжина потоку L, а також число Рейнольдца 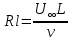 . В якості нової незалежної змінної приймемо безрозмірну величину
. В якості нової незалежної змінної приймемо безрозмірну величину 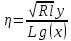 , де
, де 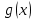 – підлягає визначенню функції. Замість x будемо розглядати безрозмірну незалежну змінну
– підлягає визначенню функції. Замість x будемо розглядати безрозмірну незалежну змінну 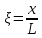 . Нарешті, залежну змінну
. Нарешті, залежну змінну  шукати у вигляді [9]
шукати у вигляді [9]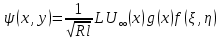 , (131)
, (131)де
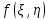 – підлягаюча визначенню функція.
– підлягаюча визначенню функція.Використовуючи представлення для η і ψ, а також
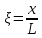 , компоненти швидкості
, компоненти швидкості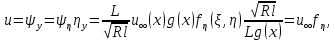
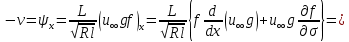 (132)
(132)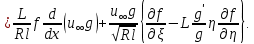
так як
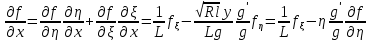 . (133)
. (133)Для другої і третьої похідної
 , що входять в рівняння (130) аналогічно отримуємо:
, що входять в рівняння (130) аналогічно отримуємо:

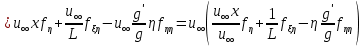 , (134)
, (134)
Підставляючи (132) – (134) в рівняння (130), отримаємо
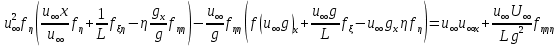
Після множення (135) на відмінний від нуля множник
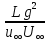 перегрупування членів остаточно отримаємо
перегрупування членів остаточно отримаємо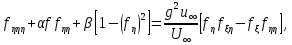 (136)
(136)де
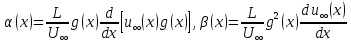 . (137)
. (137)Рівняння (136) перетворюється в звичайне диференціальне рівняння
 (138)
(138)якщо вважати, що
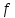 не залежить від
не залежить від 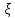 , а
, а 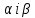 від x тобто є постійними величинами. Це означає, що
від x тобто є постійними величинами. Це означає, що 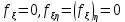 , а звідси випливає рівність нулю і права частина рівняння (136). Друга умова
, а звідси випливає рівність нулю і права частина рівняння (136). Друга умова 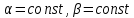 намагається задовольняти відповідним підбором що знаходяться в нашому розпорядження функцій
намагається задовольняти відповідним підбором що знаходяться в нашому розпорядження функцій 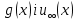 . Із (137) легко знайти що
. Із (137) легко знайти що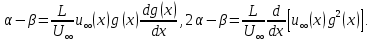 (139)
(139)Якщо
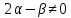 , що можливо, оскільки постійні
, що можливо, оскільки постійні 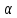 і
і  в нашому розпорядженні, то інтегруючи друге рівняння (139) і відображаючи не існуючу постійну змінну, отримуємо
в нашому розпорядженні, то інтегруючи друге рівняння (139) і відображаючи не існуючу постійну змінну, отримуємо (140)
(140)Перше рівняння (139) при цьому переписується у вигляді
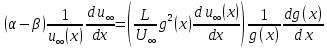 (141)
(141)Або в силу визначення
 у вигляді
у вигляді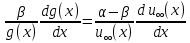 (142)
(142)Інтегруючи останнє, отримуємо
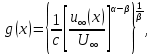 (143)
(143)Де с – стала інтегрування. Виключаючи
 із рівнянь (140) і (143), отримуємо можливий вигляд функції
із рівнянь (140) і (143), отримуємо можливий вигляд функції 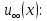
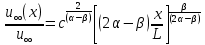 (144)
(144)при умові, що
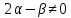 . Так як в силу (144)
. Так як в силу (144)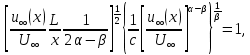 (145)
(145)то шукану функцію
 остаточно можна переписати у вигляді
остаточно можна переписати у вигляді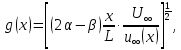 (146)
(146)де
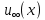 є функція вигляду (144). До визначення (146) безпосередньо приводить і відношення (140), що містить
є функція вигляду (144). До визначення (146) безпосередньо приводить і відношення (140), що містить 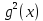 .
.Проведені обчислення дозволять завершити, що свідчення нелінійного рівняння з частковими похідними (129) до нелінійного звичайного рівняння (138) за допомогою загального перетворення подібності (131) можливо лише для степеневих функцій
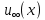 вигляду (144), що містять довільні сталі
вигляду (144), що містять довільні сталі 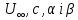 . Додатковийінтерес презентує залежність додаткової функції
. Додатковийінтерес презентує залежність додаткової функції  , що входить в перетворення (131), від характеру течії на
, що входить в перетворення (131), від характеру течії на  , тобто від
, тобто від 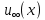 . Звісно, отримане в результаті застосування загального перетворення подібності рівняння (138) є нелінійним і відносно складним. Вперше воно було виведено В. М. Фокнером і Сільвією Скан [9] (дивіться додаткову літературу до лекції 12).
. Звісно, отримане в результаті застосування загального перетворення подібності рівняння (138) є нелінійним і відносно складним. Вперше воно було виведено В. М. Фокнером і Сільвією Скан [9] (дивіться додаткову літературу до лекції 12).Повертаючись до кураєвої задачі для рівнянь (129) - (130), відмітимо що перетворення краєвих умов для u і v краєві умови для
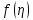 не викликає труднощів і втілюється за допомогою формул (132). Із (132), покладаючи
не викликає труднощів і втілюється за допомогою формул (132). Із (132), покладаючи  , отримуємо в силу краєвих умов для u і v, що
, отримуємо в силу краєвих умов для u і v, що  , а при
, а при 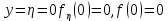 . Остаточно для визначення
. Остаточно для визначення 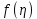 отримуємо краєву задачу
отримуємо краєву задачу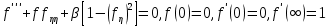 . (147)
. (147)Ця краєва задача займає одне із центральних місць в теорії прикордонного слою для стаціонарної плоскої течії. Її дослідження присвячена надзвичайно широка література [9].
Із рівнянь (137) слідує, що без обмеження дійсності можна прийняти
 . Дальше, для фізичного обґрунтування швидкості зручно ввести нові постійні
. Дальше, для фізичного обґрунтування швидкості зручно ввести нові постійні 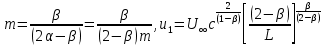 .
.При цьому формула (144) для швидкості потенціальної течії перетворюється до вигляду
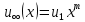 , а перетворення подібності для незалежної змінної y і функції потоку
, а перетворення подібності для незалежної змінної y і функції потоку 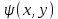 приймає вигляд [9]
приймає вигляд [9]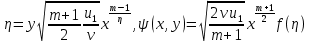 . (148)
. (148)Складові швидкості u і v визначається через
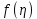 за формулою
за формулою . (149)
. (149)Функція
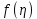 визначається як розв’язання краєвої задачі (147) з
визначається як розв’язання краєвої задачі (147) з 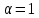 .
.Потенційна течія з
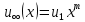 виникаєпри обтіканні клинка з кутом розчину
виникаєпри обтіканні клинка з кутом розчину 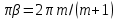 . Течія над площиною і обтікання плоских пластин відповідає частковий випадок обтікання клиноподібного тіла з
. Течія над площиною і обтікання плоских пластин відповідає частковий випадок обтікання клиноподібного тіла з 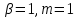 і
і 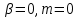 [9]. В останньому випадку для
[9]. В останньому випадку для 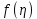 отримуємо краєву задачу
отримуємо краєву задачу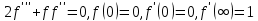 . (150)
. (150)Аналітичний розв’язок цієї задачі було отримано Г. Блазиусом за допомогою розкладу
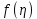 в степеневий ряд в околі точки
в степеневий ряд в околі точки 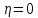 асимптотного розкладу для великих
асимптотного розкладу для великих 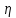 і наступного піднесення в деякий підходящий чином вибраний в точці
і наступного піднесення в деякий підходящий чином вибраний в точці 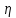 . Достатньо повні табличні значення
. Достатньо повні табличні значення 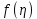 були отримані чисельним інтегруванням рівняння Блазиуса (150) за способом Рунге-Кута.
були отримані чисельним інтегруванням рівняння Блазиуса (150) за способом Рунге-Кута.У випадку
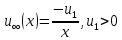 , який може бути використаний як випадок плоскої течії в звужуючому каналі з плоскими стінками (течія зі стоком), перетворення подібності
, який може бути використаний як випадок плоскої течії в звужуючому каналі з плоскими стінками (течія зі стоком), перетворення подібності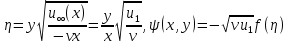 (151)
(151)Трансформує рівняння (130)в рівняння для
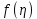 [9]:
[9]: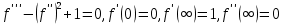 . (152)
. (152)Приєднані до цього рівняння граничні умови витікають із умов для
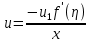 і
і  . При цій умові
. При цій умові 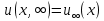 приводить до двох умов
приводить до двох умов 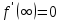 і
і 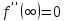 , якщо врахувати, що
, якщо врахувати, що  .
.Умова
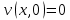 виконується автоматично.
виконується автоматично.Рівняння (151) можна отримати із рівняння (138), прийнявши
 . Розглянутий частковий випадокє одним із тих рідких випадків, коли диференціальне рівняння прикордонного шару інтегрується в замкнутій формі. Дісно, помноживши рівняння (151) на
. Розглянутий частковий випадокє одним із тих рідких випадків, коли диференціальне рівняння прикордонного шару інтегрується в замкнутій формі. Дісно, помноживши рівняння (151) на 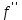 і про інтегрувавши його один раз, отримаємо
і про інтегрувавши його один раз, отримаємо 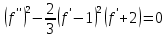 , де a є сталою інтегрування. В силу краєвих умов
, де a є сталою інтегрування. В силу краєвих умов 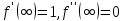 очевидно, що
очевидно, що 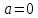 . Покладаючи
. Покладаючи 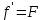 , отримуємо
, отримуємо 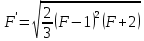 , а після інтегрування із врахуванням умови
, а після інтегрування із врахуванням умови 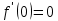 маємо
маємо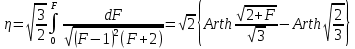 (153)
(153)Дозволивши це рівняння відносно F і враховуючи, що
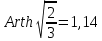 знаходимо
знаходимо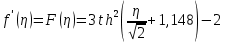 . (154)
. (154)Значення функції
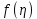 в розглянутому випадку не потрібне.
в розглянутому випадку не потрібне.Література
А.Н.Тихонов, А. А. Самарський, Рівняння математичної фізики, Держтехвидання, М., 1996.
W.P. Ames, Monlinear partial differential equations in engineering, v.1. Academic Press, New-York-London, 1965.
W.F.Ames Monlinear partial differential equations in engineering, v.11. Academic Press, New-York-London, 1972.
Г. Карслоу, Д. Егер, Теплопровідність твердих тіл, “Наука”, М. 1964.
Р. Курант, К. Фрідрікс, Надзвукові течії і ударні хвилі, М., 1961.
Л. І. Сідов, Плоскі задачі гідродинаміки і аеродинаміки. М. –Л.,1950
Л. М. Мілн-Томсон, Теоретична гідродинаміка, “Світ”, М., 1964.
G. E. Forsythe, W. R. Wasow, Finite Difference Methods for
Partial Differential Equations, Wiley, New-York, 1960.
Г. Шліхтинг, Теорія прикордонного шару, “Наука”, М., 1974.