Кам’янець-Подільський національний університет імені Івана Огієнка
Факультет фізико-математичний
Кафедра математики
Курсова робота
на тему:
«Стійкість лінійних диференціальних систем у сенсі Ляпунова ( перший метод )»
Студента 3 курсу, групи M1-B18
спеціальності:
014.04 Середня Освіта (Математика)
Величко Денис Олександровича
Керівник:
доктор фізико-математичних наук,
професор Теплінський Ю.В.
Національна шкала________
Кількість балів: __________
Оцінка :ЕCTS ____________
Члени комісії _____________ ________________
( підпис ) (прізвище та ініціали )
_____________________ __________________________
( підпис ) (прізвище та ініціали )
Вступ
Теорія стійкості руху займається дослідженням факторів, що впливають на рух матеріальної системи. Під впливовими факторами розуміються сили, що не враховуються при описі руху внаслідок їх малості в порівнянні з основними силами. Впливаючі сили зазвичай невідомі. Вони можуть діяти миттєво, що зведеться до малої зміни початкового стану матеріальної системи, тобто до початкових значень координат і швидкостей. Але ці чинники можуть діяти і безперервно, що буде означати, що складені диференціальні рівняння руху відрізняються від справжніх, що в них не враховані деякі малі поправочні члени.
Теорія стійкості руху і займається встановленням ознак, що дозволяють судити, чи буде розглянутий рух стійким або нестійким. Так як, впливові фактори завжди неминуче існують, то стає зрозумілим, що завдання стійкості руху набуває дуже важливе теоретичне і практичне значення.
Завданням стійкості руху займалися багато найвизначніших математиків і механіків. Основна теорема про стійкість рівноваги встановлена ще Лагранжем. Вона служила вихідним пунктом Для досліджень Рауса, який встановив ознаки стійкості руху для деяких окремих випадків рухів. Завданням стійкості займалися також Томсон і Тет і Н. Е. Жуковський.
Визначення стійкості руху
Найпростішими відомими прикладами стійкої і нестійкої рівноваги є, відповідно, нижня і верхня вертикальні положення маятника, коли його центр ваги не лежить на осі підвісу.
Зазначимо два основні моменти, що випливають з визначення стійкості:1) Про стійкість або нестійкість рівноваги судять за характером тих рухів, які мають місце поблизу положення рівноваги.
2) Для стійкості рівноваги необхідно, щоб відповідним вибором початкових відхилень системи від її положення рівноваги і початкових швидкостей можна було домогтися, щоб ці відхилення і швидкості залишалися менше будь-якого наперед заданого числа.
Так що, наприклад, верхнє вертикальне положення маятника, показаного на рис. 1, буде нестійким, яким би малим не був кут α, так як відхилення маятника від положення рівноваги не може бути зроблено менше α, як би не були обрані початкові умови руху.
Цілком аналогічно стійкості рівноваги визначається по Ляпунову стійкість руху.
Розглянемо довільну динамічну систему і припустимо, що її рух може бути описано системою диференціальних рівнянь, яка може бути приведена до нормального вигляду:
Тут
- деякі параметри, пов'язані з рухом, як, наприклад, координати, швидкості або взагалі деякі функції цих величин.Основні визначення по другому методу Ляпунова
Ми будемо припускати, що диференціальні рівняння обуреного руху мають вигляд:
де
не залежить явно від t.У своєму дослідженні Ляпунов припускав, що функції
представляли собою степенні ряди, розташовані за ступенями 
, що сходяться в області
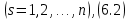
де Н - деяка постійна. Однак всі положення другого методу Ляпунова і всі пов'язані з ними докази повністю зберігають силу і при більш загальних припущеннях. Ми замінимо тому припущення Ляпунова про аналітичності функцій
значно більш загальним умовою, а саме, ми будемо тільки припускати, що функції в області (6.2) неперервні і притому такі, що рівняння (6.1) для кожної системи початкових значень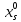 
величин , лежать в області (6.2), допускають єдине рішення.Визначення 1.
Функція
називається знако-визначною. {виразно-позитивною або виразно-негативною), якщо вона при
(6.3)де h- досить мале позитивне число, може приймати значення, тільки одного певного знака і перетворюється в нуль тільки при
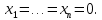
Визначення 2.
Функція
називається знако-постійною {позитивною або негативною), якщо вона в області (6.3) може приймати значення тільки одного певного знака, але може звертатися в нуль і при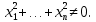 
Визначення 3.
Функція
називається знако-змінною, якщо вона не є ні знако-визначною, ні знако-постійною і, отже, яким би малим не було число h, може приймати в області (6.3) як позитивні, так і негативні значення.Пояснимо ці визначення прикладами. Припустимо для визначеності, що n = 3. Тоді функції
будуть виразно-позитивними, і при цьому величина h в нерівностях (6.3) може бути взята як завгодно великою. Функція
як ми побачимо нижче, буде також визначено-позитивною, але
тепер уже величина h повинна бути взята досить малою. Функції
будуть обидві знако-постоянні. (позитивними). Дійсно, обидві вони можуть приймати крім позитивних ще і нульові значення при значеннях
, що не рівні нулю одночасно (друга - при 
і 
довільному). Функції
будуть, очевидно, знако-змінними.
Перша теорема Ляпунова про стійкість руху.
Перша теорема Ляпунова про стійкість, яка в подальшому буде називатися теоремою А, може бути виражена таким чином:
Теорема А: Якщо для диференціальних рівнянь впливового руху можливо знайти знако-визначну функцію
повна похідна якої за часом, складена в силу цих рівнянь, є функція знако-постійного, знака, протилежної з V, або тотожне звертається в нуль, то рух стійкий.Доведення. Не порушуючи спільності міркувань, ми можемо припустити, що V є функція виразно-позитивна, так що у всіх точках області
(9,1)за винятком початку координат, V приймає тільки позитивні значення. У тій же області згідно з умовою теореми справедлива нерівність
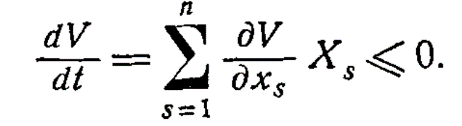
(9,2)
Нехай ε - довільне як завгодно мале позитивне число, менше h. Позначимо через х найбільшу з величин
тобто покладемо
і розглянемо множину всіх значень величин
, пов'язаних співвідношенням
(9.3)(Тобто всі точки, що лежать на гранях n-мірного куба зі стороною 2ε, ребра якого паралельні осях координат і центр якого збігається з початком координат).
Нехай l - точна нижня межа функції 
за умови (9.3), так що(9,4)
Число l буде, очевидно, позитивним, так як V може приймати на безлічі (9.1) тільки позитивні значення, і при цьому в силу безперервності V нижня межа цієї функції на безлічі (9.3) є одне зі значень, які вона на цій множині приймає.
Розглянемо тепер довільне рішення
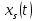диференціальних рівнянь руху, початкові значення 
якого лежать в області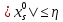
(9.5)Ми будемо при цьому припускати, що число
менше, ніж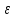 
, і що воно настільки мале, що
Такий вибір числа
, очевидно можливий , так як V - функція безперервна і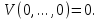 
Підставляючи рішення
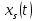в функцію V, ми отримаємо функцію від часу, яка в силу (9.2) буде не зростаючою, принаймні до тих пір, поки величини 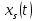будуть залишатися в області (9.1). Отже, при всіх t, при яких 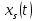лежать в області (9.1), буде виконуватися нерівність
Звідси безпосередньо випливає, що при всіх t >
будуть виконуватися нерівності
(9,7)Справді, так як
, то нерівності (9.7) будуть виконуватися в силу безперервності 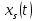, хоча б при значеннях t, досить близьких до . І якщо тому ці нерівності коли-небудь взагалі порушуються, то повинен існувати такий момент часу t = T, при якому хоча б одна з величин чисельно досягне значення ε. Іншими словами, повинен існувати такий момент часу t = T, при якому буде виконуватися умова (9.3), і, отже, на підставі (9.4)
Це, однак, неможливо, так як в силу ε < h множина (9.3) лежить в області (9.1) і, отже, при x = ε має виконуватися нерівність (9.6).
Таким чином, для всіх рішень диференціальних рівнянь руху, для яких виконуються нерівності (9.5), будуть при всіх t >
виконуватися нерівності (9.7), що і доводить стійкість руху.Друга теорема Ляпунова про стійкість руху.
Теорема Б. Якщо для диференціальних рівнянь руху можливо знайти знако-визначну функцію
, повна похідна якої за часом, складена в силу цих рівнянь, є функція також знако-визначною, знако-протилежною з V, то рух є стійким асимптотично.Доведення. Не порушуючи спільності міркувань, ми можемо, так само як і раніше, припустити, що V є функція виразно-позитивна і, отже
- виразно-негативна, так що в області (9.1) виконуються умови
причому знаки рівності можливі тільки при
.Нехай ε довільне позитивне число, менше h. Так як в даному випадку виконуються умови попередньої теореми, то рух у всякому разі стійкий.
Тому знайдеться таке позитивне число
, що для будь-якого рішення 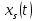рівнянь (6.1), для якого в початковий момент часу t = виконуються нерівності
(10,1)будуть при всіх t >
виконуватися нерівності
Покажемо, що при цьому будемо мати:
(10,2)т. е. що рух стійко асимптотичний. Справді, так як розглядаєме рішення весь час лежить в області (9.1), то похідна за часом функції
буде за умовою теореми залишатися весь час негативною, не перетворюючись в нуль ні при яких значеннях t. Останнє випливає з тієї обставини, що функції
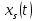не можуть перетворитись в нуль одночасно ні при яких значеннях t, бо якби це мало місце при якомусь значенні t = T, то, прийнявши Т за початковий момент часу, ми мали б два різних рішення рівнянь (6.1) з нульовими початковими значеннями: розглядаєме 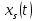і тривіальне 
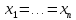. Це, однак, неможливо, так як рівняння (6.1) є такими, що для них при заданих початкових умовах існує тільки одне рішення.Отже, похідна
залишається весь час негативною. Отже, функція буде монотонно спадною і тому вона при 
буде необхідно прагнути до деякої межі α, залишаючись весь час більше цієї межі, так що весь час матимемо:
(10.3)Доведемо, що α = 0. З цією метою допустимо супротивне: α
і, отже, в силу позитивності V, α > 0. Так як V є функція неперервна, то з (10.3) випливає, що
(10.4)де а - деяке позитивне число. Але так як є функція виразно-негативна, то з (10.4) випливає, що
де b - також позитивне число.
Отже, при всіх t >
буде виконуватися нерівність
що, очевидно, неможливо, так як права частина цієї нерівності при досить великих t робиться негативною, що суперечить умові позитивності
Таким чином, ми приходимо до висновку, що
звідки внаслідок знако-визначеності V випливає (10.2), що і доводить теорему.
Теореми Ляпунова про стійкість для змінних рухів.
Розглянемо диференціальні рівняння руху виду:(46.1)
де функції визначені в області(46.2)
Ми будемо припускати, що в зазначеній галузі функції
є безперервними і задовольняють деяким загальним умовам, які забезпечують існування для рівнянь (46.1) єдиного рішення, що задовольняє заданим початковим умовам.Перша основна теорема Ляпунова, яку ми надалі будемо називати теоремою I, може бути сформульована таким чином.
Теорема I: Якщо для диференціальних рівнянь руху (46.1) можна знайти знако-визначну функцію
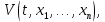для якої похідна по часу, складена в силу цих рівнянь, тобто вираз
(46.3)
є функція знакопостійна, знакопротилежна з V, або тотожно перетворюється в нуль, то рух стійкий.
Доведення: Припустимо для визначеності, що V - функція позитивна. Отже, існує таке досить велике число
і таке досить мале число h 
Н, що в області 
(46.4)виконується нерівність
(
46.5)де W – деяка, що не залежить від t визначно-позитивна функція. Крім того, в цій же області вираз (46.3) може приймати тільки негативні або рівні нулю значення.
Нехай ε - довільне як завгодно мале позитивне число. Ми будемо припускати, що у всякому разі ε < h. Розглянемо сукупність всіляких значень величин
, пов'язаних співвідношенням(
46.6)і позначимо через l точну нижню межу функції W за цієї умови. В силу знаковизнаночності W число l позитивно і відмінно від нуля. В силу (46.5) маємо:
(46.7)Будемо тепер розглядати величини
як функції часу, що задовольняють диференціальним рівнянням руху. Припустимо, що початкові значення 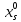цих функцій при t = обрані згідно нерівностям 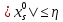, (46,8)Де
настільке мале, що(
49.9)В силу того, що
, такий вибір числа , очевидно, можливий. Ми будемо припускати, що число у всякому разі менше ε. Тоді нерівності , (46.10)виконуючись в початковий момент часу, будуть виконуватися, по крайній мірі, при t -
досить малому, так як функції (t) змінюються з плином часу безперервно. Покажемо, що ці нерівності будуть виконуватися при всіх t > . Справді, якби ці нерівності коли-небудь порушилися, то мав би існувати такий момент часу t = Т, для якого хоча б одне з цих нерівностей перейшло б в рівність. Іншими словами, ми мали б
і, отже, на підставі (46.7)
(46.11)З іншого боку, так як ε < h, то у всьому інтервалі часу
виконуються нерівності (46.4), а отже, у всьому цьому інтервалі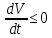 
. Це дає:
що на підставі (46.9) суперечить (46.11). Таким чином, нерівності (46.10) повинні виконуватися при всіх t >
, звідки і випливає стійкість руху.Теорема II. Якщо при виконанні умов теореми I похідна є знаковизначною, а сама функція V допускає нескінченно малу найвищу межу, то рух стійко асимптотичний.
Доведення. Припустимо, що V є функція виразно-позитивна і, отже, виразно-негативна. Таким чином, в області (46.4) буде виконуватися не тільки нерівність (46.5), але і нерівність
(46.12)
де
- яка не залежить від t виразно-позитивної функції.Будемо розглядати величини
як функції часу, що задовольняють диференціальним рівнянням обуреного руху, припускаючи, що початкові значення 
цих величин задовольняють нерівності (46.8). Так як рух у всякому разі стійкий, то величину можна вибрати настільки малою, щоб при всіх t > величини залишалися в області (46.4). Тоді на підставі (46.12) похідна від функції 
буде весь час негативною і, отже, ця функція з необмеженим зростанням t буде прагнути до деякого межі, залишаючись весь час більше цієї межі. Покажемо, що ця межа дорівнює нулю. Припустимо супротивне, що ця межа дорівнює деякій позитивній величині α, відмінною від нуля. Тоді при всіх t > буде виконуватися нерівність 
(46.13)Так як V допускає нескінченно малу найвищу межу, то з цієї нерівності випливає, що
(46.14)де λ - деякий досить мале позитивне число. Дійсно, якби такого числа λ не існувало, тобто, якби величина
була менше будь-якого як завгодно малого числа, то і величина 
, як це випливає з визначення нескінченно малого вищого краю, була б також як завгодно малою, що суперечить (46.13).Але якщо при всіх t >
виконується нерівність (46.14), то (46.12) показує, що весь час буде також виконуватися нерівність
де l - відмінне від нуля позитивне число, яке є точною нижньою межею функції
за умови (46.14).О
тже, при всіх t > матимемо:
що, очевидно, знаходиться в протиріччі з (46.13). Отримане протиріччя показує, що функція
з необмеженим зростанням t прямує до нуля. Отже, те ж саме буде і для функції 
звідки безпосередньо випливає
що й доводить теорему.
Теорема Ляпунова про нестійкість для змінних рухів.
Теорема III. Якщо існує припускаюча нескінченно мала вища межа функції
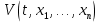, похідна якої за часом, складена в силу рівнянь руху, є функція знаковизначна, а сама функція V при значеннях , як завгодно малих, і при значеннях t, як завгодно великих, може приймати значення того ж знака, що і похідна, то рух неcтійкий.Доведення. Приймемо для визначеності, що похідна
позитивна. Отже, в області
(47.1)
виконується нерівність(47.2)
де
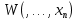- не залежить від t виразно-позитивна функція.Нехай
- довільне як завгодно мале позитивне число. Розглянемо рішення 
рівнянь руху, для якого початкові значення обрані відповідно до умов
Згідно з умовами теореми такий вибір величин
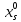можливий, яким би малим не було число . Покажемо, що рішення яке роздивляється обов'язково вийде в певний момент часу з області (47.1).Справді, припустимо, що це рішення весь час залишається в області (47.1). Тоді на підставі (47.2) похідна від функції
буде в усякому разі позитивної, і ми, отже, маємо:
(47.3)
Так як V допускає нескінченно малу найвищу межу, то з (47.3) слідує:(47.4)
де λ - досить мале позитивне число. Але тоді з (47.2) випливає, що(47.5)
де відмінне від нуля позитивне число l є точною нижньою межею функції
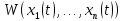за умови (47.4).Нерівність (47.5) дає:
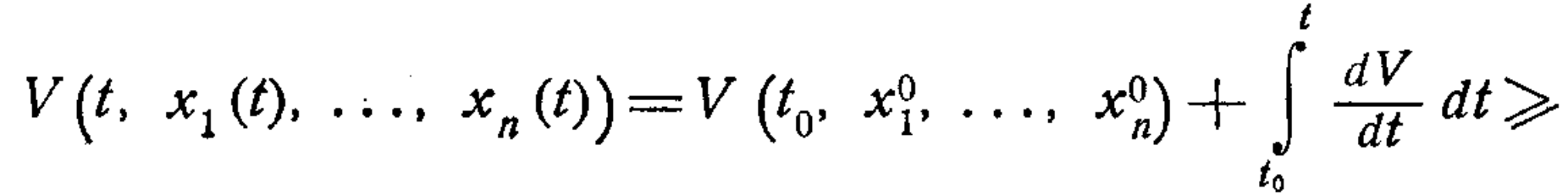
що неможливо, так як функція V, допускаючи нескінченно малу вищу межу, буде в усякому разі обмеженою.
З отриманого протиріччя випливає, що рішення
в певний момент часу обов'язково покине незалежну від початкових значень 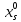область (47.1), і так як ці початкові значення як завгодно малі, то рух нестійкий. Таким чином, теорема доведена.Висновок
Я ознайомився з Теорією Стійкості Руху та її впливом на матеріальні системи. Дізнався хто попередньо працював над цією теорією та виніс основні твердження про неї. Мав досвід розкрити для себе головні тезиси першого методу Ляпунова для стійкості руху та працювати з його основними теоремами.
Джерела
Б.П. Демидович. Лекции по математической теории устойчивости – М., 1967 р. - 472 с. з ілюстраціями.