1   2   3
Ім'я файлу: Algebra-ispit (1).docx
Розширення: docx
Розмір: 1325кб.
Дата: 27.04.2021
скачати
Пов'язані файли:
Класи вантажу.docx
Petrushenko_business.pdf





  1. Степенева функція, її властивості та графіки.

Степеневою наз. функція, яка задається формулою у = хn, де n –число, х – незалежна змінна.

Властивості функції у = хn, де n ∈ N

  1. Область визначення – множина R всіх дійсних чисел.

  2. Область значень: якщо n – парне, то [0; + ∞), якщо n – непарне, то (-∞; + ∞).

  3. Якщо n – парне, то функція парна, тобто у(-х) = у(х), її графік симетричний відносно початку координат.

  4. Точки перетину з осями графіка функції: при х=0, у=0, (0; 0). Графік проходить через початок координат.

  5. Монотонність: якщо n – парне, то функція спадає при х ∈ (-∞; 0], функція зростає при х ∈[0; +∞); якщо n – непарне, то функція зростає на всій області визначення.

  6. Знакосталість: якщо n – парне, то у>0 при х≠0; якщо n – непарне, то у>0 при х>0, у<0 при х<0.



Парна непарна
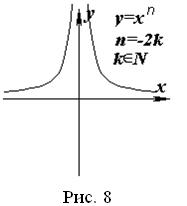
Властивості функції у = х–n, де n ∈ N

  1. Область визначення – множина R всіх дійсних чисел, крім 0, тобто х ∈ (-∞; 0)∪(0; +∞).

  2. Область значень: якщо n – парне, то (0; + ∞), якщо n – непарне, то (-∞; 0)∪(0; + ∞).

  3. Якщо n – парне, то функція парна, тобто у(-х) = у(х), її графік симетричний відносно осі Оу; якщо n – непарне, то функція непарна, тобто у(-х) = –у(х), її графік симетричний відносно початку координат.

  4. Точок перетину з осями координат графік немає.

  5. Монотонність: якщо n – парне, то функція зростає при х ∈ (-∞; 0), функція спадає при х ∈(0; +∞); якщо n – непарне, то функція спадає на всій області визначення, тобто при х ∈ (-∞; 0) і х∈(0; + ∞).

  6. Знакосталість: якщо n – парне, то у>0 при х≠0, тобто при х ∈ (-∞; 0) і х∈(0; + ∞); якщо n – непарне, то у>0 при х ∈ (0; +∞), у<0 при х ∈ (-∞; 0).

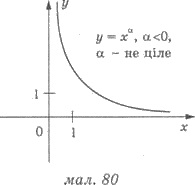
Властивості функції у = ха, де а – неціле число

1) Область визначення: якщо а >0, то х ∈ [0; +∞), якщо а<0, то х ∈ (0; +∞).

  1. Область значень: якщо а >0, то у ∈ [0; +∞), якщо а<0, то у ∈ (0; +∞).

  2. Функція ні парна, ні непарна.

  3. Якщо а>0, то графік функції проходить через початок координат; якщо а<0, то графік функції точок перетину з осями координат немає.

  4. Монотонність: якщо а>0, то функція зростає на всій області визначення, тобто при х ∈ [0; +∞); якщо а<0, то функція спадає на всій області визначення, тобто при х∈(0; + ∞).

  5. Знакосталість: у>0 при х ∈ (0; +∞).


Властивості функції у = 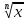, де n ≥2, n∈ N

  1. Область визначення: якщо n – парне, то х ∈ [0; + ∞), якщо n – непарне, то х ∈ (-∞; + ∞).

  2. Область значень: якщо n – парне, то у ∈ [0; + ∞), якщо n – непарне, то у ∈ (-∞; + ∞).

  3. Якщо n – парне, то функція ні парна, ні непарна; якщо n – непарне, то функція непарна, тобто у(-х) = –у(х), її графік симетричний відносно початку координат.

  4. Якщо х=0, то у=0, тобто графік проходить через початок координат.

  5. Монотонність: функція зростає на всій області визначення.

  6. Знакосталість: якщо n – парне, то у>0 при х ∈ (0; + ∞); якщо n – непарне, то у>0 при х ∈ (0; +∞), у<0 при х ∈ (-∞; 0).



Ні парна, ні непарна Непарна

  1. Ірраціональні рівняння та їх системи: поняття та способи розв’язання

Рівняння називають ірраціональним, якщо воно містить невідомі під знаком кореня.

Система рівнянь називається системою ірраціональних рівнянь, якщо серед рівнянь системи є ірраціональні рівняння.

Розв’язування ірраціональних рівнянь здійснюється заміною ірраціонального рівняння на рівносильне йому раціональне рівняння, або раціональне рівняння, яке є його наслідком.

Починати розв’язування ірраціонального рівняння слід з визначення області допустимих значень рівняння, оскільки рівняння може бути невизначеним на множині дійсних чисел і дійсних розв’язків не мати.

Основними методами розв’язування ірраціональних рівнянь є через ОДЗ, піднесення обох частин рівняння до одного і того самого степеня; заміна змінної; графічний і т.д.

При переході від рівняння f(x) = g(x) до рівняння (f(x))2n = (g(x))2n можуть з’явитися сторонні корені, тому після розв’язування рівняння треба зробити перевірку знайдених коренів безпосередньою підстановкою кожного кореня у вихідне рівняння. Якщо при цьому дістаємо неправильну рівність, то корінь, що перевіряється, є стороннім коренем і не є коренем заданого рівняння; якщо дістаємо правильну рівність, то такий корінь є коренем заданого рівняння.

Методи розв’язання

1. Піднесення обох частин рівняння до одного і того ж степеня. Одержане рівняння є наслідком вихідного рівняння.

Зауваження. Якщо однократним піднесенням до степеня ірраціональність не була виключена, одержане рівняння можна спростити і повторити піднесення до степеня обох частин рівняння

2. Введенням нової змінної задане рівняння зводиться до квадратного.

3. Рівняння, одна з частин якого є сумою або різницею квадратних коренів із виразів, які відрізняються на число, а друга частина є числом, розв’язується домноженням обох частин рівняння на спряжений вираз і наступним розв’язуванням системи рівнянь заданого й одержаного.

Розв’язування ірраціональних рівнянь ґрунтується на приведенні їх за допомогою деяких перетворень до раціонального рівняння. Як правило, це досягається піднесенням обох частин ірраціонального рівняння до одного і того самого степеня (інколи кілька разів).

При піднесенні обох частин рівняння до парного степеня одержане рівняння може мати корені, що не задовольняють даному рівнянню. Такі корені називаються сторонніми для даного рівняння. (Це відбувається тому, що з рівності парних степенів двох чисел не випливає рівність цих чисел.)

Тому слід обов’язково робити перевірку одержаних коренів.

Розв’язування систем ірраціональних рівнянь передбачає звільнення від ірраціональності за допомогою методів, які застосовуються в розв’язанні ірраціональних рівнянь.

  1. Ірраціональні нерівності: поняття та способи їх розв’язання

Ірраціональною називається нерівність, у якій змінна знаходиться під знаком кореня.

Розв’язування ірраціональних нерівностей здійснюється зведенням ірраціональних нерівностей до рівносильних їм систем раціональних нерівностей або сукупності таких систем.

Універсальний метод розв’язання ірраціональних нерівностей f1(x) ≶ f2(x)

  1. Скласти функцію F(x)=f1(x)–f2(x)

  2. Знайти ОДЗ функції F(x).

  3. Знайти всі корені функції F(x), тобто розв’язати рівняння F(x) = 0 (сторонні корені відкинути).

  4. За допомогою коренів розбити ОДЗ функції F(x) на проміжки знакопостійності.

  5. Визначити знаки функції F(x) на кожному з проміжків, тобто знайти множину значень аргумента x, при яких функція F(x) приймає додатні значення, для F(x) > 0 або F (x) ≥ 0. Аналогічно розв’язують нерівності F(x) < 0 або F(x) ≤ 0.

  6. Записати відповідь



  1. Показникова функція, її властивості і графік.

Показниковою називається функція виду ах, де а>0, а≠1.

Властивості показникової функції:

1. Область визначення: х∈(-∞; +∞).

2. Область значень: у∈(0; +∞).

3. Функція ні парна, ні непарна.

4. Точки перетину з осями координат: з віссю ординат (0;1) ; з віссю абсцис точок перетину немає.

5. Проміжки зростання і спадання:

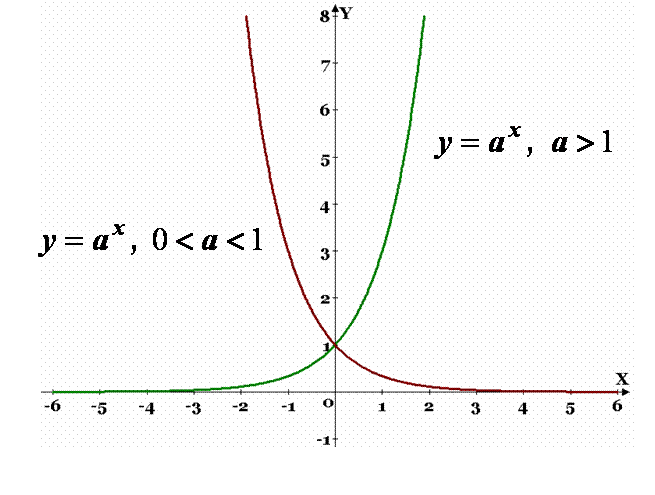
Функція у=ах при а>1  зростає на всій області визначення.

функція у=ах  при 0<а<1  спадає на всій області визначення.

6. Проміжки знакосталості: у>0 при всіх значеннях аргументу.

7. Найбільшого і найменшого значень функція не має.



  1. Показникові рівняння та їх системи: поняття та методи їх розв'язання

 Показниковими  називають рівняння, у яких змінна входить у показник степеня (а основа цього степеня не містять змінної).

Розв’язання показникових рівнянь ґрунтується на такій властивості степенів:

а 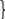х = ау

а >0, а≠1 ↔ х=у

Найпростішим показниковим рівнянням називають рівняння ах = b (a>0), а його розв’язок залежить від чисел a і b:

  1. а >0, а≠1, b>0 → x=logab,

  2. а >0, b<0 → x ∈0 ,

  3. 1 x=b≠1 → x ∈0 ,

  4. 1x=1 → x ∈ (-∞; +∞)

Основне показникове рівняння – це рівняння аf(x) = аg(x) (а>0),  а його розв’язання  залежить від числа a:

  1. при а >0, а≠1 аf(x) = аg(x) ↔ f(x) = g(x).

  2. при а =1 1f(x) = 1g(x) ↔ х∈ D(f) ∩D(g).

Найпростіше показникове рівняння – окремий випадок (g(x)=const) основного показникового рівняння, до якого на основі означення логарифма зводиться і рівняння

аf(x) = bg(x) (a, b >0, a≠b, a≠1, b≠1)

аf(x) = bg(x) ↔ аf(x) =

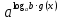
Способи розв’язування показникових рівнянь:

  1. спосіб приведення рівняння до спільної основи аf(x) = аg(x);

  2. спосіб винесення спільного множника за дужки;

  3. спосіб приведення рівняння або нерівності до квадратного;

  4. графічний спосіб;



  1. Показникові нерівності: поняття та методи їх розв'язання



  1. Логарифмічна функція, її властивості та графік

Логарифмічною наз. функція, яка задається формулою виду у =  logax, де а – число,

а>0, а ≠ 1, х – незалежна змінна.

Властивості логарифмічної функції:

  1. Область визначення – множина додатних чисел, тобто D(у) = (0; +∞).

  2. Область значень – множина R усіх дійсних чисел, тобто Е(у) = (-∞; +∞).

  3. Функція ні парна, ні непарна.

  4. Точки перетину графіка функції з осями координат:

з Ох: у=0, logax=0, х=а0, тобто х=1; (1; 0)

з Оу: точок перетину немає.

  1. Монотонність: при а>1 функція зростає на всій області визначення; при 0<а<1 функція спадає на всій області визначення.

  2. Знакосталість: якщо а>1, то у>0 при х>0 і у<0 при 0<х<1; якщо 0<а<1, то у>0 при 0<х<1 і у<0 при х>1.



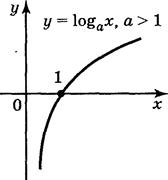
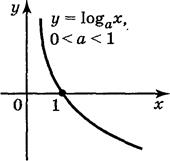
  1. Логарифмічні рівняння та їх системи: поняття та методи їх розв'язання

Логарифмічними рівняннями називають рівняння, які містять змінну під знаком логарифма.

Розв'язати логарифмічне рівняння – це означає знайти всі його корені або довести, що рівняння коренів не має.

Найпростіше логарифмічне рівняння має вигляд log х = b, де а > 0, а ≠ 1, х > 0. За означенням логарифма випливає, що х = аb.

Інший вигляд найпростішого логарифмічного рівняння такий:

loga x = logab, де а > 0, а ≠ 1, х > 0, b > 0.

Із цього рівняння випливає, що х = b. Дійсно із рівності logax = loga b на підставі означення логарифма і основної лога­рифмічної тотожності маємо:

x = 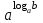= b.

Найпростішим логарифмічним рівнянням є рівняння logx a = b, де х > 0, х ≠ 1, а > 0.

За означенням логарифма маємо: хb = а, звідси х = .

Основні методи розв’язування логарифмічних рівнянь

1. Метод зведення логарифмічного рівняння до алгебраїчного.

2. Метод потенціювання.

3. Метод зведення логарифмів до однієї основи.

4. Метод логарифмування.

5. Графічний метод розв’язування логарифмічних рівнянь.

При розв’язуванні систем логарифмічних рівнянь використовують такі самі способи, що й при розв’язуванні алгебраїчних систем.

  1. Логарифмічні нерівності: поняття та способи їх розв'язання

Як відомо, логарифмічна функція у = logа х зростає при a > 1,спадає — при 0 < a < 1. Із зростанням функції у = logаx у першому випадку і спадання — у другому випадку випливає:

1) При a > 1 нерівність logа х2 > logа х1 рівносильна системі

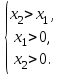
2) При 0 < a < 1 нерівність logа х2 > logа х1 рівносильна системі
Розв’язуючи логарифмічні нерівності, спираються на такі твердження.
1. Якщо а>1, то нерівність   рівносильна подвійній нерівності  .
Це твердження можна записати у вигляді:

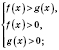
або 
2. Якщо  , то нерівність   рівносильна подвійній нерівності  .
Це твердження можна записати у вигляді:

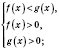
або 
Зверніть увагу: при розв’язуванні логарифмічної нерівності немає сенсу окремо виписувати ОДЗ, оскільки все одно буде необхідно розв’язувати систему нерівностей, яка включає й ОДЗ.

15. Обернені тригонометричні функції

Функція у = sin х зростає на проміжку 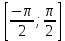  і приймає всі значення від -1 до 1, тобто кожне своє значення функція приймає в єдиній точці області визначення. Отже, рівняння sin х = а, │а│≤ 1 на проміжку  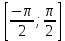 має єдиний корінь, який називається арксинусом числа а і позначається arcsin a.

Арксинусом числа а називається таке число із проміжку 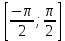 синус якого дорівнює а.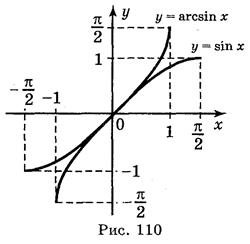



 Влас­тивості функції у = arcsin х.
1. D(y) = [-1; 1].

2. Е(у) =  .

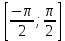3. Графік симетричний відносно початку координат (функція непарна) arcsin (-х) = -arcsin х.

4. Функція зростаюча. Якщо х1 > х2 то arcsin х1 > arcsin х2

5. у = 0, якщо х = 0.

6. уmах = y(1) = 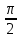  , ymіn = y(-1) = - .
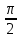Функція у = cos x спадає на відрізку [0; π] і приймає всі значення від -1 до 1, тому рівняння cos x = а, |а| < 1 на проміжку [0; π] має єдиний корінь, який називається арккосинусом числа а і позначається arccos a.

Арккосинусом числа а називається таке число з проміжку [0; π], косинус якого дорівнює а.



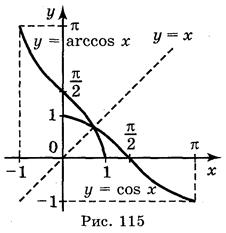
Розглянемо властивості функції у = arccos х.

1. D(y) = [-1; 1].

2. Е(y) = [0;π].

3. Графік не симетричний ні віднос­но початку координат, ні віднос­но осі OY. arccos (-х) = π - arccos х.

4. Функція спадна. Якщо х1 > х2 то arccos х1 < arccos х2.

5. у = 0, якщо х = 1.

6. уmах = y(-1) = π, ymіn = y(1) = 0.

16. Тригонометричні рівняння та їх системи: поняття та способи розв'язування

Тригонометричним рівнянням називається рівність, яка містить змінну тільки під знаком тригонометричних функцій і правильна при деяких певних конкретних значеннях зміни. Ці значення наз. коренями (розв’язками) рівняння.

Найпростіші тригонометричні рівняння:

sin x = a, якщо 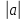>1, то рівняння дійсних коренів немає, якщо 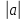≤1, то х = 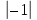k

arcsin a + πk, k∈Z.

Окремі випадки: 1) sin x = 0, тоді х= πk, k∈Z.

2) sin x = –1, тоді х =

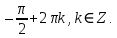
3) sin x = 1, тоді х =

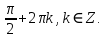
cos x = a, якщо 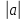>1, то рівняння дійсних коренів немає,

якщо 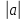≤1, то x = ± arccos a + 2πk, k∈Z.

Окремі випадки: 1) cos x = 0, тоді х=

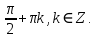
2) cos x = –1, тоді х =

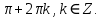
3) cos x = 1, тоді х =

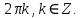
tg x = a, x = arctg a + πk, k∈Z,

ctg x = a, x = arcctg a + πk, k∈Z.

Способи розв'язання:

1. Якщо тригонометричне рівняння містить лише одну тригонометричну функцію з одним і тим самим аргументом, то позначивши цю функцію новою змінною, отримаємо алгебраїчне рівняння відносно цієї змінної.

2. Часто після використання відповідних тригонометричних формул вдається звести рівняння до однієї функції одного й того самого аргументу, після чого застосувати заміну змінних.

3. Метод розкладання на множники.

Розв'язуючи системи триногометричних рівнянь, використовуємо ті самі прийоми, що і при розв'язуванні систем алгебраїчних рівнянь, а також формули тригонометрії. Розв'язуючи системи триногометричних рівнянь їх зводять або до одного рівняння з одним невідомим, або до системи рівнянь відносно самих аргументів чи функцій цих аргументів.

17. Тригонометричні нерівності: поняття та способи розв'язування

Нерівності, що містять невідомі під знаками тригонометричних функцій, називають тригонометричними нерівностями.

Найпростіші тригонометричні нерівності:

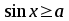або ;

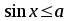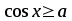або , ;

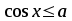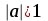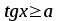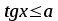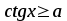або ;

або ,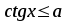

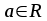
мають такі множини розв’язків:

Вид нерівності
Множина розв’язків нерівності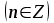

































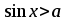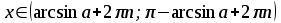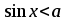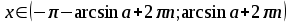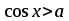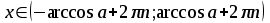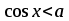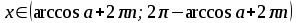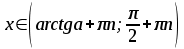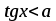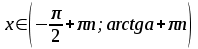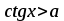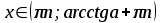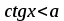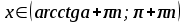Для розв’язування складніших тригонометричних нерівностей треба здійснювати перехід до однієї або декількох найпростіших нерівностей, які розв’язуються за допомогою одиничного кола або графіків тригонометричних функцій.

18. Співвідношення між тригонометричними функціями одного аргументу.



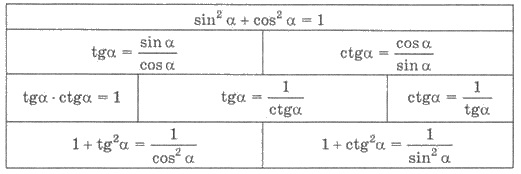
19. Формули перетворення добутку тригонометричних функцій у суму.



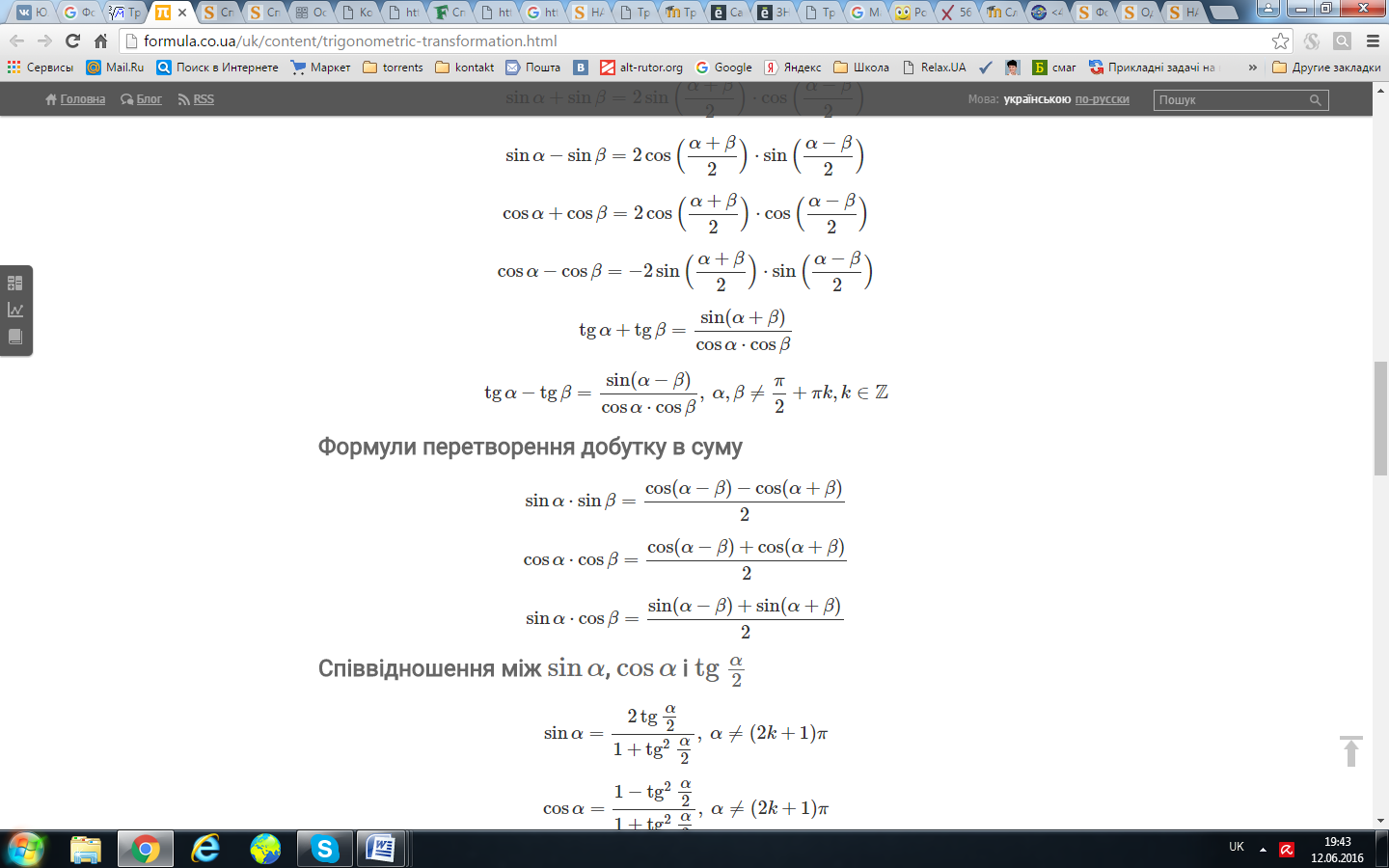
20. Формули додавання аргументів тригонометричних функцій.













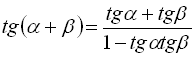
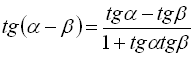
21. Формули подвійного та половинного аргументу тригонометричних функцій.

Формули подвійного аргументу



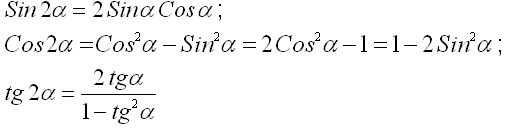
Формули половинного аргументу



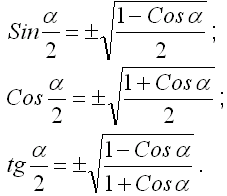
22. Первісна та її властивості.

Функцію F(х) називають первісною для функції f(x) на заданому проміжку, якщо для всіх х з цього проміжку F'(х) = f(х).
Основна властивість первісної

Якщо функція F(x) є первісною для функції  f(x) на даному проміжку, а  C  – довільна стала, то  F(x)+C  є також первісною для функції  f(x), при цьому будь-яка первісна для функції  f(x) на даному проміжку може бути записана у вигляді F(x)+C , де С – довільна стала.



 

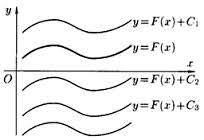
Графіки будь-яких первісних одержуються один з одного паралельним перенесенням уздовж осі ОУ.

23. Криволінійна трапеція і її площа. Обчислення площ і об'ємів з допомогою визначеного інтеграла.

Нехай на відрізку [а; b] осі абсцис задано неперервну функцію у = f(x), яка на цьому відрізку набуває лише тільки невід’ємні значення. Фігуру, обмежену графіком функції у = =f(х), віссю абсцис та прямими х = а, х = b називають криволінійною трапецією. Її площу S можна знайти за формулою:

S =

2)

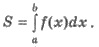
3) S = –

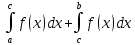
4) S =
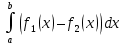
Об'єм:

1)

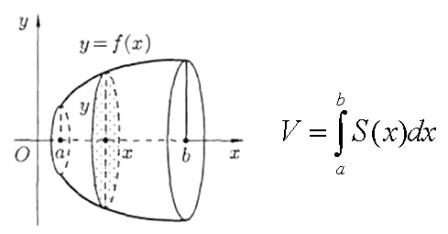
2)

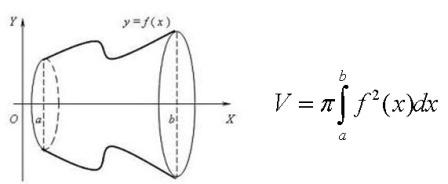
24. Границя функції. Неперервність функції.

Число А називають границею функції 𝑓(𝑥) при 𝑥 → ∞ і пишуть 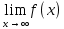= 𝐴, якщо для довільного числа 𝜀 > 0 існує таке число 𝑀 = 𝑀(𝜀) > 0, що при 𝑥 > 𝑀 виконується нерівність 𝑓 𝑥 − 𝐴 < 𝜀.

Функція у=f(x)  називається неперервною в точці x0, якщо границя функції в точці x0 дорівнює значенню функції в цій точці:



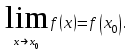
Властивості неперервних функцій.

Теорема 1. Сума скінченного числа функцій, неперервних у точці а, є функція, неперервна в цій точці.

Теорема 2. Добуток скінченного числа функцій, неперервних у точці а, є функція, неперервна в цій точці.

Теорема 3. Відношення двох функцій, неперервних у точці а, є функція, неперервна в цій точці, якщо значення функції у знаменнику відмінне від нуля в точці а.

Теореми 1, 2, 3 випливають із відповідних теорем для границь функцій.

Теорема 4. Многочлен є функція, неперервна на всій числовій прямій.

Теорема 5. Будь-яка дробово-раціональна функція неперервна в кожній точці своєї області визначення.

Теорема 6. Якщо функція f неперервна на відрізку [a; b] і на кінцях його набуває значень різних знаків, то всередині відрізка [a; b] знайдеться хоча б одна точка, в якій ця функція обертається в нуль.

Теорема 7. Якщо функція неперервна на відрізку, то серед значень, які вона набуває на цьому відрізку, існують найменше і найбільше значення. При цьому вона набуває всі значення між найбільшим і найменшим значенням.

35. Означення та ознаки перпендикулярних прямих у просторі.

Дві прямі називаються перпендикулярними, якщо вони перетинаються під прямим кутом.

Теорема 1. Якщо дві прямі, які перетинаються, відповідно паралельні двом перпендикулярним прямим, то вони теж перпендикулярні. 

Теорема 2. Через будь-яку точку прямої у просторі можна провести безліч перпендикулярних до неї прямих.

Ознака перпендикулярності прямої і площини: пряма, яка перетинає площину наз. перпендикулярною до цієї площини, якщо вона перпендикулярна до будь-якої прямої, що лежить в цій площині і проходить через точку перетину.

Теорема (ознака перпендикулярності прямої і площини). Якщо пряма перпенди­кулярна до двох прямих, які лежать у площині й перетинаються, то вона перпендикулярна до даної площини.

Властивості прямої і площини перпендикулярних між собою:

1. Теорема. Якщо площина перпендикулярна одній з двох паралельних прямих, то вона перпендикулярна й інший.

 2. Теорема. Дві прямі, перпендикулярні одній і тій же площині, паралельні.

36. Означення та ознаки прямої, перпендикулярної до площини в просторі.

Дві прямі називають перпендикулярними, якщо кут між ними дорівнює 90°.

Пряма називається перпендикулярною до площини, якщо вона перетинає цю площину і перпендикулярна до будь-якої прямої, що лежить у площині і проходить через точку перетину.

Теорема (ознака перпендикулярності прямої і площини). Якщо пряма, яка перетинає площину, перпендикулярна до двох прямих цієї площини, що проходить через точку перетину, то вона перпендикулярна до площини.

Властивості прямої і площини перпендикулярних між собою:

1. Теорема. Якщо площина перпендикулярна одній з двох паралельних прямих, то вона перпендикулярна й інший.

 2. Теорема. Дві прямі, перпендикулярні одній і тій же площині, паралельні.

38. Паралельне проектування та його властивості.

Для зображення просторових фігур на площині часто використовують паралельне проектування.

Властивості паралельного проектування:

  1. Прямолінійні відрізки фігури зображуються на площині рисунка відрізками або точками. (Якщо відрізок, що проектується, паралельний напрямку проектування, він проектується в точку.)

  2. Паралельні відрізки фігури зображуються на площині рисунка паралельними відрізками.

  3. Відношення відрізків однієї прямої або паралельних прямих зберігається при паралельному проектуванні.

При паралельному проектуванні не зберігаються ані довжина відрізка, ані величина кута.

Із властивостей паралельного проектування випливають такі твердження.

  1. Будь-який трикутник може бути зображений довільним трикутником.

  2. Якщо UABC проектується у UA1B1C1, то медіани проектуються в медіани, середні лінії – у середні лінії, а висоти й бісектриси не проектуються у висоти й бісектриси. Проте основа проекції бісектриси поділяє сторону проекції трикутника у тому ж відношенні, що основа бісектриси поділяє сторону трикутника.

3. Паралелограм зображується паралелограмом. Прямокутник, квадрат, ромб – паралелограмом загального виду.

4. Трапеція зображується трапецією. Рівно­біч­ність або прямокутність не зберіга­ється.

5. Коло зображується еліпсом.

39. Двогранний кут: поняття та способи побудови

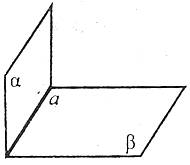Двогранним кутом називається фігура, утворена двома півплощинами із спільною прямою, що їх обмежує. Півплощини називаються гранями, а пряма, що їх обмежує – ребром двогранного кута.

Лінійним кутом двогранного кута називається кут, утворений в результаті перетину двогранного кута з площиною, яка перпендикулярна до ребра двогранного кута.

Мірою двогранного кута називається міра відповідного йому лінійного кута.

Способи побудови лінійного кута двогранного кута:

  1. На ребрі кута позначаємо точку; через неї в гранях кута проводимо дві півпрямі, перпендикулярні до ребра кута. Кут, утворений цими півпрямими, – лінійний кут поданого двогранного кута;

  2. На одній із граней кута позначаємо точку і через неї проводимо перпендикуляри до площини іншої грані та до ребра кута. Тоді одержаний кут (або суміжний з ним) є лінійним кутом двогранного кута. Цей спосіб неприйнятний у випадку, якщо двогранний кут прямий.



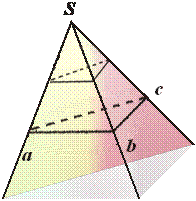
4 0. Тригранний та многогранний кут.

Тригранним кутом (аbс) називається фігура, яка складається з трьох плоских кутів (ab), (bс), (ас),

Ці плоскі кути називаються гранями тригранного кута, а їх сторони а, b, с – ребрамитригранного кута. Спільна вершина плоских кутів (точка S) називається вершиною тригранного кута. Двогранні кути, утво­рені гранями тригранного кута, називаються двогранними кутами три­гранного кута.

Теорема 1. У тригранному куті кожний плоский кут менший за суму двох інших.

Теорема 2. Сума плоских кутів тригранного кута менша за 360°.

Ф 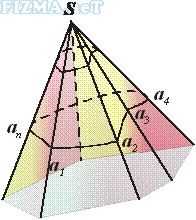ігура, що складається з усіх променів, які виходять із точки S і перетинають довільний многокутник, називають многогранним кутом.

Многогранний кут розбиває простір на дві області — внутрішню і зовнішню. Об’єднання многогранного кута з його внутрішньою областю також називають многогранним кутом.

Многогранний кут називається опуклим, якщо він розміщений з одного боку від площини кожної його грані.

Многогранний кут називають правильним, якщо між собою рівні всі його двогранні кути,а також рівні всі його плоскі кути.

Мірою многогранного кута називають різницю між сумою мір усіх його двогранних кутів і сумою мір внутрішніх кутів того многокутника, який утворюється в перерізі кута площиною, що перетинає всі його грані.

  1   2   3

скачати

© Усі права захищені
написати до нас