Ім'я файлу: Спектральный анализ непериодических сигналов.docx
Розширення: docx
Розмір: 92кб.
Дата: 24.04.2020
скачати
Розширення: docx
Розмір: 92кб.
Дата: 24.04.2020
скачати
Спектральный анализ непериодических сигналов
Пусть задан сигнал в виде ограниченной во времени функции S(t), отличной от нуля в промежутке t1t2 как показано на рис.2.
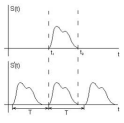
Рис.2 Пример непериодического сигнала
Выделим произвольный отрезок времени T, включающий промежуток t1t2, далее продолжим аналитически S(t) на всю бесконечную ось с периодом T. Тогда мы сможем разложить такую периодическую функцию S(t) в гармонический ряд Фурье. В комплексной форме будем иметь:
.Полученный ряд на участке [t1,t2] будет точно соответствовать нашей функции S(t). Однако, если нас интересуют моменты времени за участком [t1,t2], то необходимо увеличить период Т, т. е. отодвинуть повторные значения функции S(t). Производя замену переменных и переходя от суммирования к интегрированию, получим
, 
;
;
, 
, где
- спектральная плотность сигнала S(t).Спектр непериодического сигнала сплошной (непрерывный) и распространяется на отрицательные частоты.
Если S(ω) = A(ω) + iB(ω), то
- модуль спектральной плотности или амплитудно-частотная характеристика:
- фазово-частотная характеристика.Необходимое условие существования спектральной плотности:
.Рассмотрим непериодические сигналы при следующих ограничениях:
1. Функция ƒ(t) имеет конечное число max.
2. – существует.
Пусть имеется следующая функция:
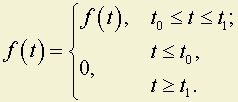
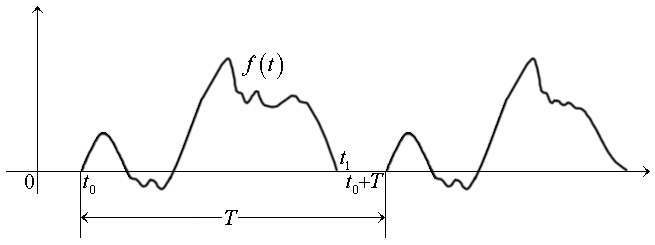
Рис. 10.7
Функция ƒ(t) – имеет конечную продолжительность по времени.
Если повторить ƒ(t), получим периодическую функцию:
ƒ1(t) = ƒ(t + T), ƒ1(t) = ƒ(t) при t0 ≤ t ≤ t0 + T.
Для ƒ1(t) можно дать спектральное описание:
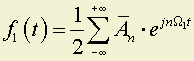
где
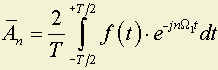.При T ® имеем:
;
;
;
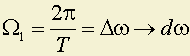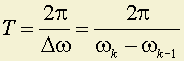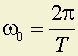,то есть
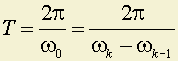.Обозначим
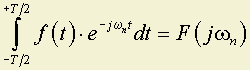,при T ® имеем:
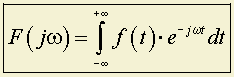.F(jω) – это прямое преобразование Фурье для ƒ(t).
Периодичность ƒ(t) уже не требуется.
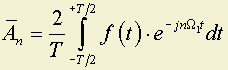
при T ® имеем:
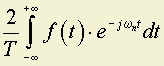,то есть для функции ограниченной длительности замена ±T/2 на ± не имеет значения, так как на всем остальном интервале ƒ(t) = 0.
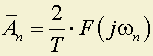,то есть для вычисления комплексной амплитуды любой гармоники периодической последовательности функций ƒ(t), т.е. ƒ1(t), достаточно вычислить F(jωn) непериодической функции, взять ее значение на частоте ωn = n · Ω и умножить на 2/T.
Подсчитаем теперь http://peredacha-informacii.ru/
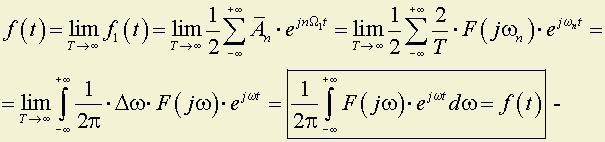
обратное преобразование Фурье для непериодической функции.
– модуль от преобразования Фурье назывется спектром.F(jω) – комплексная величина, которую можно записать в виде:
;
;
;
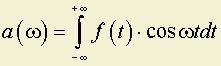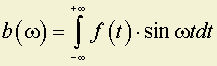,а
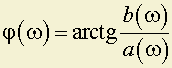,где F(ω) – спектр амплитуд;
φ(ω) – спектр фаз.
Обратное преобразование Фурье может быть записано:
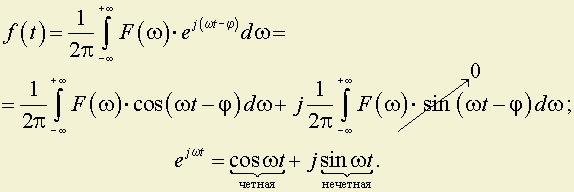
sin(ωt – φ) – нечетная функция ω;
cos(ωt – φ) – четная функция ω.
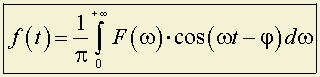–другая запись преобразования Фурье.