
| Ім'я файлу: Пар 9-3 Ознаки зб_жност_ ряду Фур'є.doc Розширення: docРозмір: 221кб.Дата: 17.12.2021скачати
Глава 9
Ряд та інтеграл Фур’є
3.Ознаки збіжності ряду Фур’є
Тут і далі через 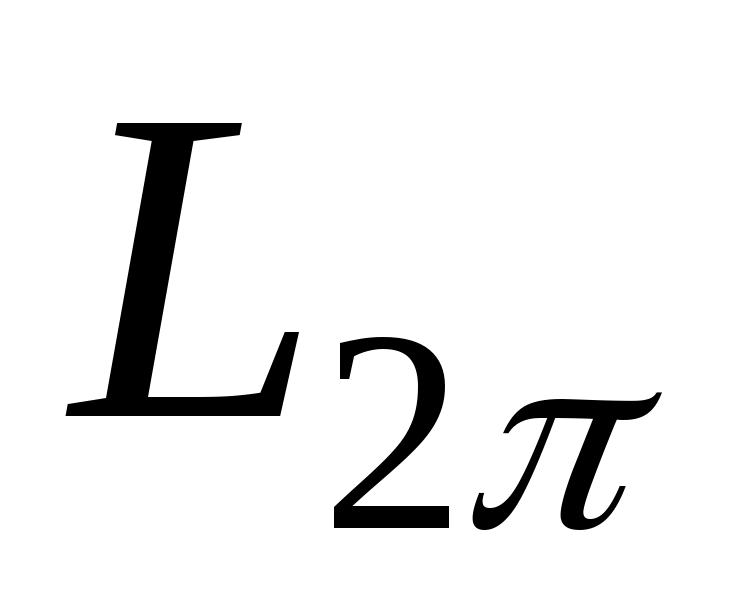 будемо позначати клас усіх будемо позначати клас усіх 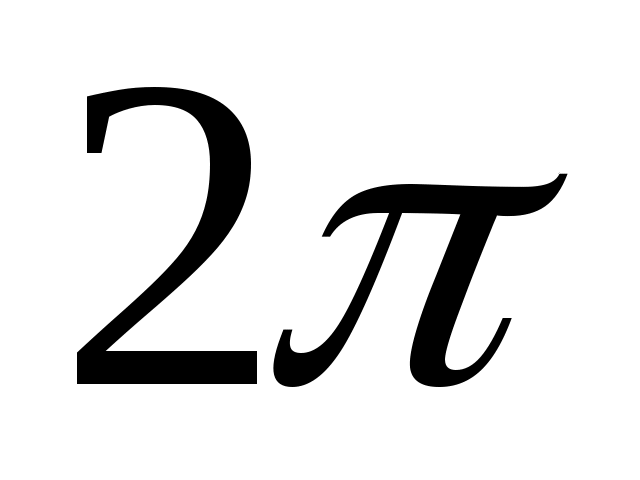 - періодичних функцій, інтегрованих за Ріманом на проміжку - періодичних функцій, інтегрованих за Ріманом на проміжку 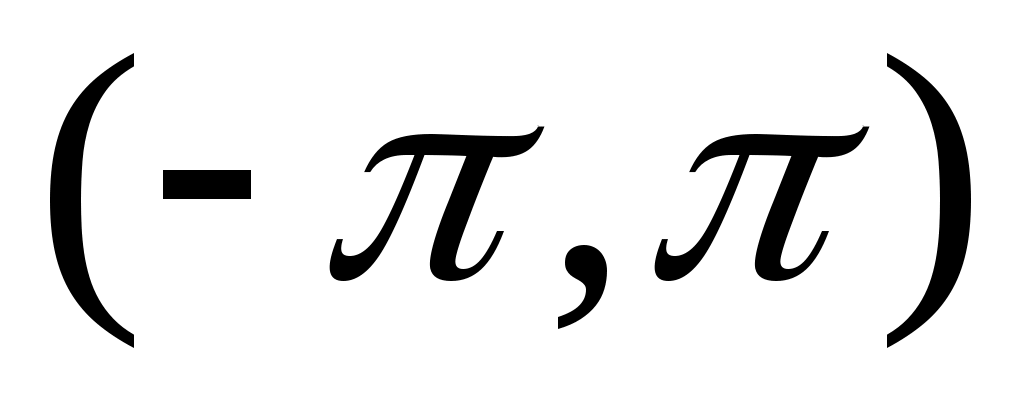 , і тим самим на будь-якому скінченому проміжку. , і тим самим на будь-якому скінченому проміжку.
Теорема 1.
|
(Діріхле)
|
|
Якщо  , тоді , тоді
|
|
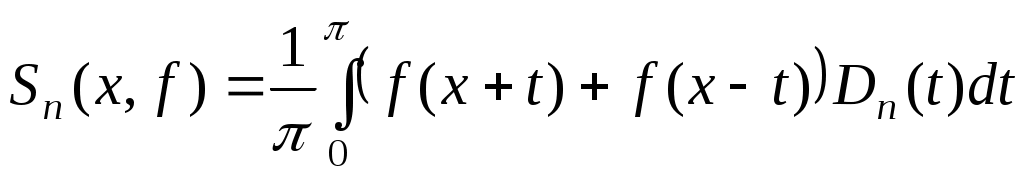 , ,
|
(1)
|
|
де 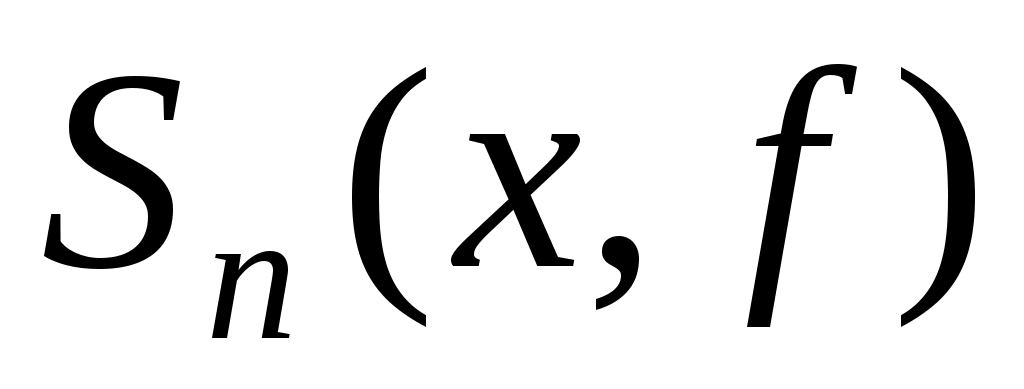 є частковою сумою ряду Фур’є функції є частковою сумою ряду Фур’є функції 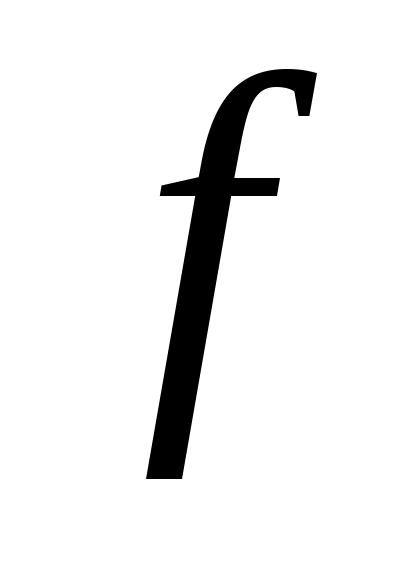 в точці в точці 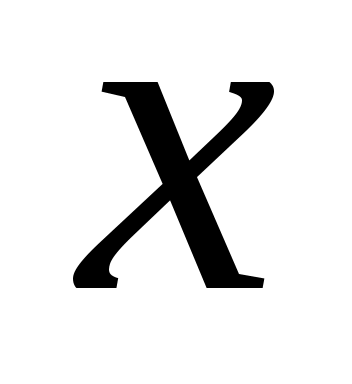 , де , де
|
|

|
(2)
|
|
називається ядром Діріхле.
|
Доведення. 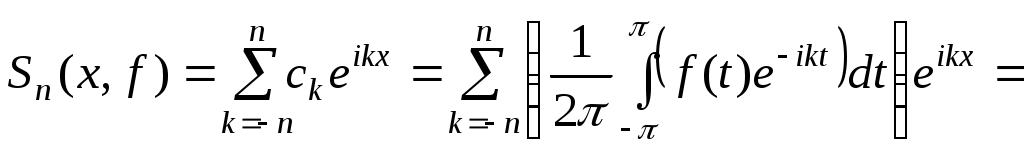 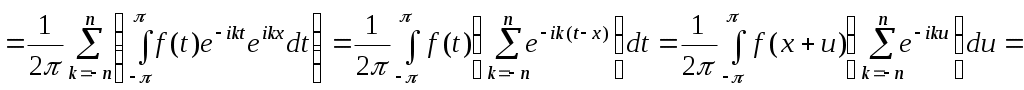 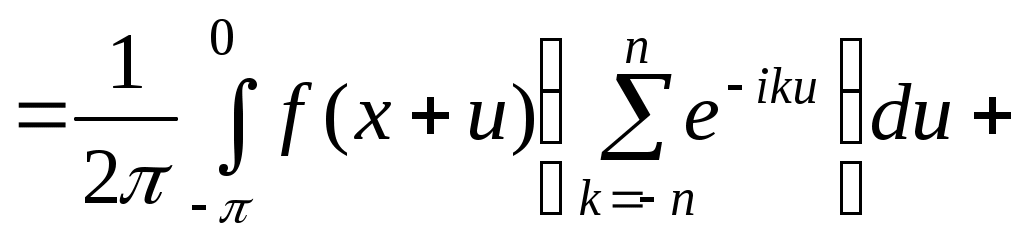 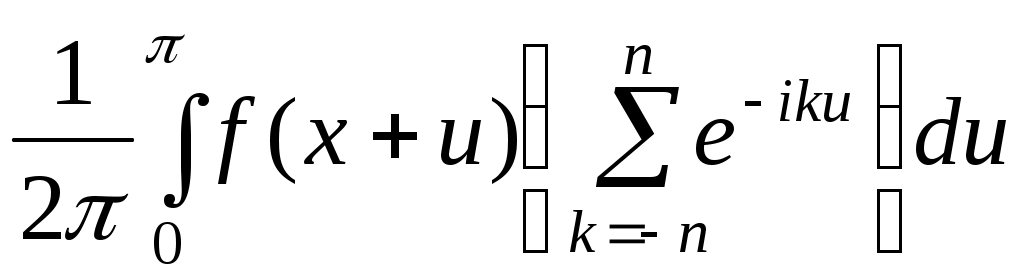 
в першому інтегралі робимо заміну 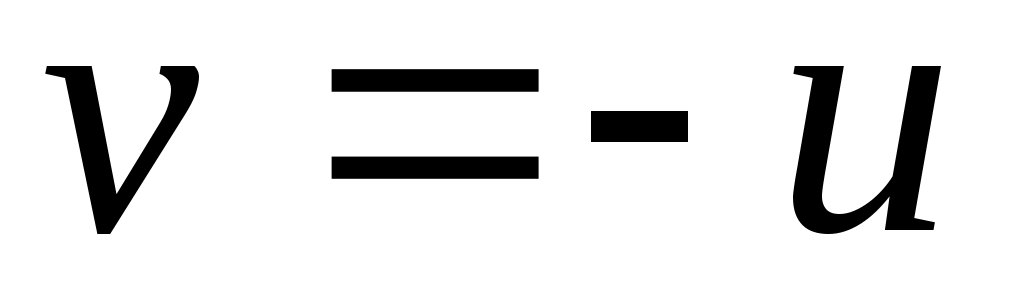 , тоді одержимо в продовженні: , тоді одержимо в продовженні:
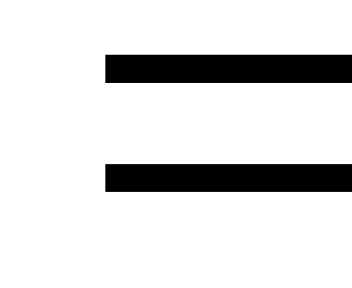  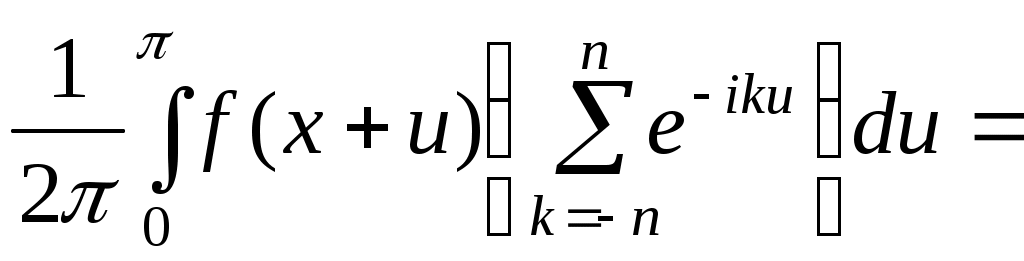 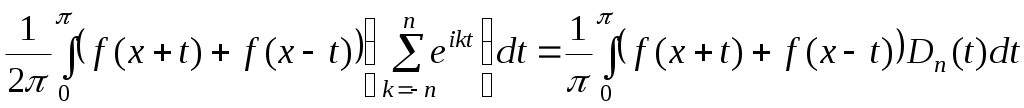 , де , де
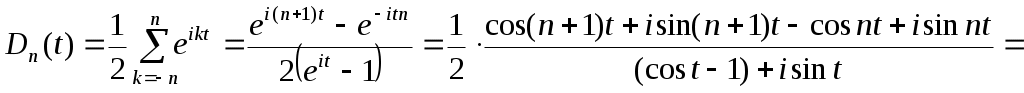 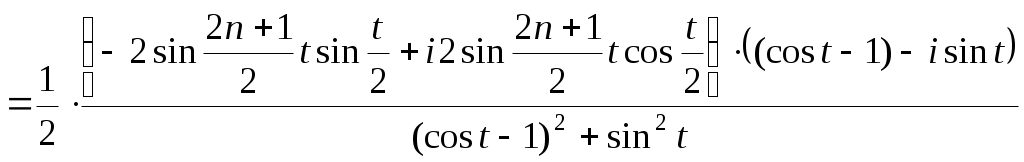 
тепер будемо збирати лише дійсну частину виразу, оскільки ліва частина дійсна
  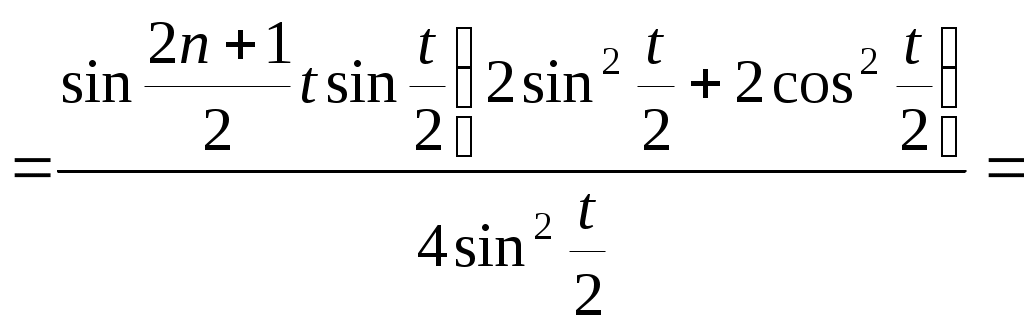 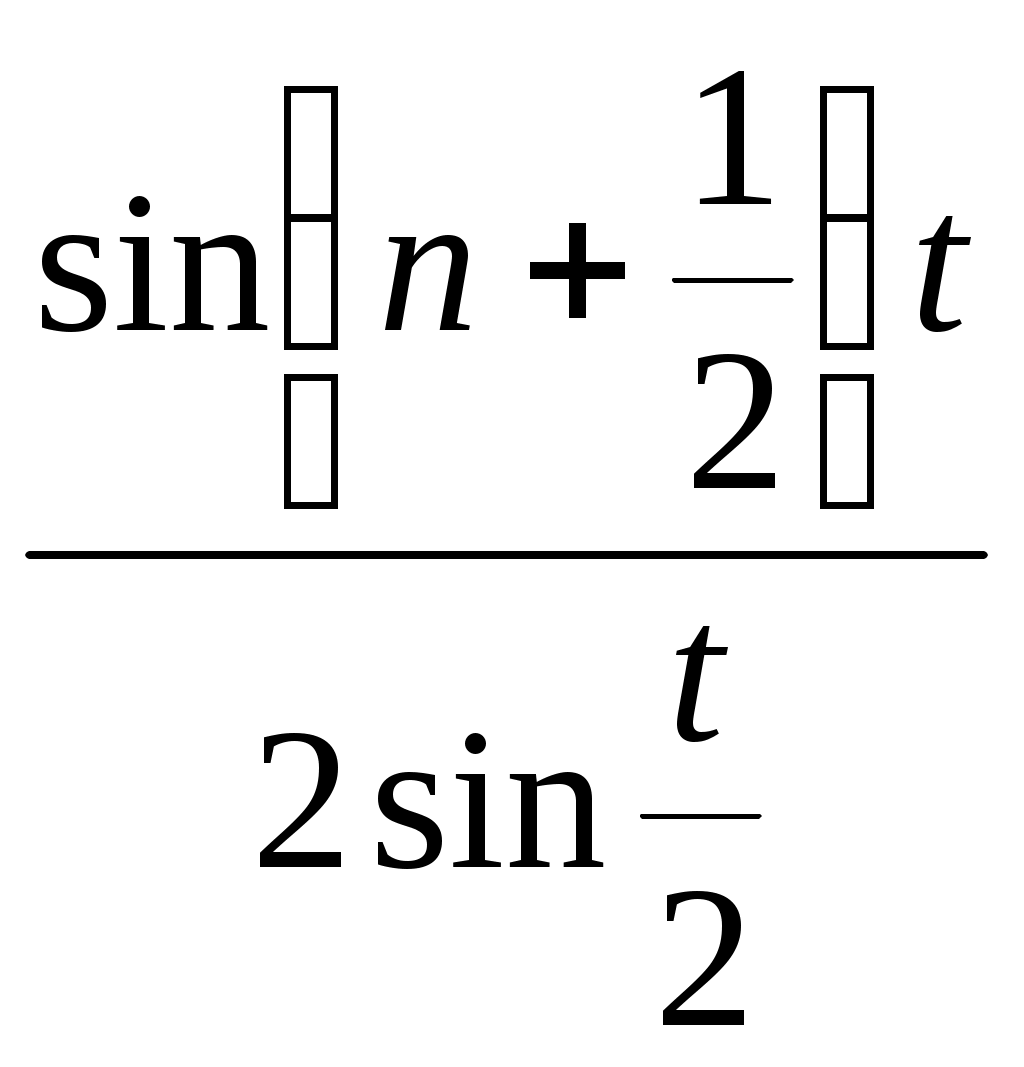 , що й треба було довести. , що й треба було довести.
Теорема доведена.
Теорема 2.
|
(Принцип локалізації Рімана)
|
|
Нехай  , тоді , тоді 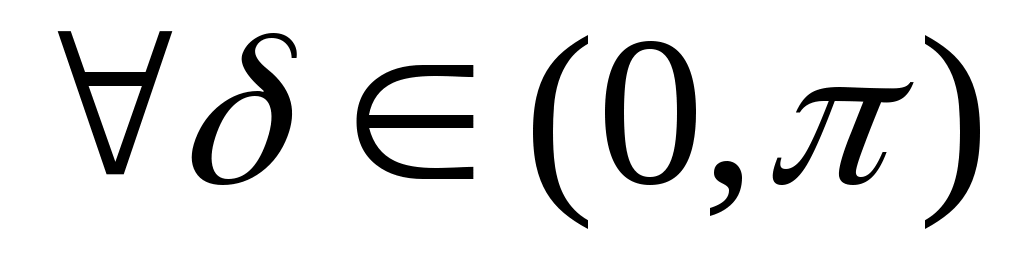 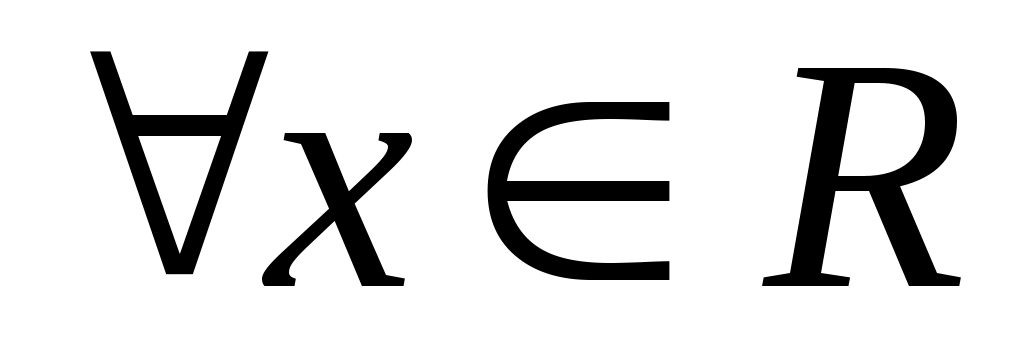 існує така нескінченно мала послідовність існує така нескінченно мала послідовність 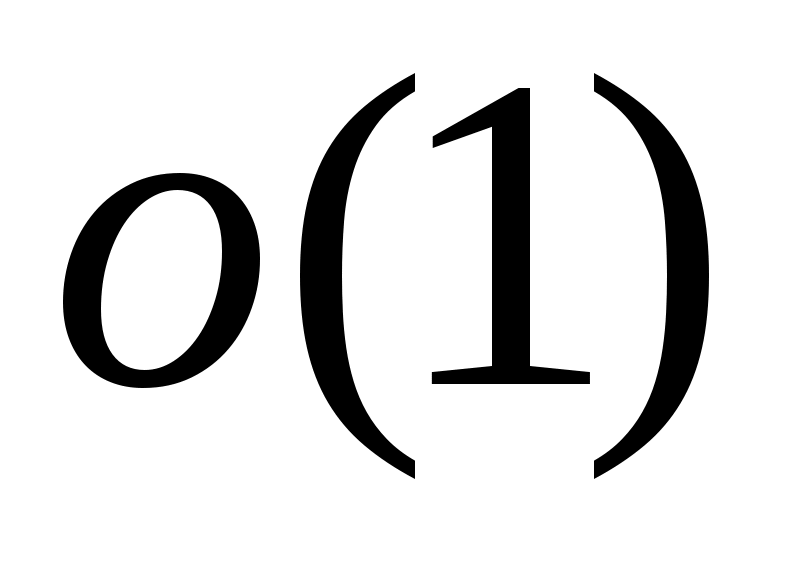 , що залежить від , що залежить від 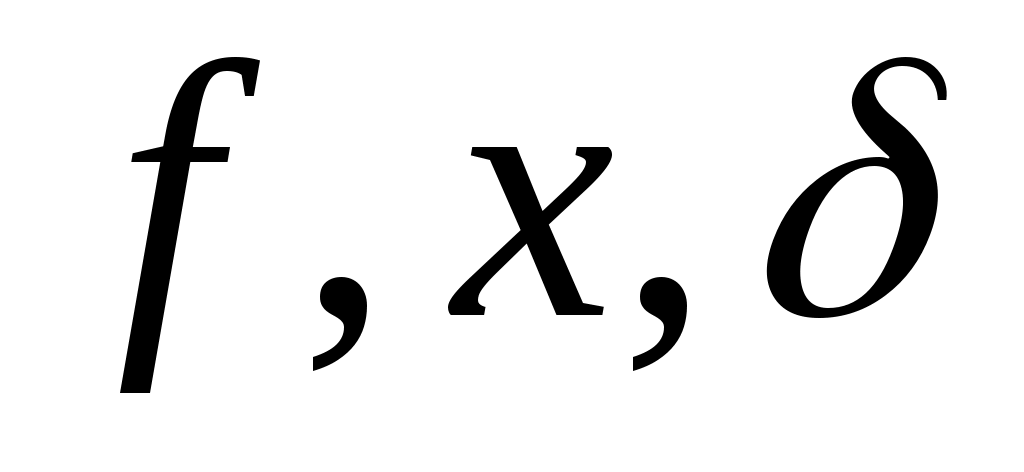 , що , що
|
|
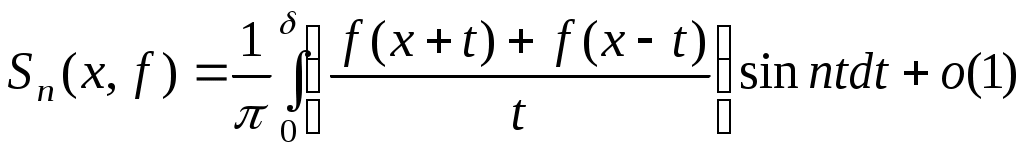 . .
|
(3)
|
Доведення. Нехай 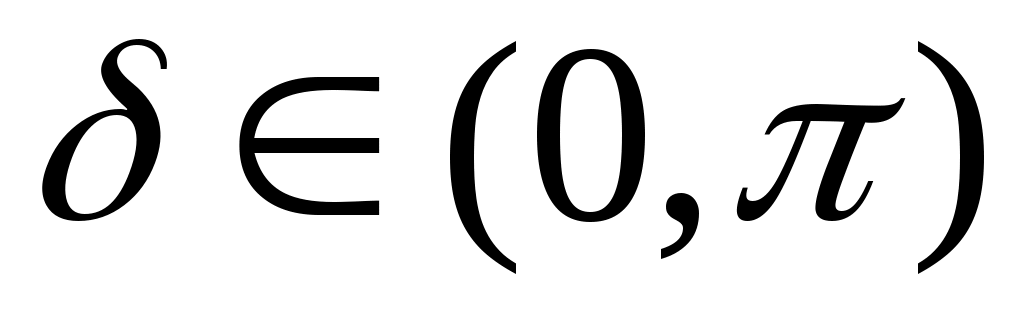 . Враховуючи тотожність . Враховуючи тотожність
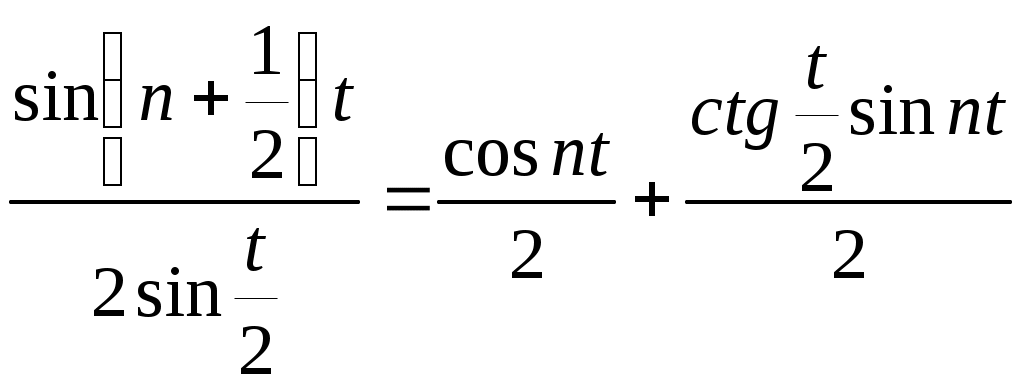 і формулу (3) можемо записати рівність: і формулу (3) можемо записати рівність:
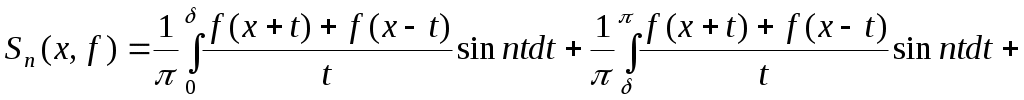 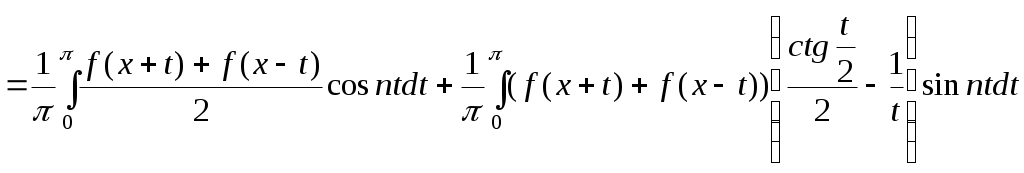 . (4) . (4)
Оскільки 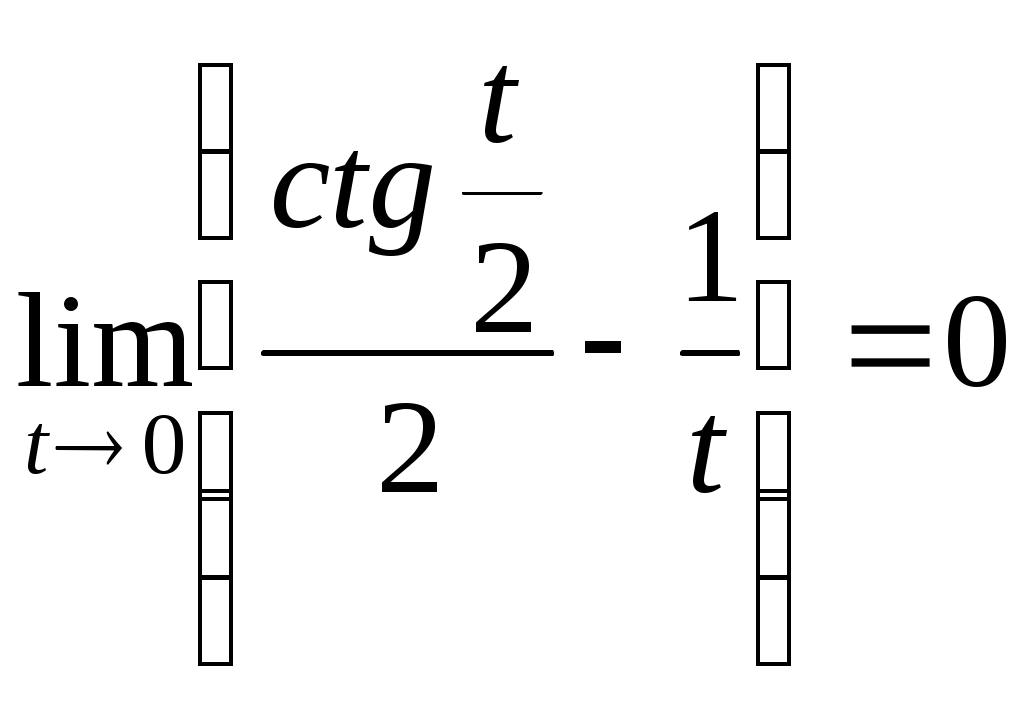 , то ця функція обмежена при , то ця функція обмежена при 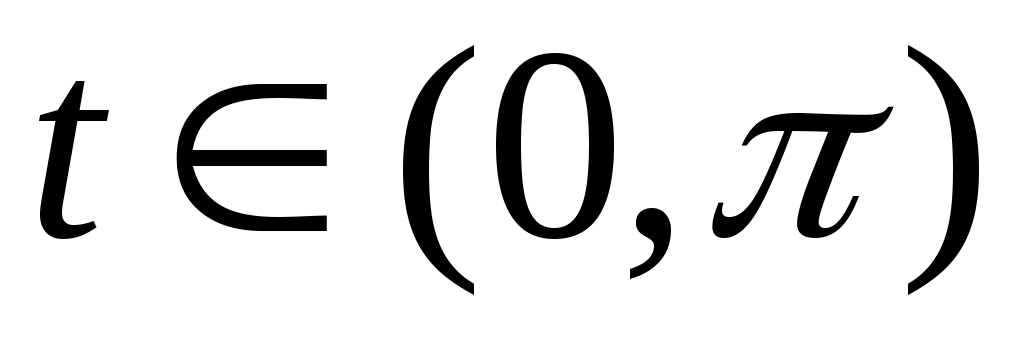 . Тому в формулі (4) усі інтеграли крім першого є синус та косинус перетвореннями Фур’є деяких функцій (ці функції треба продовжити нулем на всю дійсну вісь, крім вказаного проміжку), а тому з наслідку з теореми Рімана-Лебега прямують до нуля при . Тому в формулі (4) усі інтеграли крім першого є синус та косинус перетвореннями Фур’є деяких функцій (ці функції треба продовжити нулем на всю дійсну вісь, крім вказаного проміжку), а тому з наслідку з теореми Рімана-Лебега прямують до нуля при  , саме їх сума і дає нам шукану нескінченно малу послідовність , саме їх сума і дає нам шукану нескінченно малу послідовність 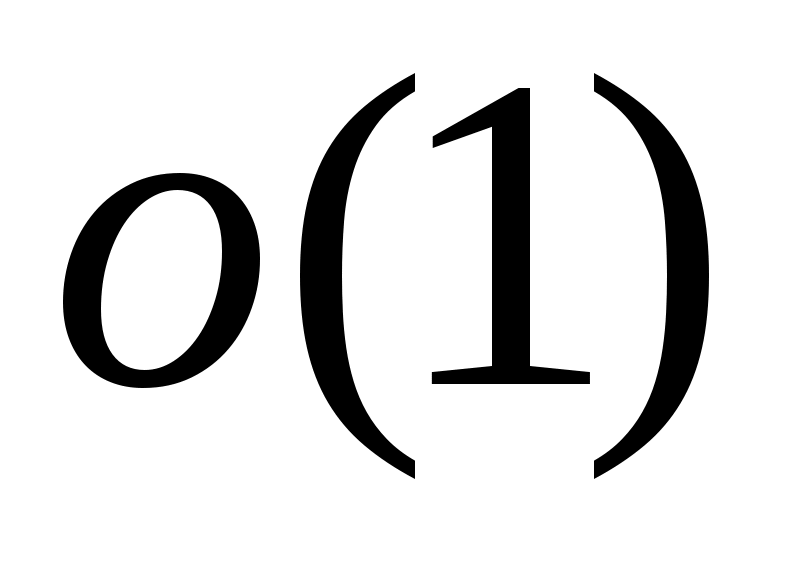 . .
Теорема доведена.
Теорема 3.
|
(Ознака Діні)
|
|
Нехай  . Якщо існують такі . Якщо існують такі 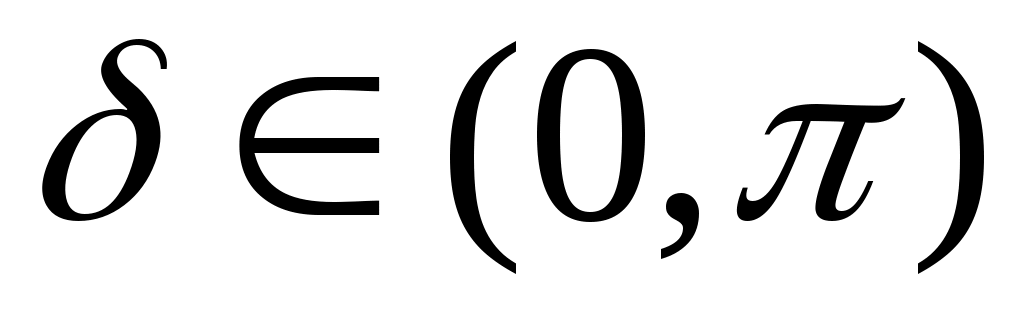 і функція і функція 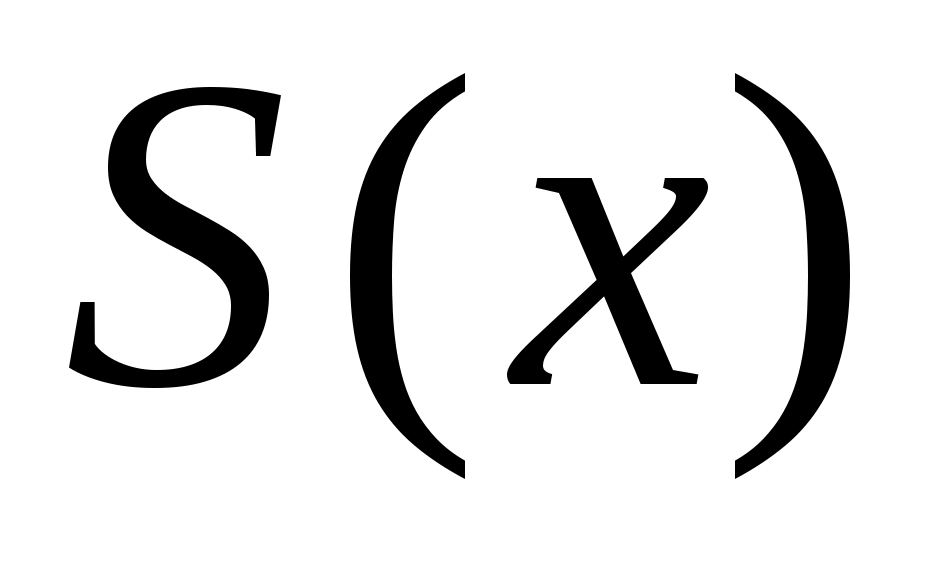 така, що така, що
|
|
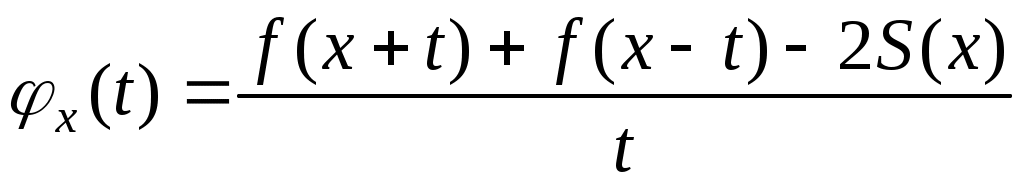
|
(5)
|
|
Інтегрована за Ріманом на 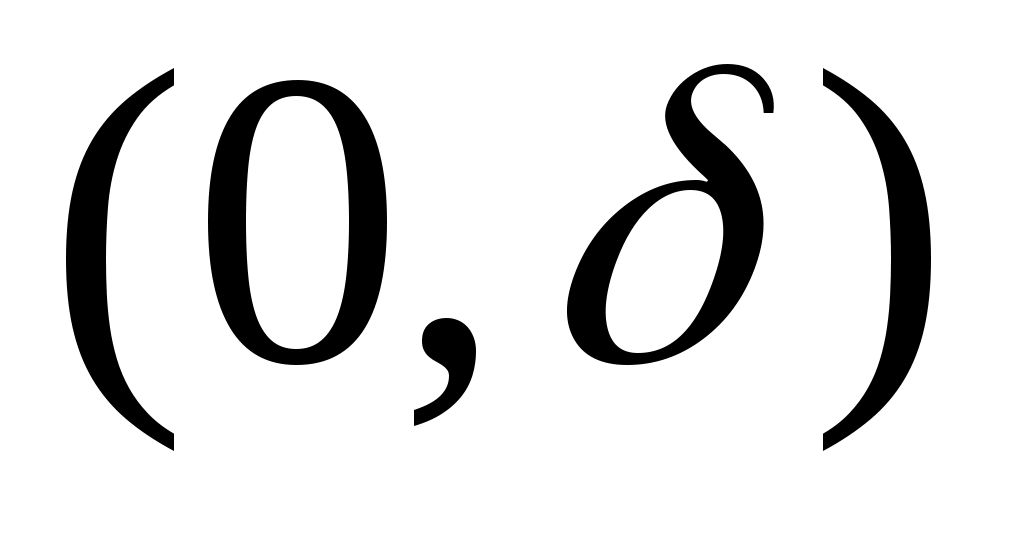 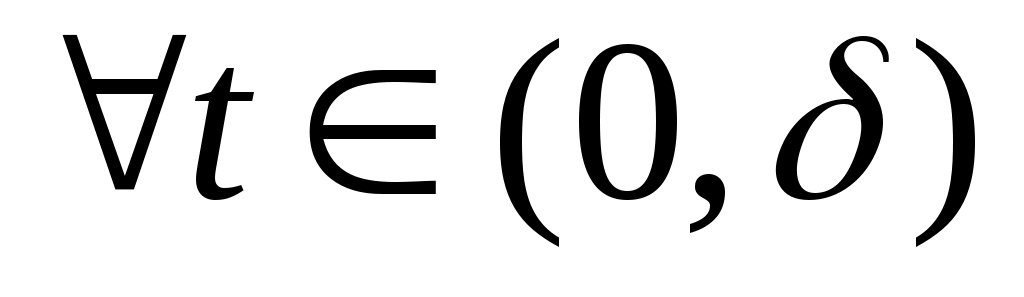 , то РФ функції , то РФ функції 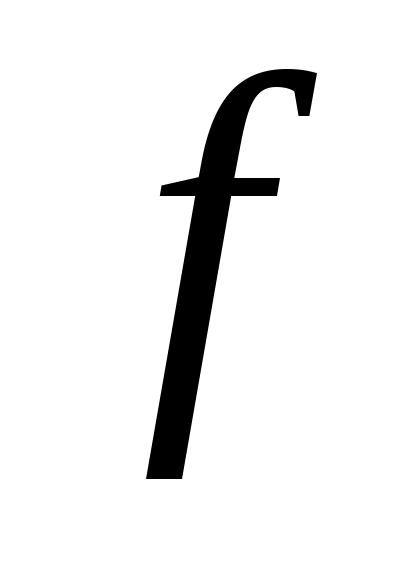 збігається до збігається до 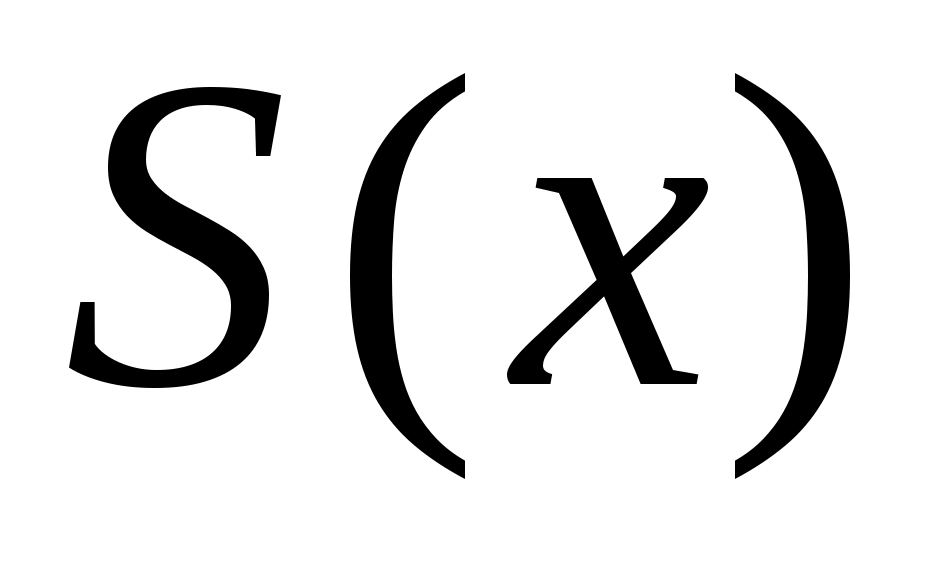 в точці в точці 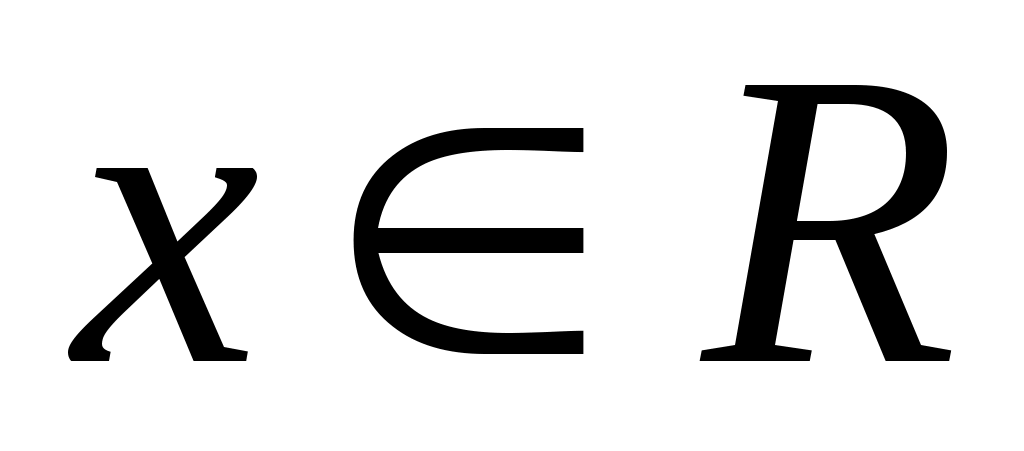 . .
|
Доведення. Покладемо в теоремі 2 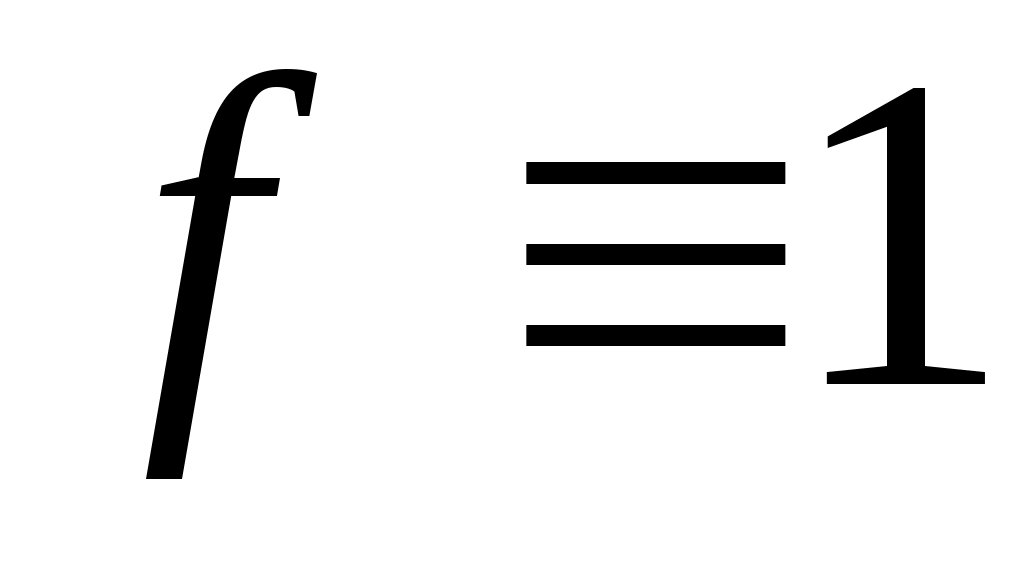 , тоді одержимо таке співвідношення: , тоді одержимо таке співвідношення:
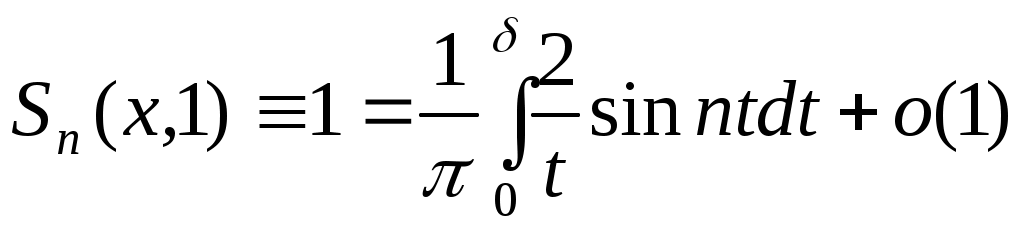  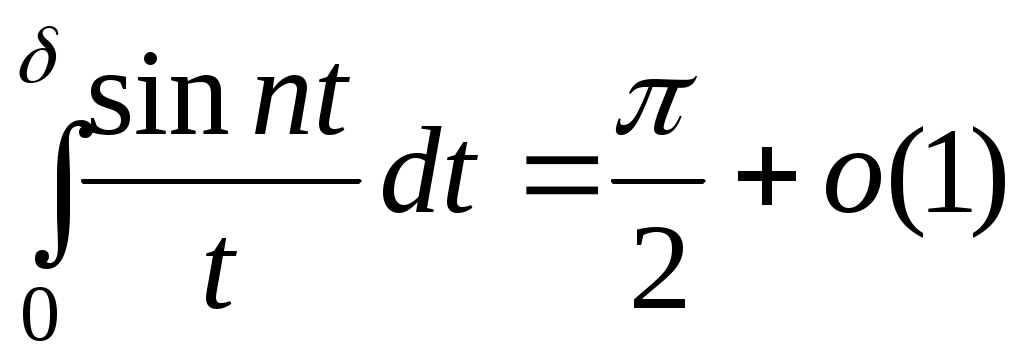 . Далі з принципу локалізації маємо: . Далі з принципу локалізації маємо: 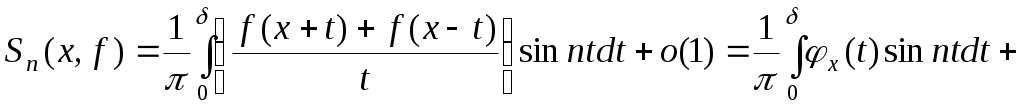 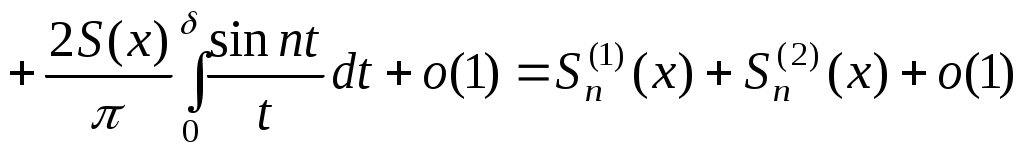 . З наслідку теореми Рімана-Лебега . З наслідку теореми Рімана-Лебега 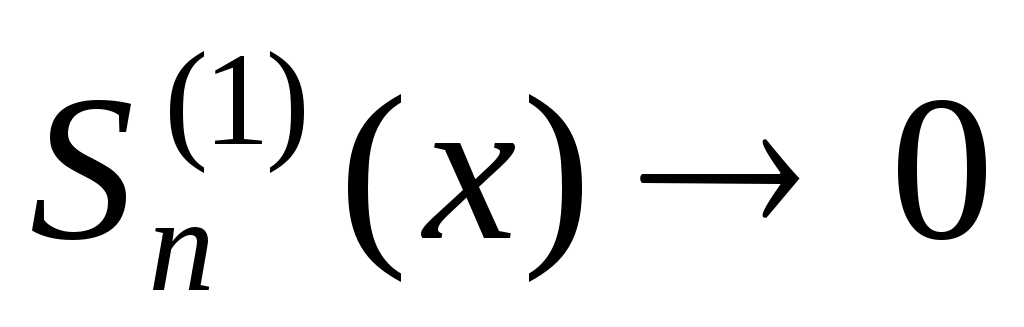 при при  , а , а 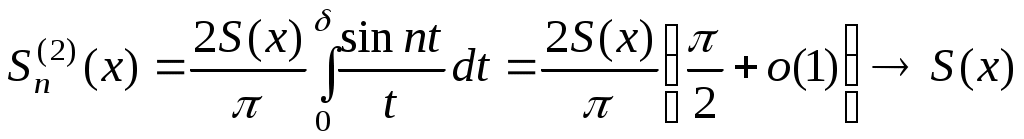 , що й треба було довести. , що й треба було довести.
Теорема доведена.
Функція 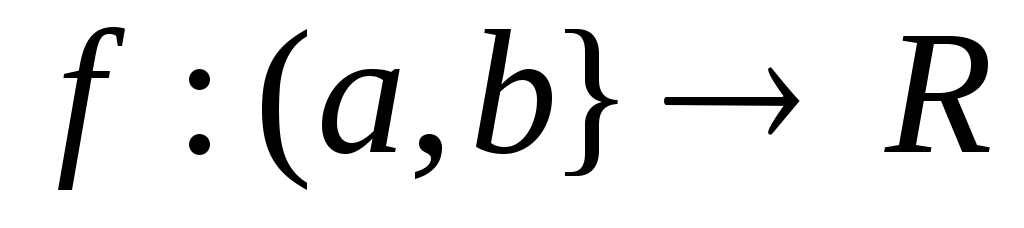 задовольняє умову Ліпшиця порядку задовольняє умову Ліпшиця порядку 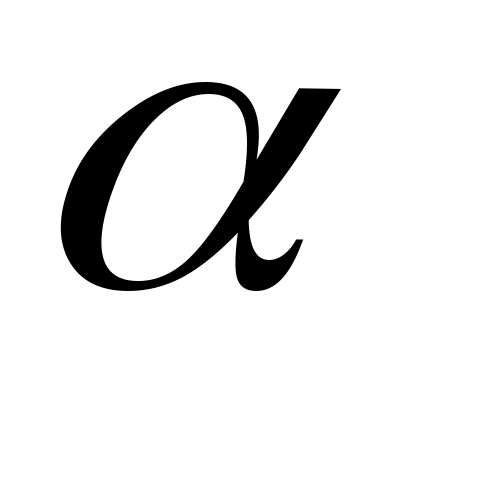 з сталою з сталою  в точці в точці 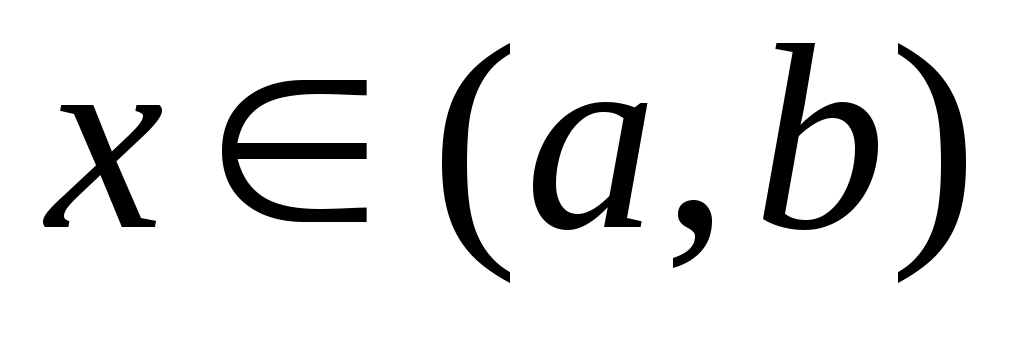 , якщо , якщо 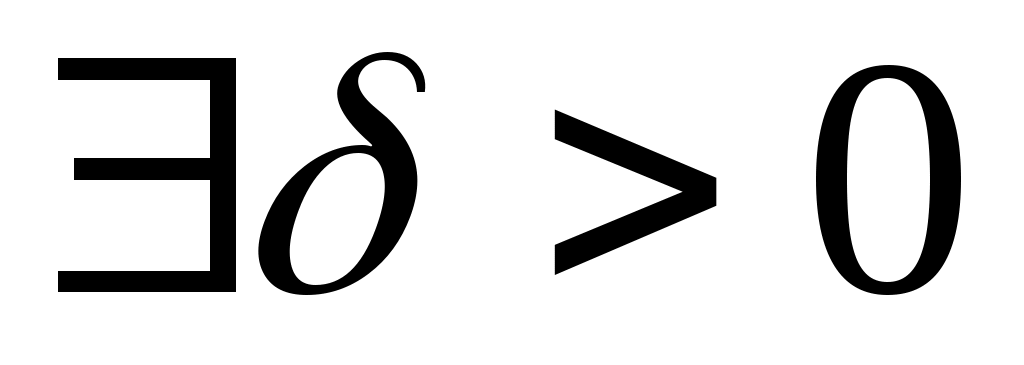 : : 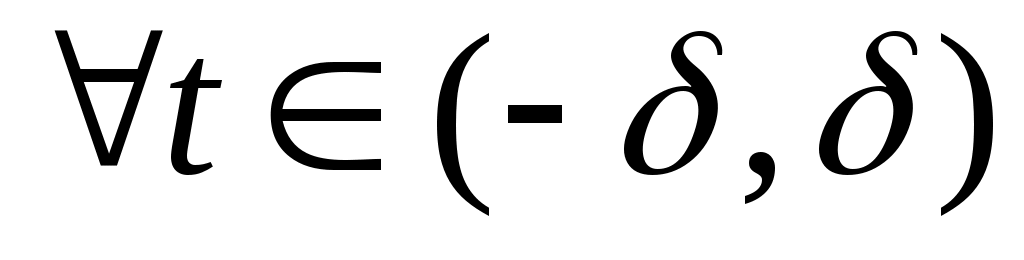 виконується нерівність: виконується нерівність:
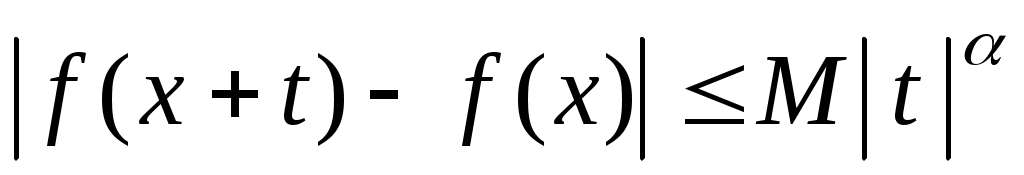 (7) (7)
Теорема 4.
|
(Ознака Ліпшиця)
|
|
Нехай  . Якщо в точці . Якщо в точці 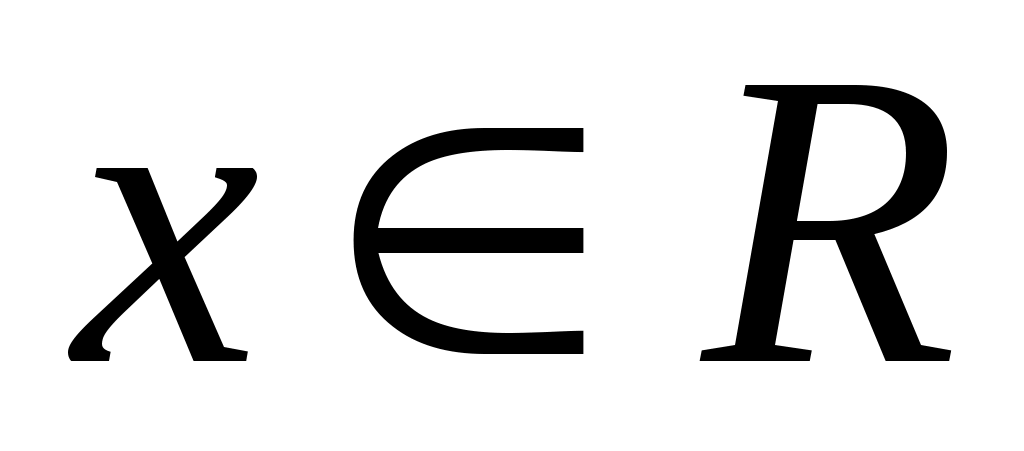 виконується умова Лівшиця деякого порядку виконується умова Лівшиця деякого порядку  , то РФ функції , то РФ функції 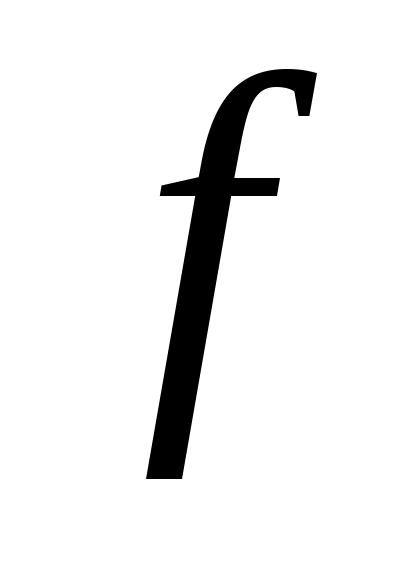 збігається в цій точці до значення збігається в цій точці до значення  . .
|
Доведення. В умовах ознаки Діні покладемо в якості 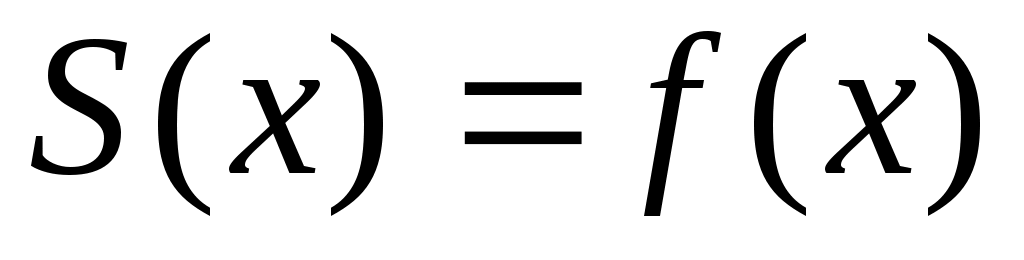 . Оскільки . Оскільки 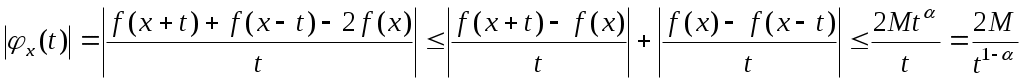 , то при , то при  параметр параметр 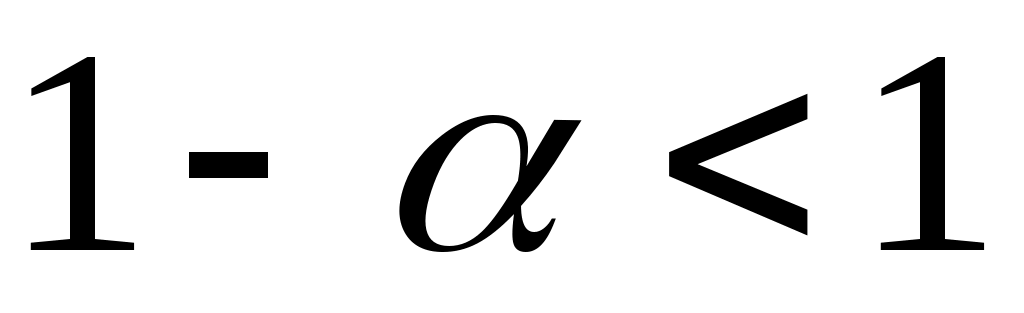 , а тому , а тому 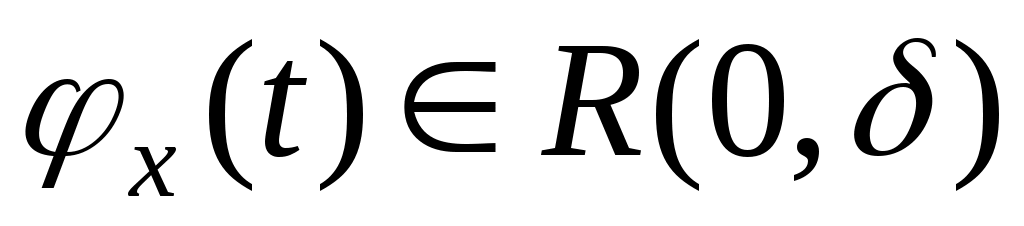 , а тому з ознаки Діні , а тому з ознаки Діні 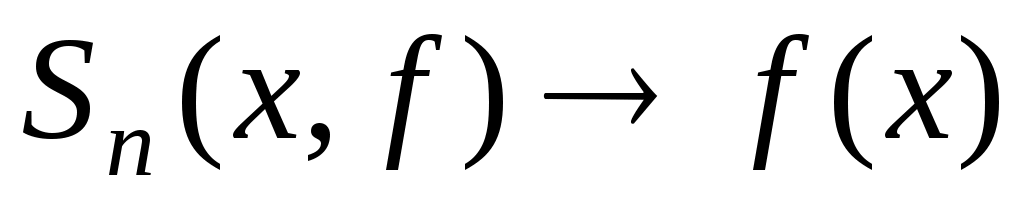 при при  . .
Теорема доведена.
Наслідок 1.
|
(РФ диференційованої функції)
|
|
Якщо  і в точці і в точці 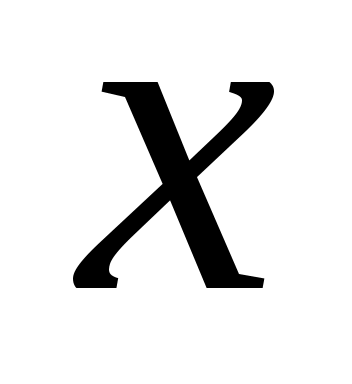 існує похідна існує похідна 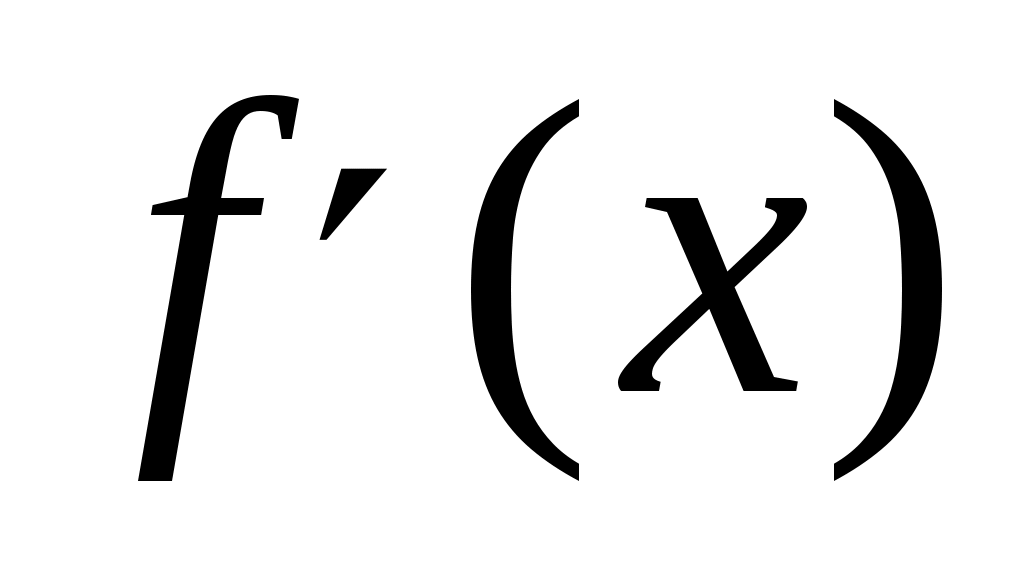 , то РФ функції , то РФ функції 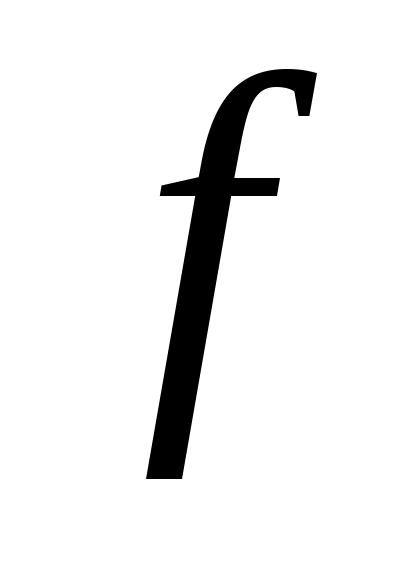 збігається в точці збігається в точці 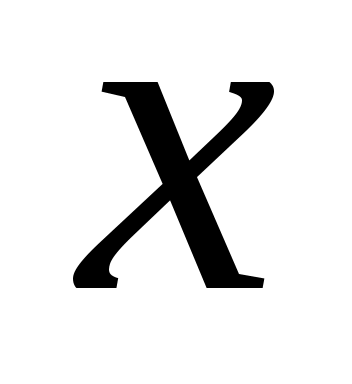 до значення до значення  . .
|
Доведення. З існування похідної слідує існування границі  , а тому в деякому , а тому в деякому 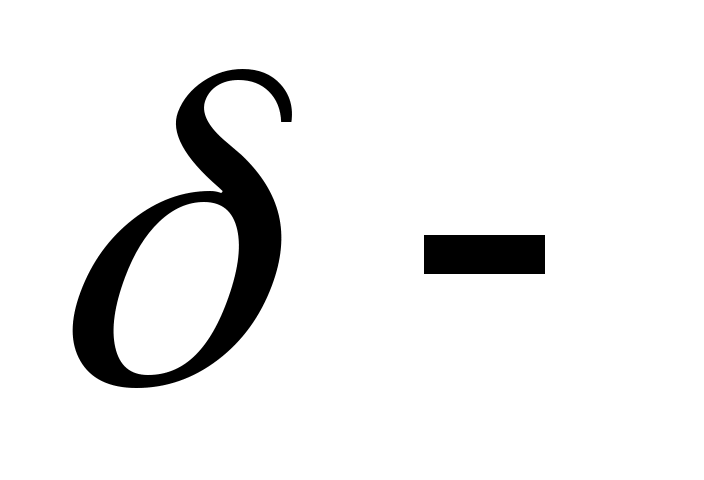 околі точки околі точки 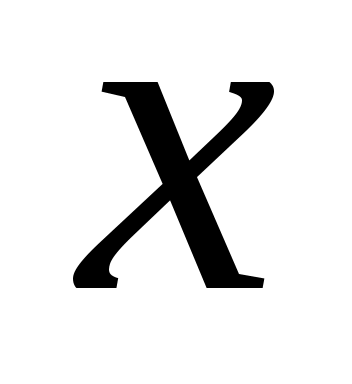 виконується нерівність виконується нерівність  (при (при 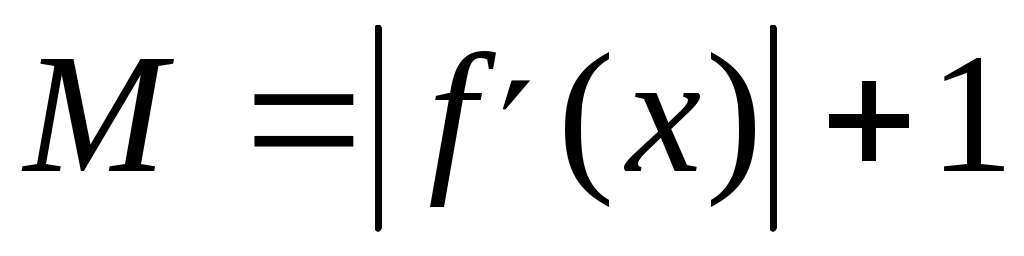 ), що відповідає виконанню умови Ліпшиця з порядком ), що відповідає виконанню умови Ліпшиця з порядком 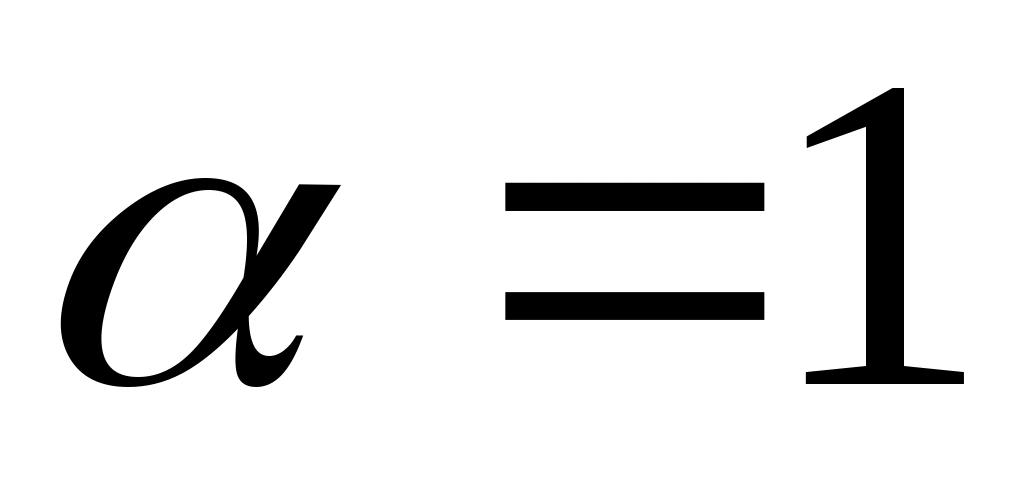 . .
Наслідок доведено.
Наслідок 2.
|
(РФ функції з узагальненими похідними)
|
|
Якщо  і в точці і в точці 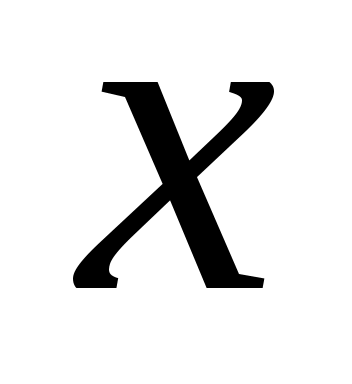 існують обидві узагальнені похідні існують обидві узагальнені похідні 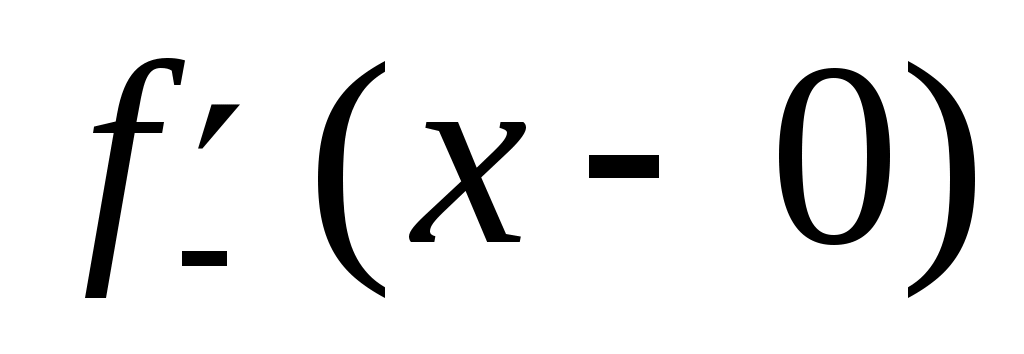 , , 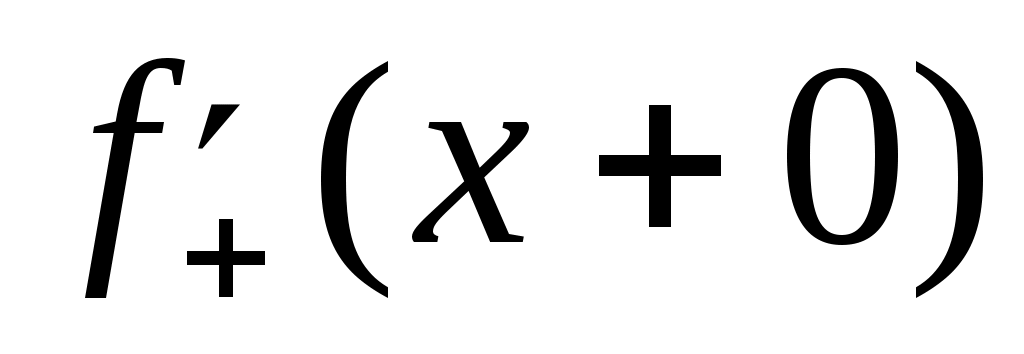 , то РФ функції , то РФ функції 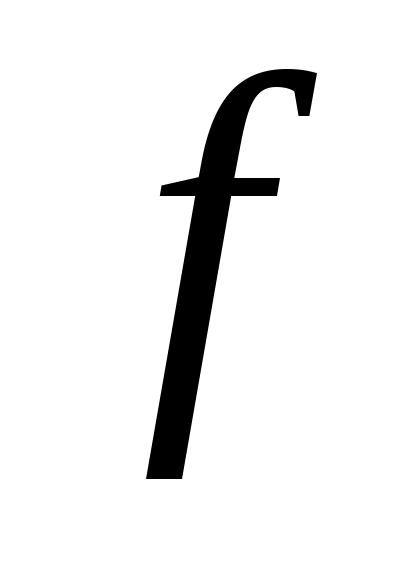 збігається в точці збігається в точці 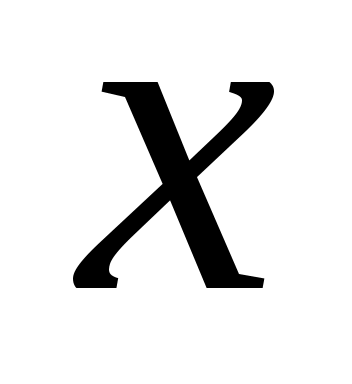 до значення до значення 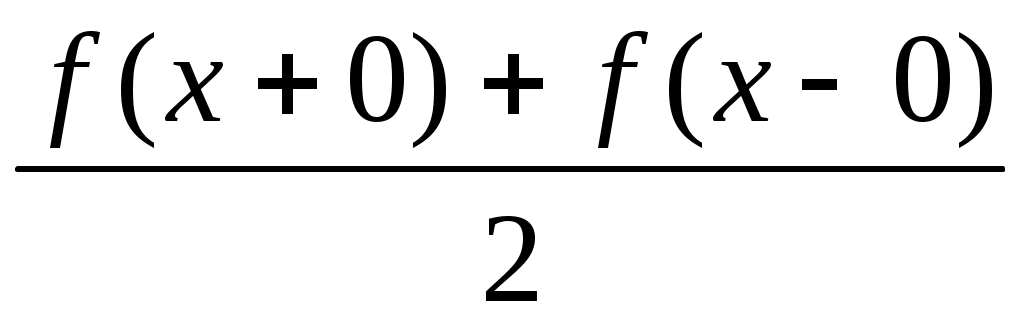 . .
|
Доведення. Нагадаємо означення узагальнених похідних:
 , , 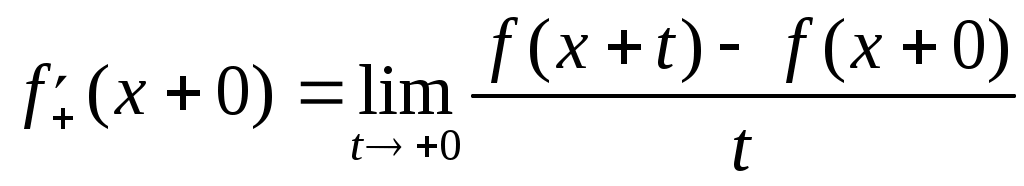 , вони узагальнюють поняття лівосторонньої та правосторонньої похідних у точці. Якщо останні існують, то вони зрозуміло, що співпадають з узагальненими відповідними похідними. Для доведення наслідку достатньо в ознаці Діні покласти , вони узагальнюють поняття лівосторонньої та правосторонньої похідних у точці. Якщо останні існують, то вони зрозуміло, що співпадають з узагальненими відповідними похідними. Для доведення наслідку достатньо в ознаці Діні покласти 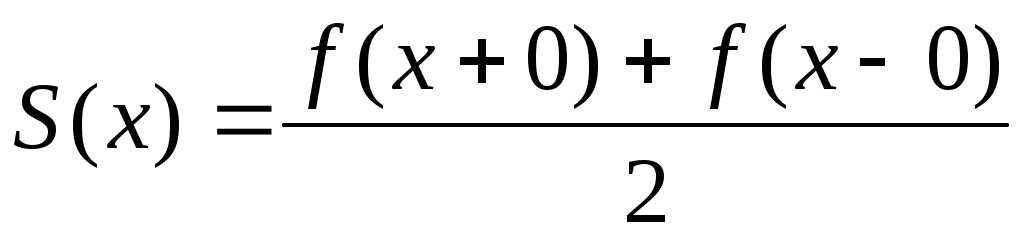 , а далі все просто. , а далі все просто.
Наслідок доведено.
Наслідок 2.
|
(РФ кусково гладкої функції)
|
|
Якщо  є кусково гладкою на проміжку є кусково гладкою на проміжку 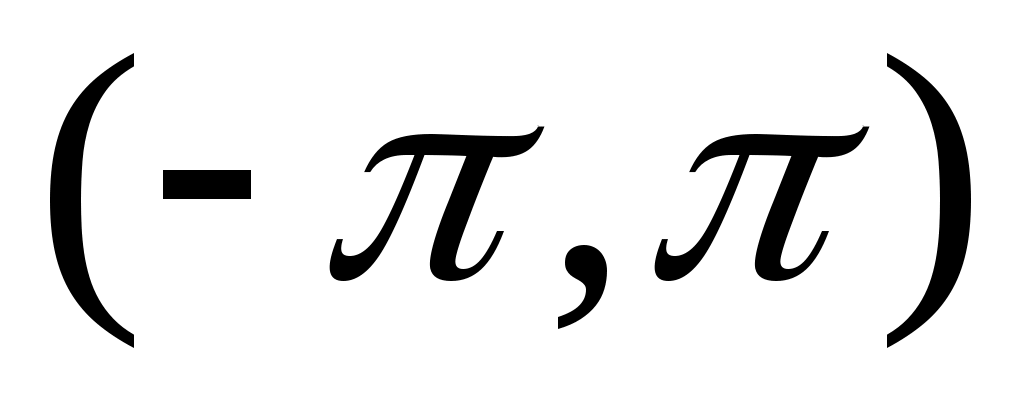 , то РФ функції , то РФ функції 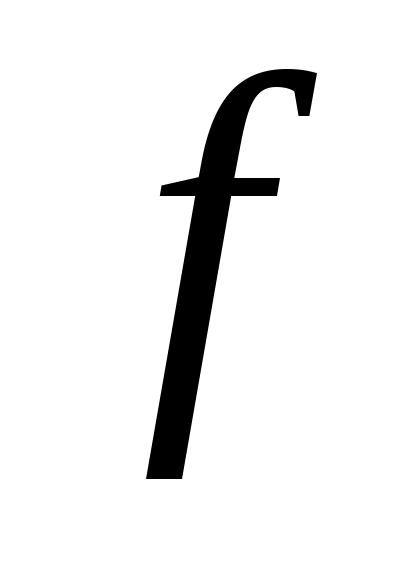 збігається в точці збігається в точці 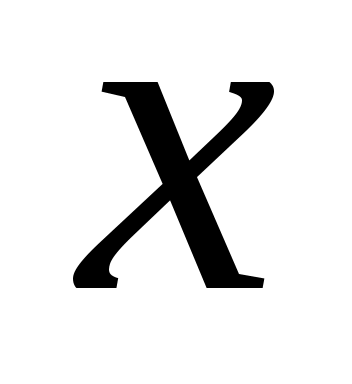 до значення до значення 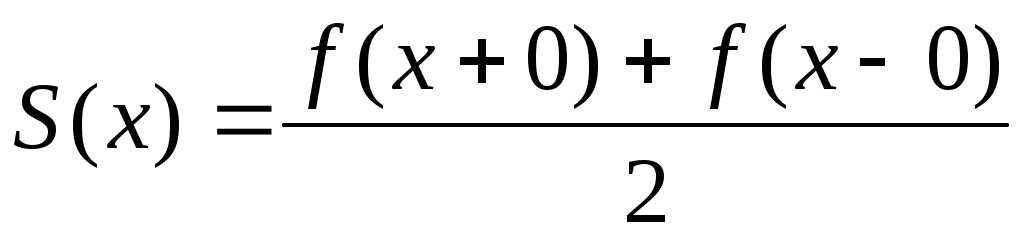 , тобто в точці неперервності функції , тобто в точці неперервності функції 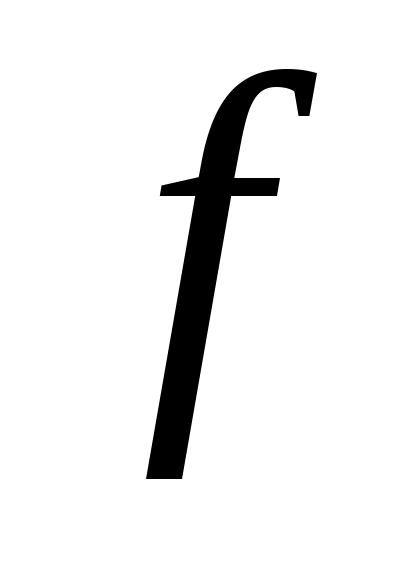 РФ збігається до РФ збігається до  , а в точці розриву першого роду до середнього арифметичного границь на краях. , а в точці розриву першого роду до середнього арифметичного границь на краях.
|
Безпосередньо слідує з попереднього наслідку.
скачати
|


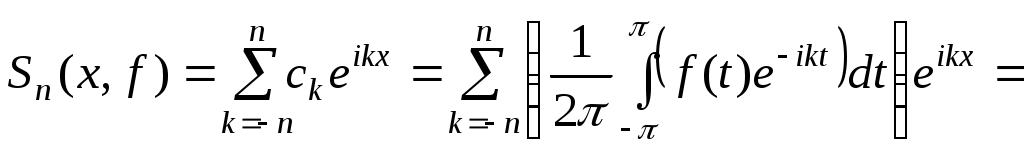
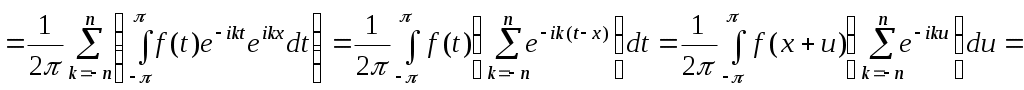
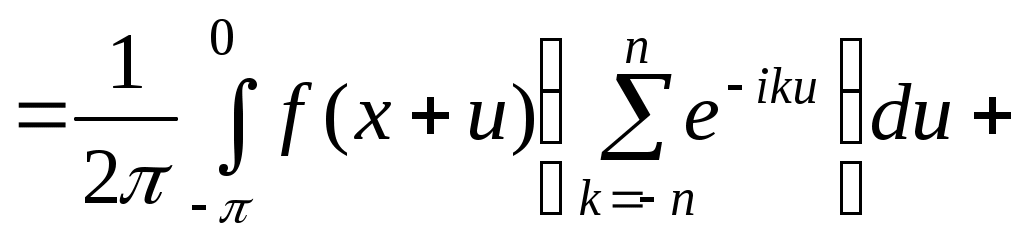
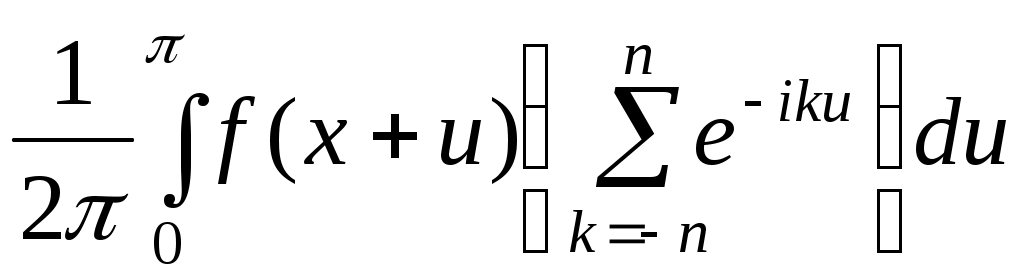

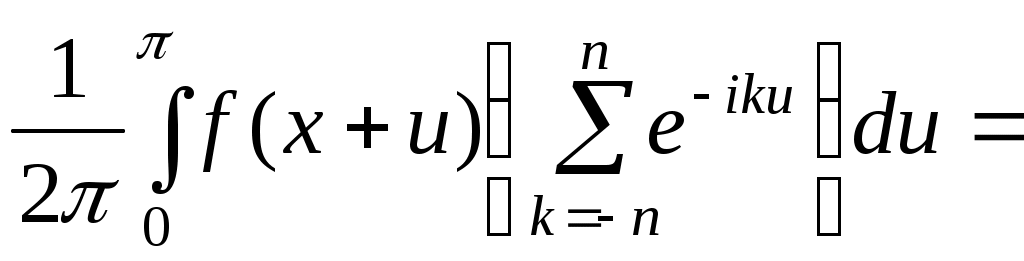
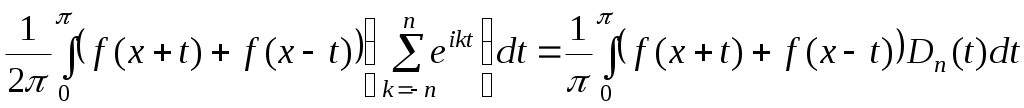 , де
, де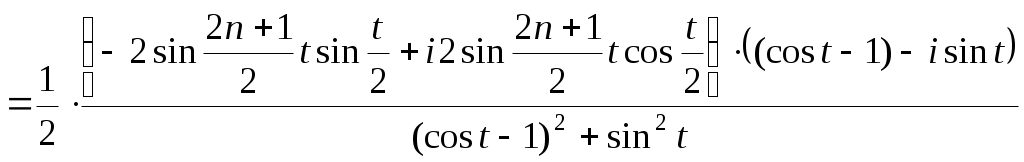

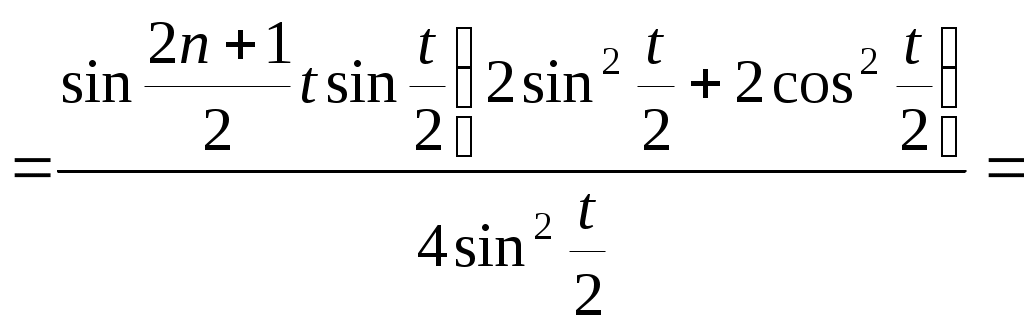
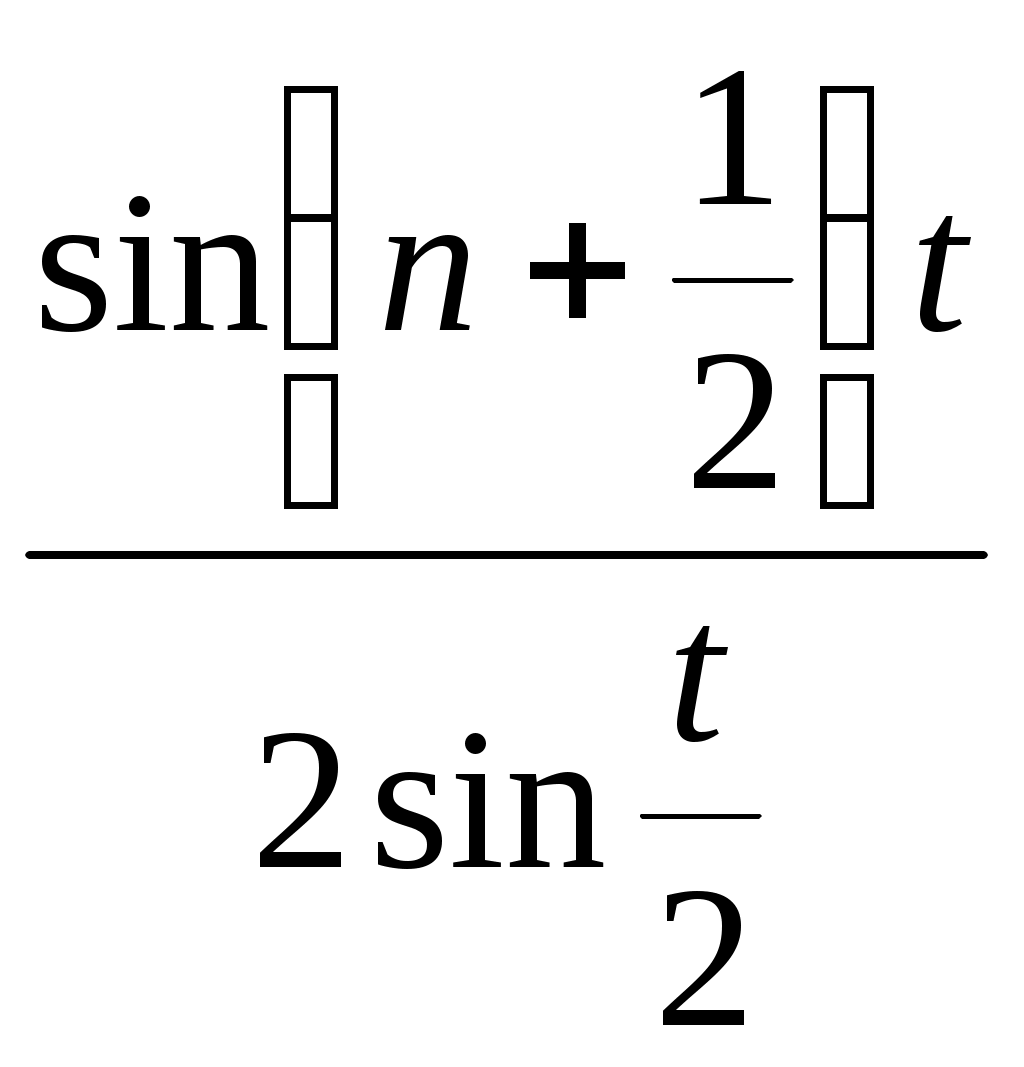 , що й треба було довести.
, що й треба було довести.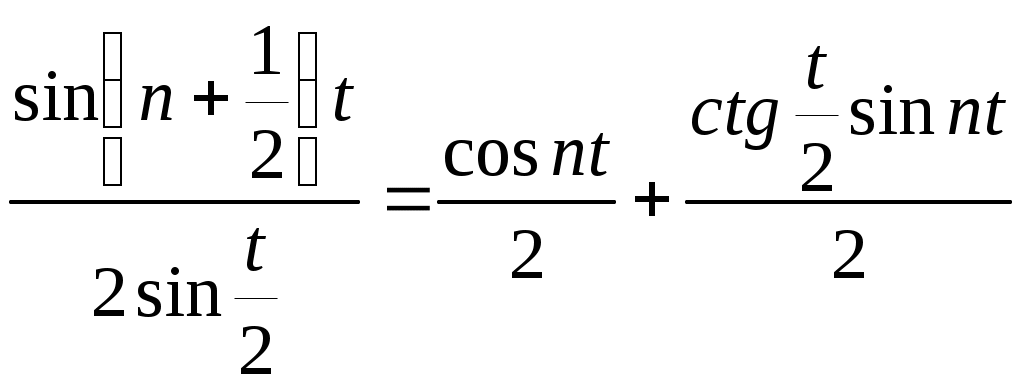 і формулу (3) можемо записати рівність:
і формулу (3) можемо записати рівність: 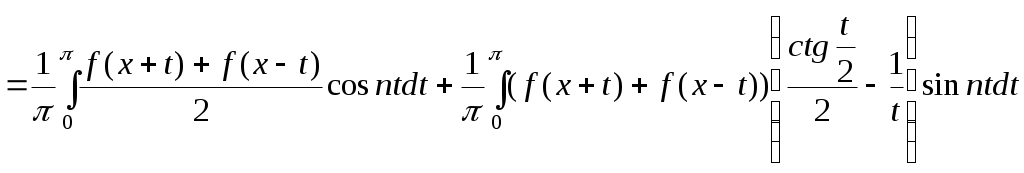 . (4)
. (4)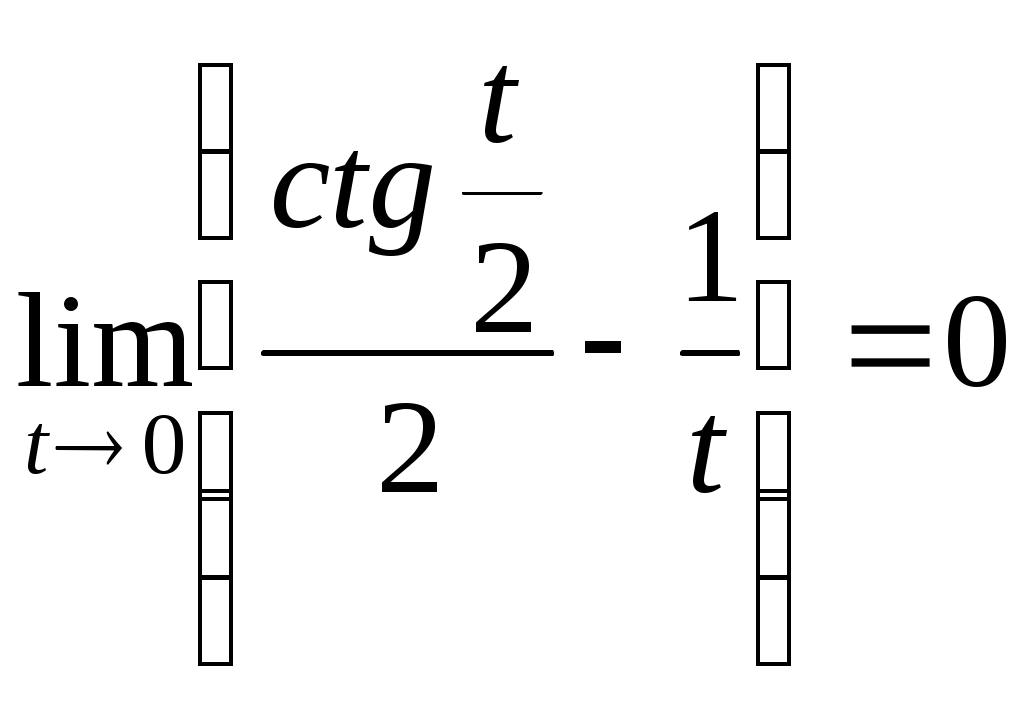 , то ця функція обмежена при
, то ця функція обмежена при