
Ім'я файлу: Розвиток поняття про число в шкільному курсі математики.docx
Розширення: docx
Розмір: 169кб.
Дата: 24.11.2020
скачати
Розширення: docx
Розмір: 169кб.
Дата: 24.11.2020
скачати
НАЦІОНАЛЬНИЙ ПЕДАГОГІЧНИЙ УНІВЕРСИТЕТ ІМЕНІ М.П.ДРАГОМАНОВА
Кафедра математики і теорії та методики навчання математики
КУРСОВА РОБОТА
з методики навчання математики
на тему: Розвиток поняття про число в ШКМ
Студентки
Курінної Т.В.
Керівник:
Сазонова О.П.
Київ – 2017
Зміст
Вступ
1. Історія виникнення чисел та поняття числа
2. Розвиток і розширення поняття про число в історичному аспекті та ШКМ
3. Аналіз програми та шкільних підручників про розвиток поняття числа
4. Конспект уроку для 5 класу на тему «Ряд натуральних чисел»
Висновки
Список використаної літератури
Вступ
Актуальність теми. Поняття про число належить до найбільш стародавніх теоретичних розділів математики. Розвиток чисел має величезне значення для багатьох розділів математики. Теорія чисел в сучасному розумінні вивчає не тільки властивості цілих раціональних чисел, але й властивості чисел дійсних або комплексних, причому, для доведення своїх тверджень вона вживає аналітичні засоби, які належать іншим галузям математики, наприклад, математичному аналізу, теорії функцій комплексної змінної, алгебрі тощо. Крім того, в багатьох питаннях про числа мають велике значення геометричні міркування. Використовуючи при розв’язуванні своїх задач, різні математичні дисципліни, теорія чисел відіграє велику роль у розвитку і вдосконаленні цих дисциплін.
Об’єкт дослідження – вивчення поняття розвитку про число в ШКМ.
Предмет дослідження – специфіка розвитку поняття про числа, арифметичні дії з числами, їх властивості та застосування.
Мета дослідження полягає в теоретичному обґрунтуванні всіх числових множин.
Основним завданням дослідження є охарактеризувати методику введення поняття натуральних, цілих, дробових, раціональних, ірраціональних, дійсних, комплексних чисел.
Для розв’язання поставленого завдання застосовувався комплекс методів дослідження: – теоретичні – аналіз науково-методичної літератури з теми дослідження, а також порівняння, систематизація, зіставлення та узагальнення здобутої інформації з метою обґрунтування сутності розвитку поняття про число.
Теоретична значущість роботи полягає у висвітленні сучасними науковцями питань розвитку поняття про число.
1. Історія виникнення чисел та поняття числа
Вчені вважають, що історія виникнення чисел зародилася ще в доісторичні часи, коли людина навчилася рахувати предмети. Але знаки для позначення чисел з'явилися значно пізніше: їх винайшли шумери – народ, який жив у 3000-2000 рр.. до н. е. в Месопотамії (нині в Іраку). Історія свідчить, що на табличках з глини вони видавлювали клиноподібні рисочки, а потім винайшли знаки. Деякі клинописні знаки позначали числа 1, 10, 100, тобто були цифрами, інші числа записувалися за допомогою з'єднання цих знаків. Користування цифрами полегшувало рахунок: рахували дні тижня, голови худоби, розміри земельних ділянок, обсяги врожаю.
Вавилоняни, які прийшли в Месопотамію після шумерів, успадкували багато досягнень шумерської цивілізації – збереглися клинописні таблички з перекладом однієї одиниці вимірювання в інші. Користувалися цифрами і стародавні єгиптяни – про це свідчить математичний папірус Ринда, названий по імені англійського єгиптолога, який придбав його в 1858 р. в єгипетському місті Луксорі. На папірусі записані 84 математичні завдання з рішеннями. Судячи з цього історичного документу, єгиптяни користувалися такою системою цифр, в якій число позначалося сумою значень цифр.
Для позначення деяких чисел (1, 10, 100 і т. д.) виник окремий ієрогліф. При записі якогось числа ці ієрогліфи писали стільки разів, скільки в цьому числі одиниць відповідного розряду. Схожа система числення була у римлян; вона виявилася однією з найбільш довговічних: іноді нею користуються і зараз. У ряду народів (стародавні греки, фінікійці) цифрами служили букви алфавіту.
Історія свідчить про прообрази сучасних арабських цифр, які з'явилися в Індії пізніше V ст. Але індійські цифри в X-XIII ст. потрапили до Європи завдяки арабам, звідси і виникла назва – «арабські». Велика заслуга у поширенні і виникненні індійських цифр в арабському світі належала працям двох математиків: середньоазіатського вченого Хорезмі (бл.780 - бл.850) і араба Кінді (бл.800 – бл.870). Хорезмі, який жив у Багдаді, написав арифметичний трактат про індійські цифри, який став відомий в Європі в перекладі італійського математика Леонардо Пізанського (Фібоначчі).
Текст Фібоначчі зіграв вирішальну роль у тому, що арабо-індійська система запису чисел вкоренилася на Заході. У цій системі значення цифри залежить від її положення в запису (так, в числі 151 цифра 1 ліворуч має значення 100, а праворуч – 1). А арабська назва нуля – Сифре – стало словом «цифра». Широке поширення в Європі арабські цифри отримали з другої половини XV ст.
Поняття числа розвивалося в тісному зв'язку з вивченням величин; цей зв'язок зберігається і тепер. У всіх розділах сучасної математики доводиться розглядати різні величини і користуватися числами.
Існує велика кількість визначень поняття «число».
Перше наукове визначення числа дав Евклід у своїх «Початки», яке він, очевидно, успадкував від свого співвітчизника Евдокса Книдского (близько 408 - близько 355 рр.. до н. е..): «Одиниця є те, відповідно до чого кожна з існуючих речей називається однією. Число є множиною, складеною з одиниць ». Так визначав поняття числа і російський математик Магніцький у своїй «Арифметиці» (1703 р.).
Ще раніше Евкліда Аристотель дав таке визначення: «Число є множиною, яка вимірюється за допомогою одиниць».
Зі слів грецького філософа Ямвліха, ще Фалес Мілетський - родоначальник грецької стихійно-матеріалістичної філософії - вчив, що «число - це система одиниць». Це визначення було відомо і Піфагору.
У своїй «Загальній арифметиці» (1707 р) великий англійський фізик, механік, астроном і математик Ісаак Ньютон пише: «Під числом ми розуміємо не стільки множину одиниць, скільки відношення однієї величини до іншої, взятої за одиницю. Число буває трьох видів: ціле, дробове і ірраціональне. Ціле число є те, що вимірюється одиницею; дробове - кратною частиною одиниці, ірраціональне - число, не сумірне з одиницею».
2. Розвиток і розширення поняття про число в історичному аспекті та ШКМ
Поняття числа, як і поняття множини, належить до числа основних фундаментальних понять сучасної математики. Число є основним знаряддям, за допомогою якого людина пізнає кількісні відношення реального світу. Поняття натурального числа виникло ще на початку розвитку людської цивілізації як відображення найпростіших потреб людської діяльності. Тому є досить природним те, що сучасне вивчення про число базується на арифметиці саме натуральних чисел. Зміст подальшого розгортання цього вчення полягає в тому, що розширення множини натуральних чисел відбувається за наступною схемою:
Вивчення чисел у шкільному курсі математики відбувається у такій послідовності: натуральні числа, нуль, дробові числа (додатні), від’ємні числа і множина раціональних чисел, ірраціональні числа і множина дійсних чисел. Ця послідовність відображає історичний шлях розвитку поняття числа в математиці:
Відмінність між історичною і логічною схемами пояснюється тим, що дробові числа історично з’явилися набагато пізніше від’ємних чисел. Адже ще стародавні грецькі математики використовували дробові додатні числа, у той час як багато математиків XVI ст. ще не визнавали від’ємних чисел. Тому за логічною схемою розвитку після натуральних чисел вивчаються цілі числа. Варто зазначити, що структура множини
Виникає питання: чому не привести у відповідь схему розвитку поняття числа у шкільному курсі з розвитком цього поняття в сучасній науці? Шкільна схема зазвичай обґрунтовується з точки зору педагогічних міркувань, виходячи з того, що поняття дробового числа (додатного) доступніше для розуміння учнями, ніж поняття від’ємного числа. Взагалі, психолого-педагогічні міркування, що стосуються доступності навчального матеріалу є досить вагомою умовою для відхилення від логіки наукової системи у шкільному навчанні.
Побудова розширення числової множини повинна задовольняти наступним чотирьом умовам:
Нова множина чисел повинна містити вже відому множину;
Смисл дій над числами в старій множині залишається тим самим у новій множині;
У новій множині виконується дія, яку не можна було виконати в старій множині;
Нова множина чисел повинна бути такою, щоб не існувало жодної її підмножини, яка містила б попередню множину і задовольняла ті самі умови.
Різні способи побудови
Нехай множина
Важливим моментом процесу розширення поняття про число у шкільному навчанні є розкриття ідеї цього розширення, пояснення основної його мети. Не можна обмежуватися у навчанні лише формальним обґрунтуванням необхідності введення нових чисел для забезпечення виконання операцій.
У шкільному навчанні слід перед введенням нових чисел наводити приклади практичних задач, що не мають розв’язків (не завжди мають розв’язки) на відомій множині чисел. Для того, щоб розв’язати цю задачу, ми і розширюємо відому множину.
3. Аналіз програми та шкільних підручників про розвиток поняття числа
Основні відомості про натуральні числа та дії над ними розглядаються в початкових класах. Передбачається навчити учнів читати, записувати порівнювати числа, виконувати усні та письмові обчислення в межах п’ятицифрових чисел. В п’ятому класі відомості про натуральні числа повторюють, систематизують та поглиблюють. Вперше фактично натуральні числа розширюють до цілих невід’ємних
Далі ідея розширення поняття числа послідовно розвивається в шкільному курсі математики за історичною схемою розвитку цього поняття, а саме:
Тобто, теоретичні принципи розширення поняття числа, що застосовуються в курсі алгебри ВНЗ, порушуються. Адже там числа вводяться за наступною схемою:
За діючою програмою звичайні дроби в шкільному курсі математики вивчають в три етапи:
Пропедевтично в 4 класі вивчають поняття дробу, чисельника, знаменника; навчають порівнювати дроби, знаходити дріб від числа і число за його дробом.
На другому етапі в 5 класі відомості про звичайні дроби повторюють та розширюють, вводять нові поняття правильного та неправильного дробу, цілої та дробової частини числа. Основна мета вивчення звичайних дробів у 5 класі полягає у ознайомленні учнів з початковими відомостями про них у обсязі, достатньому для вивчення десяткових дробів.
На третьому етапі в 6 класі триває вивчення звичайних дробів. Вивчається основна властивість дробу, скорочення, порівняння, додавання і віднімання дробів з різними знаменниками, множення та ділення дробів. Основною метою вивчення дробів у 6 класі є формування стійких навичок перетворення дробів і виконання дій над ними.
Введення дробових чисел є важливим етапом у процесі розширення поняття числа. На кожному етапі розширення виникає потреба навчитися порівнювати нові числа і виконувати дії над ними. При цьому слід означити або пояснити поняття суми, різниці, добутку і частки нових чисел.
Діюча програма передбачає основні відомості про десяткові дроби вивчати в 5 класі. Основною метою вивчення десяткових дробів у 5 класі є формування вміння читати, записувати, порівнювати, округлювати десяткові дроби та виконувати дії над ними. Поняття десяткового дробу вводять або як окремого випадку звичайного дробу, або як поширення позиційного принципу нумерації вправо від одиниці.
Програма та підручник з математики передбачають вивчення додатних і від’ємних чисел після звичайних дробів у 6 класі. Основною метою вивчення цілих чисел є розширення поняття числа за допомогою введення від’ємних чисел, формування навичок порівняння та виконання дій над цими числами.
Після вивчення цілих чисел поняття числа розширюється введенням ірраціональних чисел. Всі відомості про раціональні числа учні отримують у 1-6 класах. Відповідно діючої програми ірраціональні і дійсні числа вивчають у 8 класі без багатьох означень і доведень фактично на інтуїтивному рівні.
Під час вивчення квадратних рівнянь у зв’язку з потребою розв’язання найпростіших рівнянь, наприклад
Натурального числа
Поняття «натуральне число» належить до первісних, неозначуваних понять. У теоретичних курсах зміст його розкривається через систему аксіом, наприклад аксіом Пеано. У теорії множин натуральне число означають як потужність скінченної множини. На жаль, у деяких шкільних підручниках, наприклад у підручнику Нурк Е.Р, Тельгмаа А.Е. під час розгляду цього поняття наведено твердження, які учні, навіть старшокласники, сприймають і фіксують у пам'яті як означення. Зокрема, у ньому сказано: «Числа 1, 2, 3,..., що використовуються під час лічби предметів, називаються натуральними». У цьому твердженні небажано вживати слово «називаються», а доцільніше сказати «дістали назву», оскільки йдеться лише про термін, а не про зміст поняття «натуральне число».
Перш ніж розглядати питання про читання і записування багатоцифрових натуральних чисел, потрібно повторити з учнями поняття про розряди і розрядні одиниці, класи десяткової системи числення, співвідношення між розрядними одиницями, записування числа у вигляді суми розрядних одиниць, домогтися правильного вживання учнями слів «цифра» і «число». Щоб учні розрізняли поняття «цифра», «число» і правильно використовували ці терміни, слід звернути їхню увагу на те, що цифри - це умовні знаки для позначення чисел. Десяткова система числення має тільки десять цифр, за допомогою яких позначається безліч натуральних чисел. У зв'язку з цим є добра нагода на уроці коротко згадати про інші системи числення, зокрема про римську й інші нумерації. На занятті математичного гуртка можна докладніше розповісти про історію виникнення різних систем числення і нумерацій. Вважаємо, що під нумерацією розуміють спосіб читання (усна нумерація) і записування (письмова нумерація) чисел. У цьому разі не можна ототожнювати «нумерацію» з «системою числення». У тій самій системі числення, наприклад десятковій, можуть бути різні нумерації.
Для здійснення перспективних зв'язків з десятковими дробами потрібно повторити основну властивість десяткової системи числення, що виражає співвідношення між розрядними одиницями. Зокрема, слід звернути увагу учнів на основну властивість в іншому формулюванні: одиниця кожного розряду в десять разів менша від одиниці розряду, яка міститься ліворуч, і в десять разів більша за одиницю розряду, що міститься праворуч (крім одиниці розряду одиниць, біля якого поки що немає розрядів праворуч). Достатню увагу потрібно приділити з'ясуванню позиційного принципу десяткової системи числення та її переваг перед непозиційними системами, наприклад римською.
Під час повторення поняття класів доцільно дати учням орієнтир щодо назви класів, оскільки в цьому учні часто припускаються помилок. Назва класу визначається назвою розряду, який містить останню цифру класу. Практика доводить, що стійкі навички читання багатоцифрових чисел в учнів формуються й усвідомлюються швидше, якщо сформулювати їм правило читання багатоцифрових натуральних чисел.
Для того щоб прочитати багатоцифрове натуральне число, потрібно:
1) розбити число на класи справа наліво;
2) якщо найвищий клас містить три цифри, то прочитати зліва направо кожний клас як трицифрове число і додати назву класу; назва останнього класу (класу одиниць) не додається;
3) якщо найвищий клас містить одну або дві цифри, то прочитати його як одноцифрове або двоцифрове число і додати назву цього класу; peштy класів читати так само, як у попередньому випадку.
Під час записування багатоцифрових чисел учні припускаються найбільше помилок у разі відсутності певних розрядів або цілих класів. Пов'язано це з тим, що деякі учні недостатньо усвідомлюють принцип поділу чисел на класи і розряди, погано знають назви класів, починаючи від класу одиниць і до класу мільярдів і, навпаки, починаючи від класу мільярдів до класу одиниць.
Учитель має на конкретних прикладах пояснити спосіб міркувань під час записування таких чисел. Наприклад, нехай потрібно записати число двадцять вісім мільярдів два мільйони сорок три. Міркуємо так: за класом мільярдів міститься клас мільйонів, в якому має бути три цифри, а є лише одна третя цифра (2), отже, ліворуч від неї потрібно поставити два нулі. За класом мільйонів міститься клас тисяч, а в нашому прикладі цього класу немає, тому після цифри 2 ставимо три нулі. У першому класі (класі одиниць) має бути також три цифри, а є тільки дві останні (43), тому ліворуч від цифри 4 ставимо нуль. Дістаємо: 28 002 000 043.
Зробимо кілька зауважень.
1. Кращому засвоєнню десяткової системи числення сприяє використання звичайної рахівниці.
2. У системі вправ досить обмежитись першими чотирма класами, оскільки надалі в інших предметах і в практиці для позначення великих чисел зазвичай користуються степенем числа 10. Щоправда, учням молодших класів цікаві назви інших класів - трильйони, квадрильйони, квінтильйони, секстильйони і т. д. Проте рекомендувати запам'ятати ці назви недоцільно.
3. Повторенню і розширенню десяткової нумерації сприяють вправи, що стосуються метричної системи мір.
4. Реалізації перспективних зв'язків з вивченням комбінаторики сприяють вправи на зразок: скільки трицифрових чисел можна скласти, записавши їх за допомогою лише цифр 2, 3 і 9 за умови, що в запису числа не повинно бути однакових цифр.
Цілого числа
Числова вісь із числовими позначками є універсальною моделлю цілих чисел.
Розглядаючи числову вісь, звертаю увагу учнів, що число 0 – особливе, воно не є додатним і не є від’ємним, тобто 0 відіграє роль «межі» між додатними та від’ємними числами.
Відкладаючи на числовій прямій точки, що відповідають числам, формуємо усвідомлення того, що число має два значення: розташування відносно початку відліку і відстань від точки до початку відліку. Якщо взяти якесь число а, то його знак вказує, де відносно початку відліку знаходиться точка, що відповідає заданому числу а. Звертаю увагу учнів, що відстань від початку відліку до точки, що відповідає заданому числу, називають модулем числа або абсолютною величиною.
Під час вивчення теми «Модуль числа» треба домогтися не формального, а усвідомленого засвоєння цього поняття.
Під час вивчення додавання та віднімання чисел за допомогою числової осі бажано сформувати в учнів розуміння того, що для будь-якого числа, число а+1 більше від а, оскільки розташоване праворуч від а; число а-1 менше від а, оскільки розташоване ліворуч від а. Розуміння цього факту допоможе учням під час розв’язання задач.
Виконання дій над цілими числами на початковому етапі допомагає учням краще засвоїти, зрозуміти та запам’ятати правило додавання додатних і від’ємних чисел. число шкільний математика натуральний
Вдосконалюючи обчислювальні навички учнів з цілими числами, поступово поповнюємо вирази дробовими числами, таким чином знайомимо учнів з раціональними числами.
Дробового числа
Учитель має розуміти принципову відмінність між поняттями «дріб» і «дробове число». Звичайний дріб (так само десятковий дріб, проценти) - це лише форма, символ для запису як дробового, так і цілого числа. Наприклад, дробове число
У 4 класі та в курсі математики 5 - 6 класів дріб трактують спочатку як частину цілого (яблука, круга, відрізка тощо), а пізніше - як частку від ділення двох натуральних чисел. Під час формування поняття звичайного дробу, порівняння дробів з однаковими знаменниками потрібно широко використовувати наочність і практичні вправи на розбивання відрізків, круга, прямокутників та інших об'єктів на рівні частини і позначення за допомогою дробу різних частин цілого, а також пов'язувати вивчення цього матеріалу з метричною системою мір (довжина, площа, об'єм, грошові одиниці, час тощо) і вимірюванням різних величин, що показує учням походження дробів з практичної діяльності людей.
Важливо розглянути зображення дробів на координатному промені та розв'язування оберненої задачі. На координатному промені легко пояснити основну властивість дробу і порівняння дробів.

У зв'язку зі скороченням дробів можна запропонувати рис.2, який не тільки переконає учнів в існуванні різних записів того самого числа, а й дасть змогу усвідомити відмінність між поняттями «дріб» і «дробове число».

В навчальній і методичній літературі відомі два підходи до тлумачення і введення десяткового дробу. В традиційному курсі арифметики десятковий дріб пояснювали як окремий випадок звичайного дробу, а всю теорію десяткових дробів виводили з відповідної теорії звичайних дробів. Другий підхід не використовує тлумачення десяткового дробу як окремого випадку звичайного, а ґрунтується на позиційному принципі десяткової нумерації та ідеї поширення вправо від одиниці основної властивості розрядних одиниць десяткової системи числення (одиниця кожного розряду в десять разів менша за одиницю розряду, що міститься ліворуч, і в десять разів більша за одиницю розряду, що міститься праворуч).
Другий підхід передбачає перед розглядом десяткових дробів проведення уроку на повторення десяткової системи числення та метричної системи мір. При цьому слід наголосити на основній властивості розрядних одиниць десяткової системи саме в формі, наведеній вище, і звернути увагу на аналогічне співвідношення між одиницями метричної системи мір. Зокрема,
Пояснення вчителя під час введення десяткових дробів може бути таким. Невідома учням до цього часу форма запису чисел, наприклад 98,7; 103,6; 8,67, дістала назву «десяткові дроби». Утворення десяткових дробів відбувається за тим самим позиційним принципом десяткової системи числення, що і натуральних чисел. Відомо, що одиниця кожного розряду в натуральному числі крім розряду одиниць містить десять одиниць розряду, що розміщуються праворуч. Інакше кажучи, одиниця кожного такого розряду в десять разів більша за одиницю розряду, що міститься праворуч, і в десять разів менша за одиницю розряду ліворуч, тобто становить десяту його частину.
Раціонального числа
Всі відомості про раціональні числа учні дістають з курсу математики 1-6 класів. Перш ніж вводити поняття ірраціонального числа, потрібно провести бесіду, присвячену ідеї розвитку поняття числа, систематизації й узагальненню відомостей про раціональні числа. Зміст бесіди може бути таким.
У попередніх класах вивчались різні множини чисел. У цьому разі розширення відомої множини чисел виконувалось так, щоб: 1) нова множина чисел містила вже відому множину; 2) смисл дій над числами у відомій множині залишався тим самим у відомій множині; 3) у новій множині виконувалась дія, яку не можна було виконати у відомій множині; 4) нова множина чисел була такою, щоб не існувало жодної її підмножини, яка містила б попередню множину і задовольняла ті самі умови.
Справді, множину Nнатуральних чисел, які першими виникли в практичній діяльності людей, після введення числа 0 і від'ємних чисел, протилежних натуральним, було розширено до множини цілих чисел Z. У множині Z смисл дій над натуральними числами залишається тим самим, але крім додавання і множення стає завжди можливою дія віднімання. Після введення дробових чисел (додатних і від'ємних) множина цілих чисел розширюється до множини раціональних чисел Q. Умножині раціональних чисел стає завжди можливою дія ділення, крім ділення на нуль, а смисл дій, які виконувались у попередніх множинах чисел, залишається тим самим і в цій множині.
Кожне раціональне число можна подати у вигляді дробу (частки)
Кожне раціональне число можна зобразити єдиною відповідною точкою на координатній прямій.
Важливо на конкретних прикладах перетворення звичайних дробів на десяткові переконати учнів, що кожний звичайний дріб можна подати у вигляді десяткового дробу - скінченного чи нескінченного, але обов'язково періодичного. Всі цілі числа та скінченні десяткові дроби можна подати у вигляді нескінченного періодичного десяткового дробу з нулем у періоді. Отже, кожне раціональне число можна подати у вигляді нескінченного періодичного десяткового дробу. На цьому етапі навчання немає потреби ознайомлювати учнів з правилами перетворення періодичних десяткових дробів на звичайні. Слід наголосити: якщо не розглядати періодичні дроби з числом 9 у періоді, то кожному десятковому періодичному дробу відповідатиме єдине раціональне число. У таких випадках кажуть, що відповідність між множиною раціональних чисел і множиною нескінченних періодичних десяткових дробів взаємно однозначна.
Ірраціонального числа
Традиційно введення нових, ірраціональних чисел пов'язують із задачею вимірювання відрізків. У традиційному шкільному курсі математики ірраціональні числа впроваджувались у старших класах. При цьому попередньо запроваджувалось поняття сумірних і несумірних відрізків, доводилось твердження про те, що діагональ квадрата зі стороною, що дорівнює одиниці довжини, несумірна зі стороною. Далі для позначення довжини несумірних відрізків вводились ірраціональні числа, будувалась множина дійсних чисел, розглядались порівняння та дії над числами в цій множині.
За сучасних умов відповідно до чинної програми потрібно вивчати ірраціональні числа і множину дійсних чисел у 8 класі на доступнішому рівні за коротший час, без багатьох означень і доведень або фактично на рівні уявлень. Тому мотивування і введення ірраціональних чисел можна здійснити за таким методичним варіантом.
На одиничному відрізку координатної прямої будують квадрат (рис.3) і ставлять за мету визначити довжину його діагоналі ОК,а відповідне число зобразити точкою Рна координатній прямій. Геометрично це виконати легко відкладанням циркулем відрізка ОКна координатній прямій. Однак виникає запитання: яким числом виражається координата Р? Щоб з'ясувати це, позначимо довжину відрізка ОКбуквою хі побудуємо ще один квадрат, стороною якого є відрізок ОК(рис.4). З рисунка випливає, що площа цього квадрата вдвоє більша за площу одиничного квадрата. Отже, х= 2, оскільки площа одиничного квадрата дорівнює 1.
Щоб визначити х,потрібно розв'язати квадратне рівняння. Графічний спосіб його розв'язування (рис.5) свідчить, що існують два корені цього рівняння. Квадрат кожного з них дорівнює 2. З попереднього навчального матеріалу учні вже знають, що число, квадрат якого дорівнює 2, називають квадратним коренем. Арифметичний квадратний корінь позначається символом V2. Тому два корені рівняння х = 2є не що інше, як числа v2 і -V2. Які це числа?
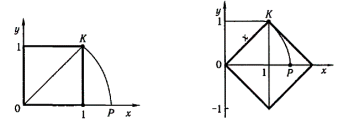
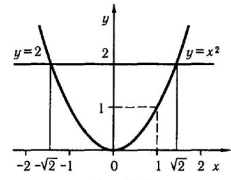
Далі формулюють і доводять методом від супротивного твердження: не існує раціонального числа, квадрат якого дорівнює 2.
Отже, корені
Такі числа називають ірраціональними. Префікс “ir” латинською мовою означає «не». Не слід думати, що ірраціональні числа можна отримати лише добуванням квадратного кореня з деяких раціональних чисел. Ірраціональним є число, що виражає відношення довжини кола до діаметра.
Пізніше учням стане відомо, що ірраціональними числами виражається значення тригонометричних функцій, логарифмів. Число е, що є границею вигляду
 .
.Учитель має зауважити, що можна обчислити з якою завгодно кількістю десяткових знаків наближене значення числа
Подальше обчислення значень
Ірраціональних чисел можна утворити безліч, якщо записувати нескінченні десяткові дроби, наприклад, так: 12,010 010 001... або 8,020 022 000 222... .
Дійсного числа
Якщо множину раціональних чисел доповнити числами ірраціональними, то отримаємо розширену множину, яку називають множиною дійсних чиселі позначають літерою R.У множині дійсних чисел є можливою дія добування коренів з раціональних чисел і деякі інші математичні операції.
Оскільки дійсні числа записують у вигляді нескінченних десяткових дробів (періодичних або неперіодичних), то їх можна порівняти за тими самими правилами, що й десяткові дроби.
Введення ірраціональних чисел показало, що координатна пряма має точки, яким не відповідає жодне раціональне число. Після впровадження ірраціональних чисел і утворення множини Rдійсних чисел виконується взаємно однозначна відповідність між множиною точок координатної прямої та множиною дійсних чисел. Це означає, що кожній точці координатної прямої відповідає дійсне число (її координата) і, навпаки, кожному дійсному числу відповідає точка на координатній прямій.
З теоретичних курсів відомо, що строга теорія дійсних чисел досить складна. Тому учням 8 класу надають лише спрощені відомості про цю множину. Щодо виконання чотирьох арифметичних дій над дійсними числами, то учням досить сказати, що в цій множині виконуються всі арифметичні дії, крім ділення на нуль. Якщо хоча б одне з чисел є ірраціональним, дії виконують над їхніми наближеними значеннями, взявши попередньо ці наближення з однаковою кількістю десяткових знаків. Можна на прикладі проілюструвати учням додавання або віднімання двох ірраціональних чисел. Наприклад,
Якщо потрібно обчислити цю суму точніше, то наближені значення доданків беруть із більшою кількістю десяткових знаків.
Комплексного числа
Програма передбачає вивчення комплексних чисел лише в класах з поглибленим вивченням математики або на факультативних заняттях. Можна розглянути цю тему і на заняттях математичного гуртка.
При першому підході до введення поняття «комплексне число» можна скористатися наступною методикою.
1. Встановлюється взаємно однозначна відповідність між множиною дійсних чисел і множиною точок числової прямої. Стверджується (із залученням теорії геометрії), що існує взаємно однозначна відповідність між парами чисел і точками координатної площини. І як наслідок: кожну пару дійсних чисел, записаних в певному порядку, логічно розглядати як деяке нове число, зображуване деякою точкою координатної площини.
Означення. Пара дійсних чисел
2. Виділяється підмножина
Означення. Комплексне число виду
Комплексне число виду
Для числа виду
Далі визначаються дії на множині комплексних чисел, заданих парами. І тільки потім вводиться уявна одиниця, алгебраїчна та тригонометрична форми запису комплексного числа і правила виконання дій з урахуванням форми запису.
При підході Ш.А. Алімова до введення поняття «комплексного числа» рекомендується наступна методика роботи.
1. Мотиваційний момент: знаходження коренів рівняння
Означення. Комплексними числами називають вирази виду
2. Тут же визначаються супутні поняття: дійсна і уявна частини комплексного числа.
3. Далі вводяться дії з комплексними числами в алгебраїчній формі, дається геометрична інтерпретація комплексного числа, тригонометрична форма запису і дії з комплексними числами в тригонометричній формі запису.
4. Конспект уроку для 5 класу на тему «Ряд натуральних чисел»
Мета: узагальнити і поглибити знання учнів про натуральні числа; формувати вміння розпізнавати натуральні числа, наводити їх приклади.
Тип уроку: засвоєння нових знань.
Хід уроку
I. Організаційний момент
ІІ. Актуалізація опорних знань
Оскільки тема не є новою для п'ятикласників, доцільно провести з учнями бесіду:
- Скільки тобі років?
- Скільки кольорів у веселки?
- Скільки предметів ти будеш вивчати у цьому навчальному році?
Після отримання відповідей учитель нагадує учням, що названі числа мають дещо спільне — використовуються для лічби, тому називаються натуральними числами.
Після цього можна запропонувати учням навести приклади натуральних чисел, що означають кількість учнів у ряду, кількість учнів у класі тощо (при цьому учні повторюють, як записуються і читаються багатоцифрові числа).
Далі вчитель пропонує учням дати відповідь на запитання:
- Яку частину тижня складають робочі дні?
- Яку частину навчального року складає один семестр?
- Яку частину року складає літо?
- Скільки в класі навчається людей, віком старше ніж 20 років?
Кожне з названих чисел учні (або учитель) записують на дошці (і в зошитах), після чого учитель запитує учнів, чи є названі числа натуральними. Після цього учитель ще раз акцентує увагу учнів на тому, що:
1) числа, що використовуються під час лічби предметів, є натуральними;
2) не всі числа, які знаємо, є натуральними.
Тепер учні готові сприймати додаткові знання про властивість натуральних чисел.
IІI. Вивчення нового матеріалу
Цей етап уроку також доцільно провести у вигляді евристичної бесіди. Для здобуття знань про основні властивості натуральних чисел доцільно запропонувати учням, наприклад, такі запитання:
- Якщо треба порахувати кількість учнів у класі (зошитів на парті, поверхів у будинку тощо), то з якого числа починаємо лічбу? Отже, яке натуральне число є найменшим?
- Як відрізняється кожне наступне число від попереднього? А від наступного?
- Яке натуральне число передує числу 365, стоїть за числом 349?
Після відповідей на запитання учитель разом з учнями робить важливі висновки:
1. Найменшим натуральним числом є 1.
2. Найбільшого натурального числа не існує.
3. Усі натуральні числа, записані в порядку зростання, утворюють ряд натуральних чисел.
Наприклад: 1, 2, 3, 4, 5, ... — ряд натуральних чисел; 1, 2, 4, 5 — не є рядом натуральних чисел.
IV. Закріплення нових знань і вмінь учнів
Усні вправи
1. Назвіть 14 перших натуральних чисел (учні з місця називають по черзі по одному числу в прямому і зворотному напрямках).
2. Чи є в ряді натуральних чисел: 1) найменше число; 2) найбільше число?
3. Чи кожне число в ряді натуральних чисел має: 1) наступне число; 2) попереднє число?
4. Чого не вистачає в запису 1, 2, 3, 4, 5, 6, 7, 9, 10, 11, ... щоб він позначав натуральний ряд?
5. Дано натуральний ряд чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ... Скільки натуральних чисел стоїть в ньому між числами 2 і 6; 2 і 9; 2 і 12 (після простого підрахунку запропонувати визначити закономірність: між
Письмове виконання вправ (з коментарем учнів з місця або біля дошки)
№…. (Повторити ще раз висновок, зроблений під час розв'язання усних вправ.)
Додатково
Розгадайте анаграму і знайдіть зайве слово: ОСЛИЧ; ЛЬНУ; РІДБ; НАСІТ.
(Розв'язання. Число; нуль; дріб; стіна; зайве — стіна.)
V. Підсумок уроку
Перед оголошенням домашнього завдання доцільно ще раз повторити з учнями основні поняття, що були розглянуті на уроці.
- Які числа є натуральними?
- Наведіть приклади чисел, що не є натуральними.
- Назвіть найменше натуральне число.
- Чи існує найбільше натуральне число?
- Який запис називається рядом натуральних чисел? Скільки натуральних чисел стоїть у натуральному ряду між 100 і 900?
Висновки
Розвиток поняття числа є важливою наскрізною змістовно-методичною лінією шкільного курсу математики, що проходить в тій чи іншій степені через всі класи середньої школи. Потім ця лінія відображається у вищих учбових закладах у викладанні курсу «Числові системи».
Фундаментальність поняття числа у світі математики потребує вдосконалення методики вивчення числової змістової лінії шкільного курсу, знаходження нових засобів її узагальнення, особливо у школах математичного профілю. Одним із шляхів вдосконалення методики формування вмінь узагальнювати навчальний матеріал, а також: орієнтації на зближення шкільних математичних курсів з сучасною математичною наукою є ознайомлення учнів з основними поняттями сучасної математики які виконують у ній узагальнюючі функції.
До таких понять належать поняття алгебраїчної операції, алгебраїчної структури, математичної моделі. Поняття математичної моделі широко застосовується у різних галузях. Визначальна роль математичного моделювання для сучасної науки висуває відповідні вимоги до математичної підготовки учнів. Доцільно, щоб вони якомога раніше усвідомили ідею математичного моделювання. Математична модель реальної ситуації в багатьох випадках являє собою математичну структуру певного типу. Об’єкти цієї структури трактуються як (ідеалізовані) реальні «речі» (або поняття), а абстрактні відношення між: цими об’єктами – як конкретні зв’язки між елементами дійсності. Отже використання ідеї алгебраїчної структури дозволяє узагальнити знання учнів з числової змістової лінії шкільного курсу, сприяє інтеграції знань учнів у межах курсу алгебри.
Список використаної літератури
Бевз В.Г. Історія математики у фаховій підготовці майбутніх учителів: Монографія. – К.: НПУ імені М.П. Драгоманова, 2005.
Бевз В.Г. Практикум з історії математики: Навч. посіб. для студентів фізико-матем. факультетів пед. університетів. – К.: НПУ імені М.П. Драгоманова, 2004.
Бевз Г.П. Про числа // Математика в школі. - №2. – 2002. – С.6 – 9.
Берман Г.Н. Число и наука о нем. Общедоступные очерки по арифметике натуральных чисел. – М.:Мир, 1960.
Болгарский Б.В. Очерки по истории математики. Изд. 2-е. – Минск: Высшей. школа, 1975.
Бородін О.І. Історія розвитку поняття про число і системи числення. – К.: Рад. школа, 1963.
Гейзер Г.И. История математики в школе. 4-6 кл.: Пос. для учителей. – М.: Просвещение, 1981.
Гейзер Г.И. История математики в школе. 7-8 кл.: Пос. для учителей. – М.: Просвещение, 1982.
Гейзер Г.И. История математики в школе. 9-10 кл.: Пос. для учителей. – М.: Просвещение, 1983.
Груденов Я.И. Психолого-дидактические основы методики обучения математики. – М.: Педагогика, 1987.
Гейзер Г.И. История математики в школе. 4-6 кл.: Пос. для учителей. – М.: Просвещение, 1981.
Бевз Г.П., Бевз В.Г. Математика: Підруч. для 5 кл. загальноосвіт. навч. закл. – К.: Зодіак-ЕКО, 2005. – 352 с.: іл.