Ім'я файлу: 3.3.ru.uk.docx
Розширення: docx
Розмір: 100кб.
Дата: 07.01.2021
скачати
Пов'язані файли:
123.docx
2.3.docx
3.2.docx

Визначимо для різницевих рівнянь (відображень) деякі поняття, аналогічні основним поняттям теорії диференціальних рівнянь.

Рішення (траєкторія) - будь-яка послідовність значень , що задовольняє даному різницевого рівняння при будь-якому t. Різним початкових значень відповідають різні рішення.

Рівновагою називається рішення виду: 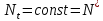, яке задовольняє співвідношенню 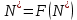. Повертаючись до формули (4.10), видно, що для рівноважного стану .

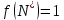Як і в випадку диференціальних рівнянь, для дослідження стійкості застосуємо лінійний аналіз. покладемо

.

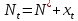Лінеарізуя рівняння (4.8), тобто розкладаючи F в ряд за ступенями 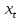і відкидаючи члени порядку 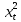і вище, отримуємо

.







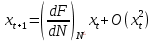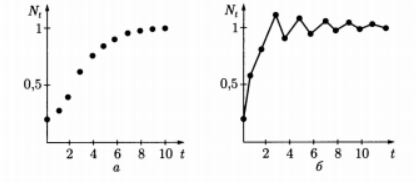
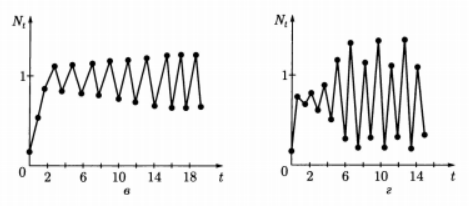
Мал. 4.13. Графіки чисельності популяції, складені за формулою

(4.11):

а - монотонний зростання; б - затухаючі коливання; в - двоточковий цикл; г - чотирьохточковий цикл; д, е приклади хаотичних рішень

З умов збіжності геометричній прогресії слід, що для линеарізованногo рівняння

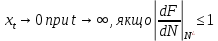(Рівновага стійка),

і

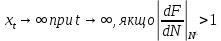(Рівновага нестійка).

Позначимо.

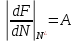
У разі стійкої рівноваги:

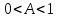• - відхилення від рівноваги зникають ионo- томно;

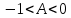• - затухаючі коливання навколо

Графіки монотонного н немонотонного прагнення чисельності до рівноважного стану в моделі (4.11) представлені на рис. 4.13.

У разі нестійкої рівноваги:

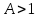• - відхилення від рівноваги монотонно зростає;

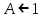• - відхилення від рівноваги у вигляді наростаючих коливань.

При 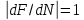геометрична прогресія сходиться, однак для з'ясування характеру збіжності (наявності монотонності) потрібне додаткове дослідження членів вищого порядку.

Для рівняння (4.11) рівновага знаходиться з виразу

.

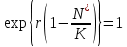Єдине рівноважне значення 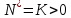існує при будь-якому r. Рівновага стійко, якщо 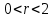, рішення монотонно при 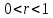і являє собою затухаючі коливання при .
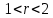скачати

© Усі права захищені
написати до нас