8 клас
Центральні та вписані кути

Означення. Центральним кутом кола називають кут з вершиною в центрі кола.
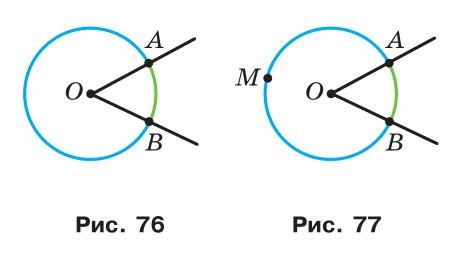
На рис.76 кут AOB — центральний. Сторони цього кута перетинають коло в точках A і B. Ці точки ділять коло на дві дуги, які виділено на рис.76 різним кольором. Точки A і B називають кінцями дуги, вони належать кожній з виділених дуг. Кожну із цих дуг можна позначити так: ∪AB (читають: «дуга AB»).
Дуга AB належить центральному куту AOB (рис. 77). У цьому випадку говорять, що центральний кут AOB спирається на дугу AB.
Кожна дуга кола, як і все коло, має градусну міру. Градусну міру всього кола вважають рівною 360°.
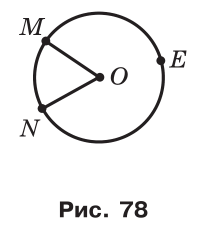
Якщо центральний кут MON спирається на дугу MN (рис.78), то градусну міру дуги MN вважають рівною градусній мірі кута MON і записують: ∪MN = ∠MON (читають: «градусна міра дуги MN дорівнює градусній мірі кута MON»). Градусну міру дуги MEN (рис.78) вважають рівною 360° – ∠MON.
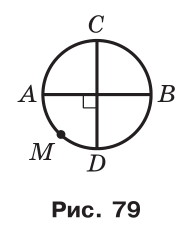
На рис.79 зображено коло, у якому проведено два перпендикулярних діаметри AB і CD. Тоді ∪AMD = 90°, ∪ACD = 360° –– 90° = 270°, ∪ACB = ∪ADB = 180°. Кожну з дуг ACB і ADB називають півколом. На рис.79 півколами є також дуги CAD і CBD.
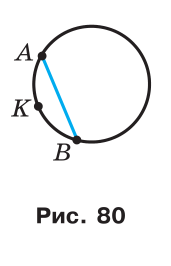
Про хорду, яка сполучає кінці дуги, говорять, що хорда стягує дугу. На рис.80 хорда AB стягує кожну з дуг AB і AKB.
Будь-яка хорда стягує дві дуги, сума градусних мір яких дорівнює 360°.

Означення. Вписаним кутом кола називають кут, вершина якого належить колу, а сторони перетинають коло.
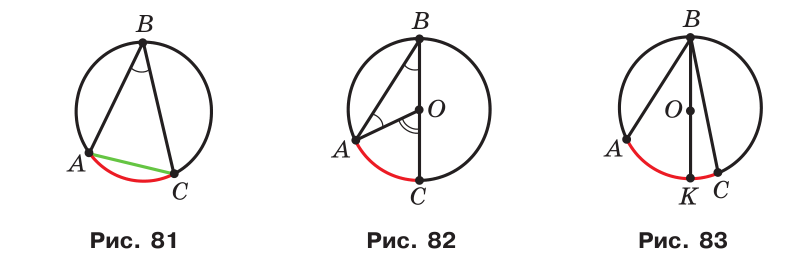
На рис.81 кут ABC — вписаний. Дуга AC належить цьому куту, а дуга ABC — не належить. У такому випадку говорять, що вписаний кут ABC спирається на дугу AC. Також можна сказати, що вписаний кут ABC спирається на хорду AC.

Теорема 9.1. Градусна міра вписаного кута дорівнює половині градусної міри дуги, на яку він спирається.
Існує три випадки розташування центра O кола відносно вписаного кута ABC:
Випадок 1. Центр O належить одній зі сторін кута, наприклад, стороні BC (рис. 82).
Випадок 2. Центр O належить куту, проте не належить жодній із його сторін (рис. 83).
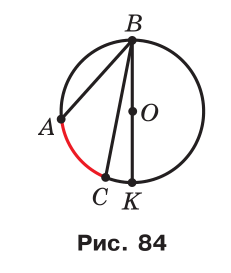
Випадок 3. Центр O не належить куту (рис. 84).

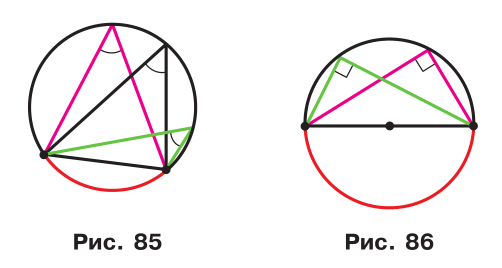
Наслідок 1. Вписані кути, які спираються на одну й ту саму дугу, рівні (рис. 85).
Наслідок 2. Вписаний кут, який спирається на діаметр (півколо), — прямий (рис. 86).