19. В партии из 300 деталей 200 деталей I сорта, 60 деталей II сорта, остальные III сорта. Какова вероятность того, что три наугад отобранные детали будут одного сорта.
Решение
Пусть событие
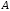состоит в том, что три наугад отобранные детали будут одного сорта. Введем дополнительные события. Пусть событие 
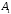состоит в том, что выбранная деталь первого сорта, событие 
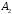состоит в том, что выбранная деталь окажется второго сорта и 
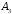соответственно третьего сорта. Общее количество деталей третьего сорта 
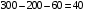. Вычислим вероятности событий 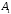, , 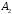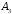с помощью классического определения вероятности 
, 
, 
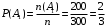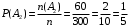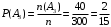
Запишем введенное событие
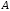через события 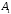, , 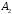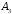. Т.е.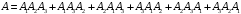
Теперь запишем на основании полученного выражения и теорем сложения и умножения вероятности вероятность события
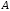
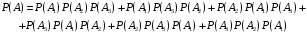
Теперь подставим числовые значения в выражение, записанное выше:
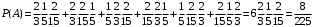
Ответ:
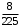
22. Производятся испытания прибора. При каждом испытании прибор выходит из строя с вероятностью р. После первого выхода из строя прибор ремонтируется; после второго признается негодным. Найти вероятность того, что прибор окончательно выйдет из строя в точности при k-том испытании.
Решение
Поскольку по условию прибор испытывается до второй поломки, то очевидно, что при последнем (
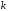-том) испытании прибор второй раз вышел из строя. Значит, до этого последнего испытания прибор ровно 1 раз выходил из строя, т.е. было 
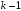испытания (не считая последнего). Воспользуемся формулой Бернулли.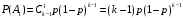
Вероятность события
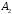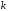– при -м испытании прибор второй раз вышел из строя, равна: 
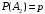. По формуле умножения вероятностей, вероятность события 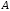− прибор будет признан негодным после 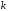испытаний, равна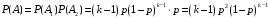
Ответ:
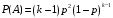
26. Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле.
Решение
Путь вероятность того при четырех выстрела было хотя бы одно попадание
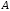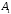, - событие попадания в цель при одиночном выстреле. Введем событие 
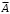противоположное событию 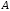которое состоит в том, что не было ни одного попадания по мишени. Иначе об этом можно было сказать так: по мишени не попали при первом выстреле и при втором, и при третьем и четвертом. На языке событий можно записать это так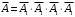
Таким образом вероятность противоположного события равна
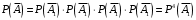
где
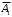- событие промаха при одиночном выстреле. Несложно догадаться что события 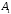и 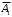формируют полную группу событий. Следовательно 
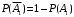. Так же события 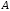и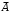 
также образуют полную группу событий для которых можно записать аналогичное соотношение 
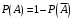, выражение для 
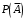таким образом выражение для 
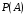можно записать следующим образом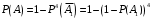 
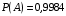, дано по условию. Если положить искомую величину 
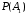через 
, то получим следующее уравнение решая которое мы ответим на вопрос поставленный в задаче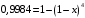 
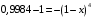
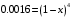
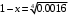
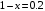
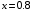
Следовательно
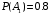
Ответ:
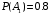
28. Для одной торпеды вероятность потопить корабль равна 0,5. Какова вероятность того, что 4 торпеды потопят корабль, если для потопления корабля достаточно одного попадания торпеды в цель
Решение
Пусть событие
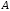состоит в том, что 4 торпеды потопят корабль, тогда событие 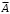состоит в том, что 4 торпеды не потопят корабль. Введем событие 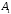которое состоит в том, что одиночная торпеда потопит корабль, тогда 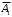состоит в том, одиночная торпеда не потопит корабль. События 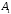и 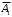образуют полную группу событий. По условию задачи 
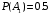, следовательно 
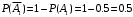. Событие 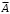можно представить в терминах события 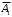, т.е. 
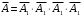, а соответствующие вероятность события 
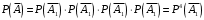, подставляя числовые значения получим 
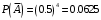. Значит вероятность искомого события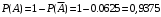 
Ответ:
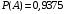
33. В ящике 10 красных и 6 синих пуговиц. Вынимаются наудачу две пуговицы. Какова вероятность того, что пуговицы будут одноцветными?
Решение
Вероятность того что первая пуговица будет красного цвета
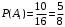(общее число исходов 10+6=16, число исходов благоприятствующих данному событию 10), вероятность того что и вторая пуговица красного при условии что первая красная 
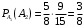(условная вероятность наступления события 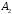вторая пуговица красная при условии выполнения события 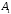) Теперь рассмотрим другую ситуацию. Вероятность того что первая - синяя 
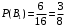(общее число исходов 10+6=16, число исходов благоприятствующих данному событию 6), вероятность того что первая-синяя и вторая тоже синяя 
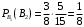. Следовательно искомая вероятность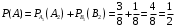 
Ответ:
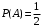
35. Студент пришел на зачет, зная из 30 вопросов только 24. Какова вероятность сдать зачет, если после отказа отвечать на вопрос преподаватель задает еще один вопрос?
Решение
Введем следующие события:
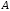- зачет сдан, следовательно 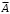- студент не ответил и на 1-ый, и на 2-ой вопросы. 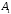- студент не ответил на 1-ый вопрос, 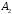- студент не ответил на 2-й вопрос. События 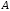и 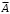образуют полную группу событий, значит можно записать так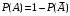
Так как событие
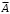состоит в том, что студент не ответил на первый и второй вопрос, то на языке событий этот факт можно записать так 
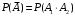, так события 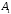и 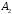зависимы, следовательно произведение этих событий можно записать следующим образом 
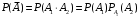. Вероятность наступления события 
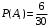(Общее число исходов 30 – всего вопросов которые вынесены на зачет. Так как данное событие состоит в том, что студент не ответит на первый вопрос, следовательно, количество невыученных вопросов 30-24=6), вероятность события 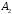при условии, что событие 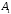уже произошло 
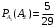(Так как событие 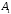уже произошло, в этом случае число благоприятных исходов уменьшается на 1 и общее число исходов так же уменьшается на 1). Следовательно, искомая вероятность 
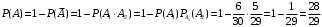.Ответ:
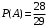
36. В урне два белых и три черных шара. Два игрока поочередно вынимают из урны по шару, не вкладывая их обратно. Выигрывает тот, кто раньше получит белый шар. Найти вероятность того, что выиграет первый игрок.
Решение
Первый игрок выигрывает только в 2-х случаях:
Он сразу вынимает белый шар
Первый игрок вынимает черный шар и второй игрок выбирает черный шар, а потом первый игрок вынимает белый шар
На языке классического определения вероятности первую ситуацию можно записать так
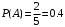(всего шаров 5 два белых)Второй случай несколько сложнее:
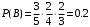(первый множитель, указывает на вероятность того, что первый шар вытащили черным, после наступления этого события черных шаров стало на один шар меньше и следовательно общее число исходов уменьшилось на один. Второй сомножитель указывает вероятность того что второй шар также черный. Т.е. общее число исходов 4 и черных шаров стало 4. Ну и третий сомножитель указывает, что третий шар белый)Так как события
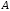и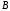 
несовместные, следовательно искомая вероятность выражается следующим соотношением.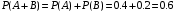 
Ответ: 0,6
39. Имеются две урны: в первой 3 белых шара и два черных; во второй 4 белых и 4 черных. Из первой урны во вторую перекладывают, не глядя, два шара. После этого из второй урны берут один шар. Найти вероятность того, что этот шар будет белым.
Решение
49. Имеется две партии однородных изделий; первая партия состоит из 150 изделий, среди которых 8 дефектных; вторая партия из 75 изделий, среди которых 3 дефектных. Из первой партии берется случайным образом 50 изделий, а из второй 30 изделий; эти 80 изделий смешиваются и образуется новая партия. Из новой смешанной партии берется наугад одно изделие. Найти вероятность того, что изделие будет дефектным.
50. Сообщение состоит из «точек» и «тире». Помехи искажают 2/5 «точек» и 1/3 «тире» (при искажении каждый сигнал переходит в противоположный). В сооб- щении «точки» и «тире» встречаются в отношении 5:3. Определить вероятность того, что принят передаваемый сигнал, если принята а) «точка», б) «тире».
56. Дискретная случайная величина принимает три возможных значения. Найти
, 
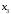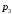, зная, что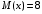 
| | 4 | 6 | |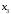
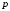 | 0,5 | 0,3 | |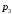
Решение
Вероятности
, 
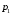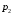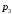, подчиняются следующему условию нормировки
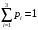или в развернутом виде 
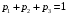, так как значения вероятностей 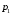, 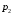нам даны по условию следовательно наше условие перепишется следующим образом. 
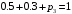, следовательно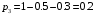 
По определению математическое ожидание применительно к нашему примеру можно записать следующим образом
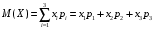
Если подставить числовые значения где это возможно, то получим
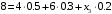
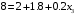
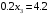
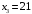
Ответ:
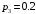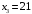
, Вариант 9
1. В ящике имеется 10 перенумерованных однотипных изделий с номерами 1, 2, 3, …, 10. Из ящика 5 раз вынимается наугад по одному изделию, его номер записывается и изделие кладется обратно в ящик. Найти вероятность того, что все записанные номера будут различными.
Решение
Задача на классическое определение вероятности. По определению вероятностью события
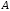которое состоит в том, что все записанные номера будут различные определяется следующим выражением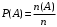 
где
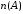- число исходов удовлетворяющих событию 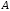, а 
- общее число исходов. Найдем общее число исходов. ПДоставая первое изделие, вероятность того, что он будет новый – 100%=1, доставая второе – 90%=0,9 и т.д. и просто их перемножаем так как нам нужно, чтобы все были под разными номерами 1·0,9·0,8·0,7·0,6=0,3024
2. Внутри круга радиуса R наудачу брошена точка. Найти вероятность того, что точка окажется внутри вписанного в круг правильного шестиугольника.
3. По каналу связи передаются последовательно три сообщения, причем первое из них может быть искажено с вероятностью 0,06; второе – с вероятностью 0,1; третье – с вероятностью 0,02. Определить вероятность того, что не более одного сообщения передано правильно.