Ім'я файлу: Рекурсія - укр.doc
Розширення: doc
Розмір: 544кб.
Дата: 04.03.2020
скачати
Пов'язані файли:
МОДЕЛІ ДАНИХ.ppt
Розширення: doc
Розмір: 544кб.
Дата: 04.03.2020
скачати
Пов'язані файли:
МОДЕЛІ ДАНИХ.ppt
Рекурсією називається ситуація, коли підпрограма викликає сама себе.
1.Сутність рекурсії
Процедура або функція може містити виклик інших процедур або функцій. У тому числі процедура може викликати саму себе. Ніякого парадоксу тут немає - комп'ютер лише послідовно виконує команди, що зустрілися йому в програмі і, якщо зустрічається виклик процедури, просто починає виконувати цю процедуру. Немає ніякої різниці, яка процедура дала команду це робити.
Приклад рекурсивної процедури:
procedure Rec (a: integer);
begin
if a> 0 then
Rec (a-1);
writeln (a);
end;
Розглянемо, що станеться, якщо в основній програмі поставити виклик, наприклад, виду Rec (3). Нижче представлена блок-схема, що показує послідовність виконання операторів.
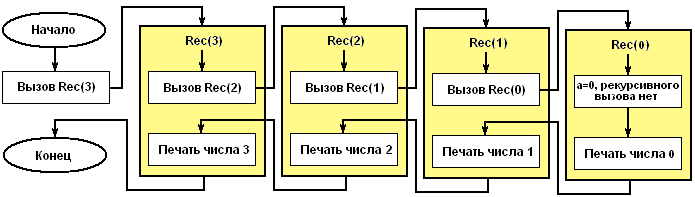
Рис. 1. Блок схема роботи рекурсивної процедури.
Процедура Rec викликається з параметром a=3. У ній міститься виклик процедури Rec з параметром a=2. Попередній виклик ще не завершився, тому можете уявити собі, що створюється ще одна процедура і до закінчення її роботи перша свою роботу не закінчує. Процес виклику закінчується, коли параметр a=0. У цей момент одночасно виконуються 4 примірники процедури.
Кількість одночасно виконуваних процедур називають глибиною рекурсії.
Четверта викликана процедура (Rec(0)) надрукує число 0 і закінчить свою роботу. Після цього управління повертається до процедури, яка її викликала (Rec(1)) і друкується число 1. І так далі поки не завершаться всі процедури. Результатом вихідного виклику буде друк чотирьох чисел: 0, 1, 2, 3.
Ще один візуальний образ того, що відбувається представлений на Рис. 2.
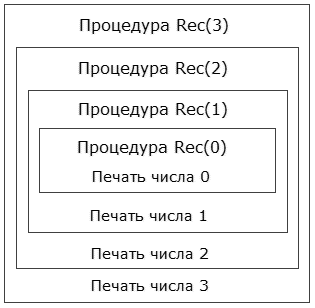
Рис. 2. N-S діаграма роботи рекурсивної процедури.
Виконання процедури Rec з параметром 3 складається з виконання процедури Rec з параметром 2 і друку числа 3. У свою чергу виконання процедури Rec з параметром 2 складається з виконання процедури Rec з параметром 1 і друку числа 2. І т. Д.
Питання.
1. Що вийде при виклику Rec(4).
2. Що вийде при виклику описаної нижче процедури Rec2(4), де оператори помінялися місцями.
procedure Rec2 (a: integer);
begin
writeln (a);
if a> 0 then
Rec2 (a-1);
end;
Примітка . У наведених прикладах рекурсивний виклик розташовується усередині умовного оператора. Це необхідна умова для того, щоб рекурсія коли-небудь закінчилася. Також зверніть увагу, що сама себе процедура викликає з іншим параметром, не таким, з яким була викликана вона сама. Це необхідно, щоб рекурсія не продовжувалась до нескінченності.
Звичайну рекурсію можна уподібнити Уроборосу (Рис. 3).
Рис. 3. Уроборос - змій, який пожирає свій хвіст.
Малюнок з алхімічного трактату «Synosius» Теодора Пелеканоса (1478 р.).
2.Складна рекурсія
Розглянемо більш складну схему: функція A викликає функцію B, а та в свою чергу викликає A. Це називається складною рекурсією.
Приклад:
procedure A (n: integer); {Випереджаючий опис (заголовок) першої процедури}
procedure B (n: integer); {Випереджаючий опис другої процедури}
procedure A (n: integer); {Повний опис процедури A}
begin
writeln (n);
B (n-1);
end;
procedure B (n: integer); {Повний опис процедури B}
begin
writeln (n);
if n <10 then
A (n+2);
end;
Образ складної рекурсії можна почерпнути з відомого дитячого віршика, де «Вовки з переляку, з'їли один одного».
Рис. 4. Складна рекурсія.
3. Імітація роботи циклу з допомогою рекурсії
Якщо процедура викликає сама себе, то, по суті, це призводить до повторного виконання інструкцій, які містяться в ній, що аналогічно роботі циклу. Деякі мови програмування не містять циклічних конструкцій зовсім, надаючи програмістам організовувати повторення за допомогою рекурсії (наприклад, Пролог, де рекурсія - основний прийом програмування).
Для прикладу зімітуєм роботу циклу for. Для цього нам буде потрібна змінна лічильник кроків, яку можна реалізувати, наприклад, як параметр процедури.
Приклад 1.
procedure LoopImitation (i, n: integer);
{Перший параметр - лічильник кроків, другий параметр - загальна кількість кроків}
begin
writeln ( 'Hello N', i); //Тут будь-які інструкції, які будуть повторюватись
if i
LoopImitation (i+1, n); // максимальному значенню n,
//повторюємо інструкції шляхом виклику
//нового екземпляра процедури
end;
Результатом виклику виду LoopImitation (1, 10) стане десятикратне виконання інструкцій зі зміною лічильника від 1 до 10. У даному випадку буде надруковано:
Hello N 1
Hello N 2
...
Hello N 10
Взагалі, не важко бачити, що параметри процедури це межі зміни значень лічильника.
Можна поміняти місцями рекурсивний виклик і інструкції, які підлягають повторенню, як в наступному прикладі.
Приклад 2.
procedure LoopImitation2 (i, n: integer);
begin
if i
LoopImitation2 (i+1, n);
writeln ( 'Hello N', i);
end;
В цьому випадку, перш ніж почнуть виконуватися інструкції, відбудеться рекурсивний виклик процедури. Новий екземпляр процедури також, перш за все, викличе ще один екземпляр і так далі, поки не дійдемо до максимального значення лічильника. Тільки після цього остання з викликаних процедур виконає свої інструкції, потім виконає свої інструкції передостання і т.д. Результатом виклику LoopImitation2 (1, 10) буде друк привітань в зворотному порядку:
Hello N 10
...
Hello N 1
Якщо уявити собі ланцюжок з рекурсивно викликаних процедур, то в Прикладі 1 ми проходимо її від раніше викликаних процедур до пізніших. У Прикладі 2 навпаки від більш пізніх до ранніх.
Нарешті, рекурсивний виклик можна розташувати між двома блоками інструкцій. наприклад:
procedure LoopImitation3 (i, n: integer);
begin
writeln ( 'Hello N', i); {Тут може розташовуватися перший блок інструкцій}
if i
LoopImitation3 (i+1, n);
writeln ( 'Hello N', i); {Тут може розташовуватися другий блок інструкцій}
end;
Тут спочатку послідовно виконуватися інструкції з першого блоку потім в зворотному порядку інструкції другого блоку. При виклику LoopImitation3 (1, 10) отримаємо:
Hello N 1
...
Hello N 10
Hello N 10
...
Hello N 1
Буде потрібно відразу два цикли, щоб зробити те ж саме без рекурсії.
Тим, що виконання частин однієї і тієї ж процедури рознесено по часу можна скористатися при вирішенні різних задач.
Приклад 3: Переклад числа в двійкову систему.
Отримання цифр двійкового числа, як відомо, відбувається за допомогою ділення із залишком на основу системи числення 2. Якщо є число x, то його остання цифра в його дdsqrjdjve поданні дорівнює
.Взявши ж цілу частину від ділення на 2:
,отримаємо число, що має те ж двійкове подання, але без останньої цифри. Таким чином, досить повторювати наведені дві операції поки після чергового поділу не отримаємо цілу частину, рівну 0. Без рекурсії це буде виглядати так:
while x>0 do
begin
c: = x mod 2;
x: = x div 2;
write (c);
end;
Проблема тут в тому, що цифри двійкового представлення обчислюються в зворотному порядку (спочатку останні). Щоб надрукувати число в нормальному вигляді доведеться запам'ятати всі цифри в елементах масиву і виводити в окремому циклі.
За допомогою рекурсії неважко домогтися виведення в правильному порядку без масиву і другого циклу. А саме:
procedure Binar yRepresentation (x: integer);
var
c, x: integer;
begin
{Перший блок. Виконується в порядку виклику процедур}
c: = x mod 2;
x: = x div 2;
{Рекурсивний виклик}
if x> 0 then
BinaryRepresentation (x);
{Другий блок. Виконується в зворотному порядку}
write (c);
end;
Взагалі кажучи, ніякого виграшу ми не отримали. Цифри двійкового представлення зберігаються в локальних змінних, які свої для кожного працюючого примірника рекурсивної процедури. Тобто, пам'ять заощадити не вдалося. Навіть навпаки, витрачаємо зайву пам'ять на зберігання багатьох локальних змінних x. Однак, таке рішення здається красивим.
4. Рекурентні співвідношення. Рекурсія і ітерація
Кажуть, що послідовність векторів
задана рекурентним співвідношенням, якщо заданий початковий вектор 
і функціональна залежність наступного вектора від попереднього 
Простим прикладом величини, що обчислюється за допомогою рекурентних співвідношень, є факторіал
Черговий факторіал
можна обчислити за попереднім як: 
Ввівши позначення
, отримаємо співвідношення: 
Вектора
з формули (1) можна інтерпретувати як набори значень змінних. Тоді обчислення необхідного елемента послідовності полягатиме в періодичному оновленні їх значень. Зокрема для факторіала: x: = 1;
for i: = 2 to n do
x: = x*i;
writeln (x);
Кожне таке оновлення (x: = x*i) називається ітерацією, а процес повторення ітерацій - ітеріруванням.
Звернемо, проте, увагу, що співвідношення (1) є чисто рекурсивним визначенням послідовності та обчислення n-го елемента є насправді багаторазове взяття функції f від самої себе:
Зокрема для факторіала можна написати:
function Factorial (n: integer): integer;
begin
if n>1 then
Factorial:=n*Factorial(n-1)
else
Factorial:=1;
end;
Слід розуміти, що виклик функцій тягне за собою деякі додаткові накладні витрати, тому перший варіант обчислення факторіала буде трохи більш швидким. Взагалі ітераційні рішення працюють швидше рекурсивних.
Перш ніж переходити до ситуацій, коли рекурсія корисна, звернемо увагу ще на один приклад, де її використовувати не слід.
Розглянемо окремий випадок рекурентних співвідношень, коли наступне значення в послідовності залежить не від одного, а відразу від кількох попередніх значень. Прикладом може служити відома послідовність Фібоначчі, в якій кожен наступний елемент є сумою двох попередніх:
При «лобовому» підході можна написати:
function Fib (n: integer): integer;
begin
if n>1 then
Fib: = Fib(n-1) + Fib(n-2)
else
Fib: = 1;
end;
Кожен виклик Fib створює відразу дві копії себе, кожна з копій - ще дві і т.д. Кількість операцій зростає з номером n експоненційно, хоча при ітераційному вирішенні досить лінійної по n кількості операцій.
Насправді, наведений приклад вчить нас не КОЛИ рекурсію не слід використовувати, а тому ЯК її не слід використовувати. Зрештою, якщо існує швидке ітераційне (на базі циклів) рішення, то той же цикл можна реалізувати за допомогою рекурсивної процедури або функції. наприклад:
// x1, x2 - початкові умови (1, 1)
// n - номер необхідного числа Фібоначчі
function Fib (x1, x2, n: integer): integer;
var
x3: integer;
begin
if n>1 then
begin
x3: = x2+x1;
x1: = x2;
x2: = x3;
Fib: = Fib(x1, x2, n-1);
end else
Fib: = x2;
end;
І все ж ітераційні рішення кращі. Питається, коли ж в такому випадку, слід користуватися рекурсією?
Будь-які рекурсивні процедури і функції, що містять всього один рекурсивний виклик самих себе, легко замінюються ітераційними циклами. Щоб отримати щось, що не має простого нерекурсивного аналога, слід звернутися до процедур і функцій, що викликають себе два і більше разів. У цьому випадку множина процедур, що викликаються, утворює вже не ланцюжок, як на Рис. 1, а ціле дерево. Існують широкі класи задач, коли обчислювальний процес повинен бути організований саме таким чином. Якраз для них рекурсія буде найбільш простим і природним способом вирішення.
5. Дерева
Теоретичною базою для рекурсивних функцій, що викликають себе більш ніж один раз, служить розділ дискретної математики, що вивчає дерева.
5.1. Основні визначення. Способи зображення дерев
Визначення: Деревом будемо називати кінцеве безліч T , що складається з одного або більше вузлів, таких що: а) Є один спеціальний вузол, званий коренем даного дерева. б) Решта вузли (виключаючи корінь) містяться в попарно непересічних подмножествах , кожне з яких в свою чергу є деревом. Дерева називаються піддерев даного дерева.
Це визначення є рекурсивним. Якщо коротко, то дерево це безліч, що складається з кореня і приєднаних до нього піддерев, які теж є деревами. Дерево визначається через саме себе. Однак дане визначення осмислено, так як рекурсія конечна. Кожне поддерево містить менше вузлів, ніж її утримує дерево. Зрештою, ми приходимо до піддерев, що містить всього один вузол, а це вже зрозуміло, що таке.
Рис. 3. Дерево.
На рис. 3 показано дерево з сімома вузлами. Хоча звичайні дерева ростуть знизу вгору, малювати їх прийнято навпаки. При малюванні схеми від руки такий спосіб, очевидно, зручніше. Через цю неузгодженість іноді виникає плутанина, коли говорять про те, що один з вузлів знаходиться над або під іншим. З цієї причини зручніше користуватися термінологією, що вживається при описі генеалогічних дерев, називаючи ближчі до кореню вузли предками, а більш далекі нащадками.
Вузли, що не містять піддерев, називаються кінцевими вузлами або листям . Безліч не перетинаються дерев називається лісом . Наприклад, ліс утворюють піддерева, що виходять з одного вузла.
Графічно дерево можна зобразити і деякими іншими способами. Деякі з них представлені на рис. 4. Відповідно до визначення дерево являє собою систему вкладених множин, де ці безлічі або не перетинаються або повністю утримуються одне в іншому. Такі безлічі можна зобразити як області на площині (рис. 4а). На рис. 4б вкладені безлічі розташовуються не на площині, а витягнуті в одну лінію. Рис. 4б також можна розглядати як схему деякої алгебраїчної формули, що містить вкладені дужки. Рис. 4в дає ще один популярний спосіб зображення деревовидної структури в вигляді уступчатого списку.
Рис. 4. Інші способи зображення деревовидних структур: (а) вкладені безлічі; (Б) вкладені дужки; (В) уступчастий список.
Уступчастий список має очевидну подібність зі способом форматування програмного коду. Дійсно, програма, написана в рамках парадигми структурного програмування, може бути представлена як дерево, що складається з вкладених один в одного конструкцій.
Також можна провести аналогію між уступчатим списком і зовнішнім виглядом змістів в книгах, де розділи містять підрозділи, ті в свою чергу поподраздели і т.д. Традиційний спосіб нумерації таких розділів (розділ 1, підрозділи 1.1 і 1.2, подподраздел 1.1.2 і т.п.) називається десятковою системою Дьюї. У застосуванні до дерева на рис. 3 і 4 ця система дасть:
1. A; 1.1 B; 1.2 C; 1.2.1 D; 1.2.2 E; 1.2.3 F; 1.2.3.1 G;
5.2. Проходження дерев
У всіх алгоритмах, пов'язаних з деревоподібними структурами незмінно зустрічається одна і та ж ідея, а саме ідея проходження або обходу дерева . Це - такий спосіб відвідування вузлів дерева, при якому кожен вузол проходиться точно один раз. При цьому виходить лінійна розстановка вузлів дерева. Зокрема існує три способи: можна проходити вузли в прямому, зворотному і кінцевому порядку.
1 2 3 4