Ім'я файлу: 00124709-202a2eac.doc
Розширення: doc
Розмір: 150кб.
Дата: 07.04.2022
скачати
Пов'язані файли:
берестечко курсова.doc
Баев А.А., Левина В.С. - Блокчейн-технология в бухгалтерском уче
Баев А.А., Левина В.С. - Блокчейн-технология в бухгалтерском уче
Методы получения тонких пленок.doc
лаб 1.docx

Разложение в степенной ряд бинома Ньютона.


Одной из самых фундаментальных алгебраических функций, порождающих ряды, является бином Ньютона, выражение которого записывается в виде: (1)

В этом выражении коэффициенты при представляют собой число сочетаний из элементов по и называются биномиальными коэффициентами . Таблица биномиальных коэффициентов для целых значений и в пределах имеет вид:

Табл.1

Таблица биномиальных коэффициентов


0
1
2
3
4
5
6
7
8
9
10

1
1
1



























2
1
2
1
























3
1
3
3
1





















4
1
4
6
4
1


















5
1
5
10
10
5
1















6
1
6
15
20
15
6
1












7
1
7
21
35
35
21
7
1









8
1
8
28
56
70
56
28
8
1






9
1
9
36
84
126
126
84
36
9
1



10
1
10
45
120
210
252
210
120
45
10
1



Биномы целых положительных степеней


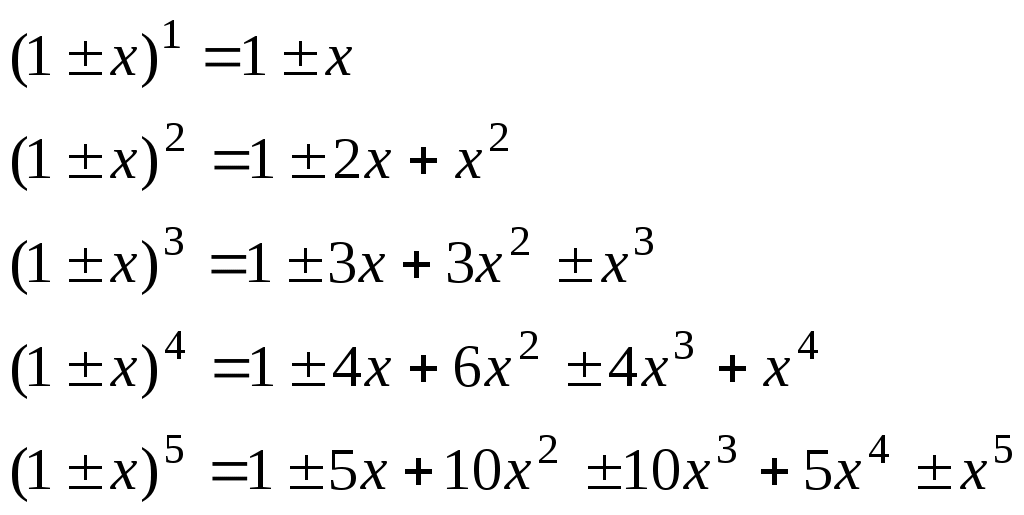
Если показатель степени является целым положительным числом, то выражение бинома состоит из конечного числа слагаемых равного ( ). К примеру,


Эти формулы широко применяются в элементарной математике. Для заданных конечных значений числа эти формулы всегда дают однозначный ответ в форме конечного числа. Биномы целых положительных степеней были известны очень давно, и Ньютон не сказал бы ничего нового в этом отношении, если бы он не совершил исключительно оригинальный по тем временам шаг. Этот шаг состоял в переходе от целых значений числа в биномах к дробным и отрицательным значениям. Хотя правомерность такого перехода не была обоснована строго математически, она дала большой толчок развитию теории числовых и функциональных рядов. Спустя 150 лет Н. Абель доказал правомерность такого перехода строго математически.

Биномы целых отрицательных степеней

Биномы целых отрицательных степеней при помощи формулы (1) записываются в форме бесконечного ряда. К примеру,



(2)





Отметим в качестве указания на фундаментальность формулы бинома Ньютона, что бесконечная геометрическая прогрессия является его частным случаем (см. 1-ю формулу в выражениях (2)).

Любую из этих формул можно получить и без использования формул комбинаторики при помощи элементарной операции деления. Так, например, получается бином минус второй степени:



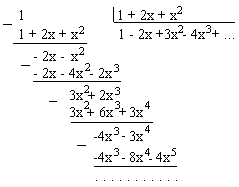
Точно так же можно получить ряд для бинома любой целой отрицательной степени. Все эти биномы имеют радиус сходимости R=1. За пределами этого интервала ряд не воспроизводит значение функции, из которой он получен. Биномы дробных положительных и отрицательных степеней

Биномы дробных положительных и отрицательных степеней раскладываются в ряд при помощи формулы (1), полагая в ней число равным дробному показателю степени бинома. В качестве примера можно представить следующие разложения:





(3)







Ограничения по использованию этих формул показывают, что при положительном показателе степени они применимы в интервале сходимости .

При отрицательных показателях степени они применимы в интервале сходимости <1.

Таким образом, разложения биномов дробных и отрицательных степеней так же характеризуются радиусом сходимости и за пределами этого радиуса не воспроизводят исходную функцию, хотя она существует за этими пределами вплоть до и до .

Все эти ряды можно тождественно преобразовать к виду, который обеспечивает сходимость за пределами интервала ( , +1) в пределах от –1 до и от +1 до . Такое тождественное преобразование выглядит следующим образом: (4)

В преобразованном выражении 4 в скобках заключён тоже бином Ньютона, но уже в другой записи. Раскладывая новый бином в ряд, получим:

(5)

Бесконечный ряд в квадратных скобках последнего выражения сходится в пределах >1, а при n<0 он сходится в пределах . На основании формулы 5 все выше приведённые разложения бинома Ньютона могут быть тождественно преобразованы к виду:

(6)



Суть произведённых преобразований бинома Ньютона к ряду, сходящемуся в бесконечных пределах хорошо видна из последних формул 6. В квадратных скобках каждого разложения стоит ряд абсолютно того же содержания, что и соответствующий ряд в выражениях 4 за исключением того, что вместо аргумента (как было в выражениях 4) в выражениях 6 стоит обратная ему величина , что и делает последний ряд сходящимся. Перед квадратными скобками каждого ряда в выражениях 6 стоит множитель вида , который можно условно назвать масштабирующим множителем. Этот масштабирующий множитель как бы компенсирует влияние перехода в квадратных скобках от аргумента к его обратной величине.

В обобщённой форме эти действия можно записать как преобразование вида: . Такая запись ориентирует на преобразование исходной функции к произведению двух функций и . Последняя функция и позволяет путём разложения перейти к сходящемуся ряду-эквиваленту.

Биномы дробных положительных и отрицательных степеней воспроизводятся только в категориях комбинаторики (выражение 1). Никакие элементарные математические операции не позволяют непосредственным образом получить разложение в ряд бинома дробной степени, как это было в случае биномов целых отрицательных степеней.

Биномы и их разложения в ряд играют в математике исключительно важную роль, поскольку интегрирование этих функций и их разложений в ряд ведёт к алгебраическим, логарифмическим, обратным тригонометрическим и обратные гиперболическим функциям и их разложениям в ряд.

Литература:

1.Е.Е. Алексеева, Е.М. Лушников. Проблемы и решения в теории рядов. Калининград. Изд.„Янтарный сказ”. 2004. 256c.

2 Е.А. Власова. Ряды. Выпуск 9 М.: Изд. МГТУ им. Н.Э. Баумана, 2002. 612с.

3. Н.Н. Воробьёв, Теория рядов. 6-е издание, стереотипное. СПб.: Издательство «Лань», 2002. 408с.
скачати

© Усі права захищені
написати до нас