
Ім'я файлу: 5-Спец-задание-2.doc
Розширення: doc
Розмір: 278кб.
Дата: 15.12.2020
скачати
Пов'язані файли:
Фрагмент з !ДР=Гидравл расч пром песчаной пробки=!ДР.pdf
Розширення: doc
Розмір: 278кб.
Дата: 15.12.2020
скачати
Пов'язані файли:
Фрагмент з !ДР=Гидравл расч пром песчаной пробки=!ДР.pdf
5 Специальное задание на тему:
«распределение давления газожидкостной смеси в вертикальной колонне труб»
5.1 Течение газожидкостного потока в вертикальных колоннах труб
В данном разделе рассмотрены проблемы, возникающие при течении газожидкостной смеси (ГЖС) в скважинах, добывающих газированную жидкость.
Для полного описания газожидкостных смесей указания основных физических свойств любой среды — плотность, вязкость, сжимаемость, теплоемкость, теплопроводность и т.д. — явно недостаточно. Это связано с тем, что ГЖС, состоящая из несмешивающихся фаз, характеризуется целым рядом новых параметров, основными из которых являются: газовое число (газосодержание), относительная скорость, дисперсность, поверхностное натяжение на поверхности раздела фаз, прочность этой поверхности устойчивость ГЖС и др.
Физическую модель, описывающую двухфазный поток в скважинах, можно представить следующими предположениями:
на величину удельного объема текущей смеси существенно влияют изменение температуры и давления от забоя до устья скважины;
кроме потерь на трение о стенки вертикальной колонны труб
при движении газожидкостной смеси происходят потери за счет скольжения фаз относительно друг друга;
жидкость и газ образуют различные структуры потока.
В литературе [3, 4, 9] принята следующая структура двухфазного потока.
1. Пенная или пузырьковая структура.
При таком режиме течения в непрерывной жидкой фазе происходит турбулентное движение мелких газовых пузырьков. Газовый фактор для пенной структуры обычно меньше, чем для других.
2. Пробковая структура.
Газовый фактор в этом случае выше, чем при пенной структуре, и в некоторых местах газ полностью заполняет сечение трубопровода. Пробковая структура – последовательно движущиеся пробки газа и жидкости.
3. Распыленный (дисперсный «туманный») поток.
При таком режиме непрерывной фазой является газовая, в которой распылены мельчайшие частицы жидкой фазы; для такого режима течения характерен еще более высокий газовый фактор
5.2. Классификация методов расчета распределения давления в
вертикальных трубах
5.1.1. Модель гомогенного течения [4, 9].
В данной модели газожидкостная смесь рассматривается в виде однородной гомогенной системы, а процесс ее движения описывается основными законами гидродинамики однофазных сред. При этом предполагается, что жидкая и газовая фазы движутся с одинаковыми скоростями, равными приведенной скорости движения смеси и соответствует пузырьковой структуре потока:
где Vж, Vг – соответственно скорости движения жидкой и газовой фаз, м/с;
Vсм – скорость движения газожидкостной смеси, м/с;
Плотность газожидкостной смеси см рассчитывается с использованием объемного расходного газосодержания г.:
где ж, г – соответственно плотности жидкой и газовой фаз при соответствующих термобарических условиях (Р и Т), кг/м3.
Модель стационарного гомогенного течения описывается двумя уравнениями:
уравнением сохранения массы (уравнением неразрывности)
где Gм – массовый расход смеси, кг/с; f – площадь сечения трубы, м2
уравнением движения
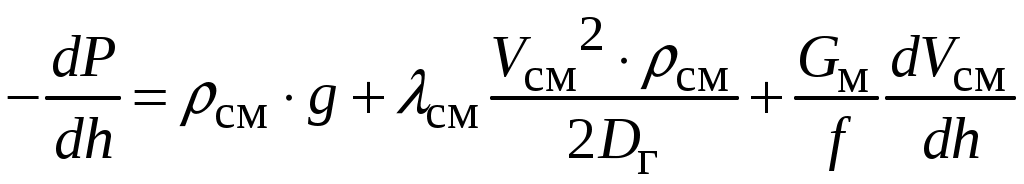 , (5.4)
, (5.4)где см – коэффициент гидравлического сопротивления смеси; Dг – гидравлический диаметр канала, м.
В общем случае баланс давлений для реальной скважины длиной Н можно записать в следующем виде:
Р = Ргс + Ртр + Рин ,
где Р – общий перепад давлений на длине Н, Н/м2; Ргс – потери давления на преодоление веса гидростатического столба ГЖС высотой Н с учетом скольжения газовой фазы, Н/м2; Ртр, Рин – соответственно потери на преодоление трения, инерционные потери (потерями на местных сопротивлениях пренебрегают), Н/м2.
Интегрирование уравнения (5.4) позволяет получить распределение давления как в НКТ, так и в самой скважине.
5.1.2. Модель раздельного течения фаз
Эта модель является более сложной, но более реально отражающей процесс движения ГЖС. Процессы переноса во времени – массы, количества движения (импульса силы) и энергии рассматриваются отдельно для каждой из фаз, а взаимодействие между фазами учитывается условиями протекания этих процессов на границе раздела фаз и на стенках канала.
Все методы расчета ГЖС в подъемниках основаны на результатах лабораторных или промысловых исследований движения в вертикальных трубах. Наиболее полная информация по этим методикам представлена в работах [1, 3, 4, 9].
Перечислим методы, наиболее часто используемые в практике проектирования эксплуатации скважин:
метод Крылова А.П. (структура потока пробковая);
метод Пирвердяна (для обводненных газлифтных скважин);
метод Поэтмана и Карпентера (рекомендуется для расчета общих потерь давления независимо от структуры потока; рекомендуемый диапазон значений дебита 3200м3/сут; газового фактора 18180 м3/м3).
5.3. Метод Ф. Поэтмана и П. Карпентера.
В дипломной работе рассмотрен наиболее простой метод расчета распределения давления при движении ГЖС в вертикальных трубах – метод Ф. Поэтмана и П. Карпентера [1, 3]. Этот метод описывает пузырьковую структуру потока.
Поэтман и Карпентер, основываясь на уравнение Бернулли и пренебрегая изменением кинетической энергии потока, рассматривают движение газожидкостной смеси как течение однородной среды. Основное расчетное уравнение, имеет вид:
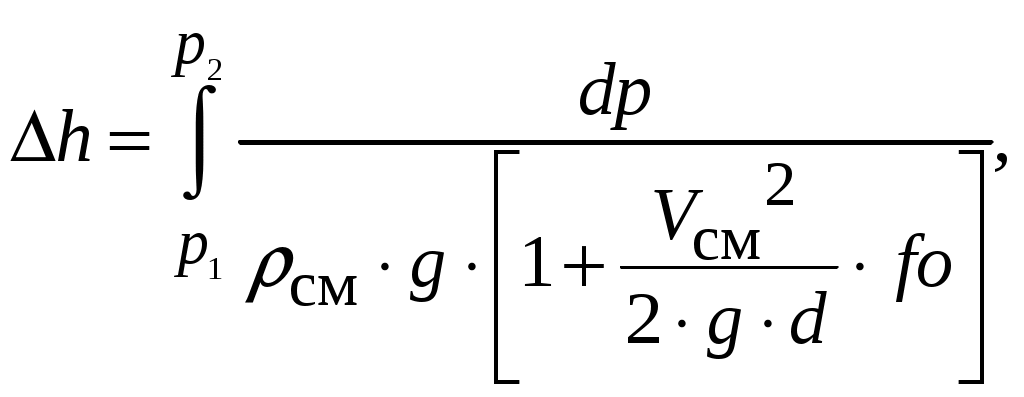 (5.5)
(5.5)где h – расстояние между двумя сечениями трубы, м; р1, р2 – давление в верхнем и нижнем сечениях трубы, Па; ρсм – плотность смеси, кг/м3; Vcм – скорость смеси, м/с; d– диаметр трубы, м; fo – коэффициент гидравлических сопротивлений (учитывает силы трения и скольжение фаз).
Величину h определяют путем численного интегрирования.
Среднюю скорость на участке h определяют по формуле:
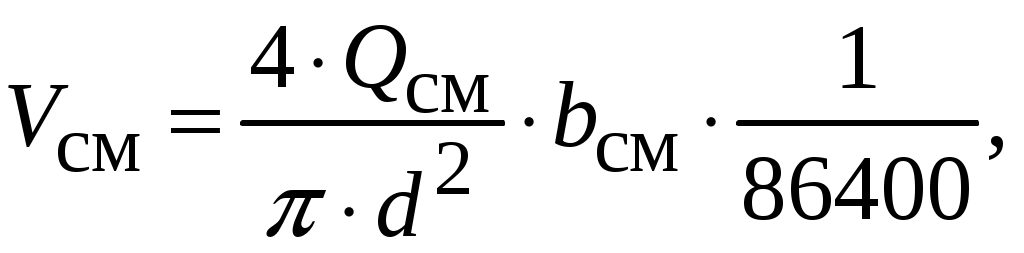 (5.6)
(5.6)где Qсм – расход газожидкостной смеси, м3/сут.
Расчет плотности газожидкостной смеси см ведется по формуле:
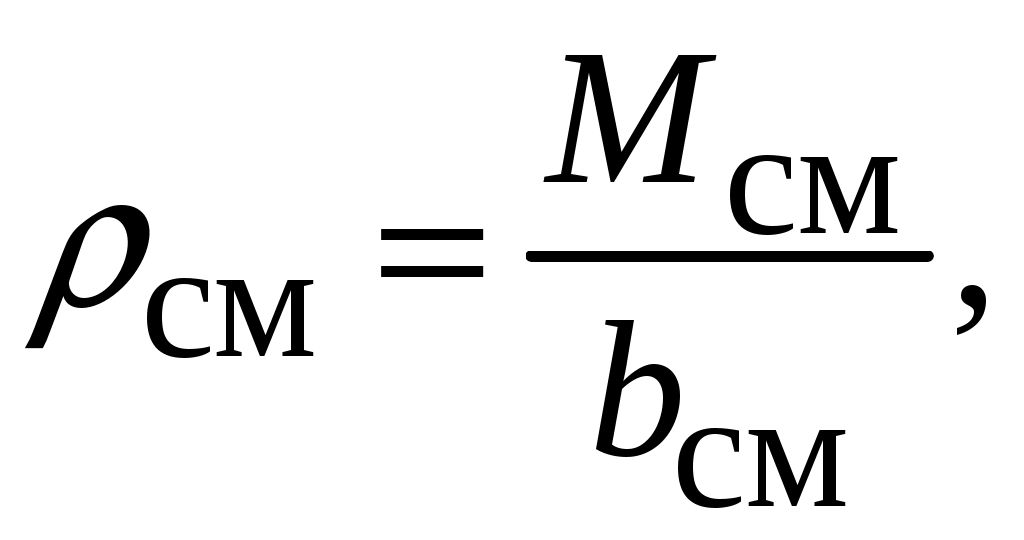 (5.7)
(5.7)где Мсм – массовый фактор газожидкостной смеси, кг/м3; bсм – объемный коэффициент смеси, м3 .
Определим массовый фактор смеси(постоянная величина) по формуле:
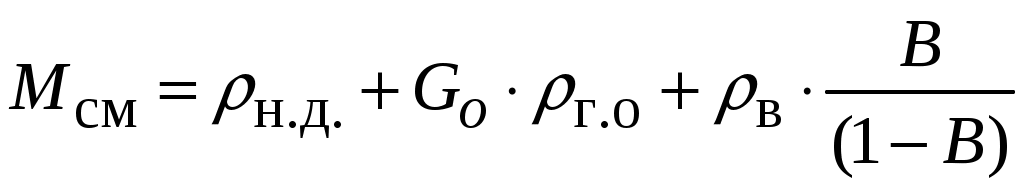 , (5.8)
, (5.8)где
Определим объемный коэффициент смеси:
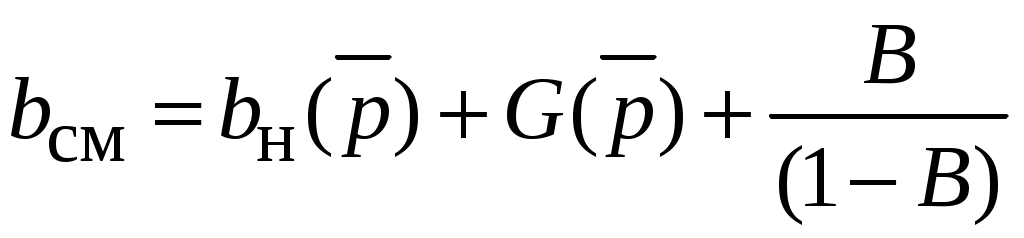 , (5.9)
, (5.9)где
В результате обработки промысловых данных Поэтманом и Карпентером получена графическая зависимость для определения коэффициента сопротивления fo как функции произведения
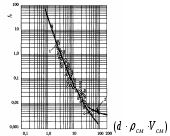
Рисунок 5.1. – График для определения коэффициента сопротивлений fo [4]:
1 – для труб круглого сечения; 2 – для кольцевого пространства
Рассматриваемое произведение
5.4. Численная реализация метода
Исходные данные:
рз – давление на забое, рз=11 МПа и 8 МПа на глубине 1600м;
ру – давление на устье скважины, ру=1,5 МПа
рнас – давление насыщения, рнас=9МПа,
Обводненность – В=0.
Расчетная область скважины разделена на 2 области:
1-я область. При р > рнас – жидкость принимается однофазной, т.к. весь газ полностью растворен в нефти.
2-я область. При ру < р < рнас – из нефти начинает выделяться газ. Газожидкостная смесь становится двух фазной: газ в свободном состоянии и нефть (с растворенным газом или без газа).
На рис. 5.1 представлены результаты расчета методики Поэтмана и Карпентера, реализованной на ЭВМ.
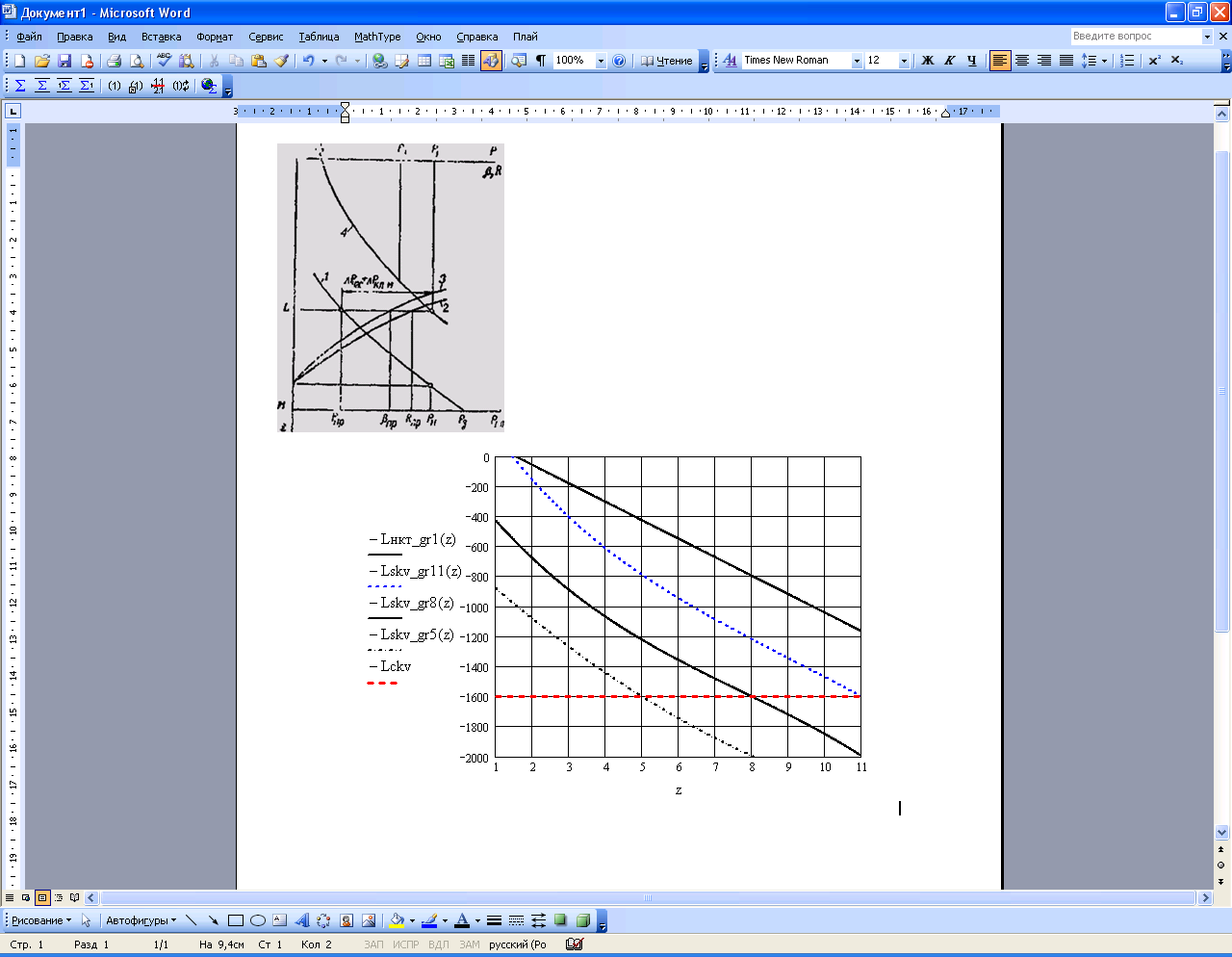
Рисунок 5.1. – Распределение давления вдоль скважины и НКТ
5.5. Учет изменения температуры флюида вдоль скважины
Изначально в методе Поэтмана и Карпентера предполагалось течение изотермическим (Т = соnst), поэтому реализованная на ЭВМ методика расчета распределения давления в вертикальной колонне труб может быть уточнена, если учесть уравнение теплопроводности и линейное изменение температуры от давления.
Расчетная эмпирическая формула для определения температуры флюида вдоль вертикальной колонны труб (обсадные трубы или НКТ) представлена в работе [9, с. 316] и имеет вид:
в зоне НКТ:
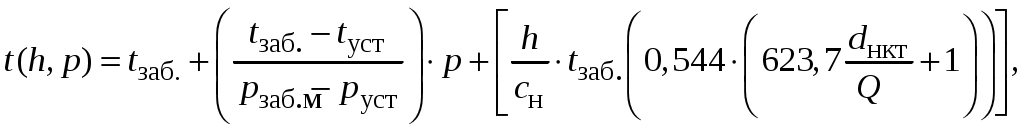 (5.10)
(5.10)в зоне обсадных труб:
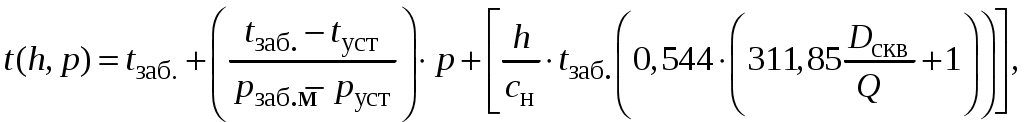 (5.11)
(5.11)где Qм – массовый расход, т/сут; сн – удельная теплопроводность флюида, сн=2100Дж/кгград;
Уточненные значения температуры вдоль скважины (вместо Т=const) подставляются в уравнение состояния реального газа для пересчета количества газа в смеси от давления и температуры:
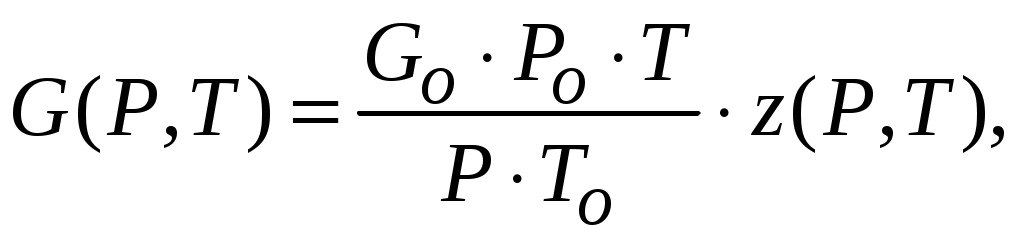
Результаты расчета распределения давления вдоль скважины в дипломной работе используются в главе 2 для выбора оптимальной глубины установки скважинного насоса, а также являются исходными данными для расчета скважинного насоса (расчет расхода газожидкостной смеси, коэффициента сепарации газа на приеме насоса и коэффициента наполнения).