
СПОСОБЫ ОЦЕНКИ ЭФФЕКТИВНОСТИ ЭКОНОМИЧЕСКОГО РЕШЕНИЯ.
КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ. ПОНЯТИЕ ИНФОРМАЦИОННОЙ МОДЕЛИ ОБЪЕКТА.
ПОНЯТИЕ ИМИТАЦИИ. ТРЕБОВАНИЯ К МОДЕЛИ ДЛЯ ИМИТАЦИОННОГО АНАЛИЗА.
ОСОБЕННОСТИ ИМИТАЦИИ КАК МЕТОДА МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ.
ВОЗМОЖНОСТИ ИМИТАЦИИ.
ПОНЯТИЕ МАШИННОГО ИМИТАЦИОННОГО ЭКСПЕРИМЕНТА.
Машинный имитационный эксперимент - метод изучения сложных систем посредством исследования на ЭВМ их математических моделей (совокупности уравнений, описывающих исследуемую систему); имитируя различные условия функционирования системы (путем изменения значений переменных в уравнениях), определяют (по реакции модели) величины, характеризующие поведение системы, ее параметры.
ФОРМУЛИРОВКА ПРОБЛЕМЫ. ВОПРОСЫ, ГИПОТЕЗЫ, ВОЗДЕЙСТВИЯ.
Формулировка проблемы - здесь проводится описание исследуемой проблемы и определение целей исследования; постановка задачи, формулировка и установление иерархии целей и подзадач; изучение поведения системы в целом. Результатом этого этапа должно быть документированное содержательное описание объекта моделирования. Иначе говоря, построение полной информационной модели объекта или системы.
Вопрос – это форма мышления, которая выражает частичное знание о том, что неизвестно для спрашивающего полностью, и которая предполагает устранение этой неизвестности посредством получения дополнительной информации.
Гипотеза – предположение, еще не доказанное логически и не подтвержденное опытом догадки. В результате исследования гипотеза подтверждается или опровергается. В случае своего подтверждения она становится теорией, а если ее опровергнуть, то гипотеза превращается в ложное предположение.
Управляющее воздействие – это информация, которую получает объект управления с помощью своих органов чувств или сигнала от управляющего объекта.
ФОРМУЛИРОВКА МАТЕМАТИЧЕСКОЙ МОДЕЛИ. ОЦЕНКА АДЕКВАТНОСТИ МОДЕЛИ.
Математическая модель (ММ) – это приближенное описание какого-либо класса явлений или объектов реального мира на языке математики.
Адекватность ММ - это соответствие результатов вычислительного эксперимента (ВЭ) поведению реального объекта. Для проверки адекватности ММ служит контрольный ВЭ, воспроизводящий реальный известный случай поведения оригинала в конкретных условиях.
ТИПОВЫЕ МАТЕМАТИЧЕСКИЕ СХЕМЫ ДЛЯ МОДЕЛИРУЮЩЕГО АЛГОРИТМА.
1) непрерывно-детерминированные D‑схемы. Эти схемы применяются для описания различных моделей в теории управления. Математической моделью является задача Коши для обыкновенного дифференциального уравнения или системы обыкновенных дифференциальных уравнений, а также уравнений в частных производных с различными начальными и краевыми условиями. В моделях оптимального управления и некоторых других моделях оптимизации решения находятся при ограничениях на функции, которые имеют линейный, нелинейный или дифференциальный характер;
2) дискретно-детерминированные F‑схемы (конечные автоматы). С помощью этих схем описываются модели устройств контроля и управления, имеющие дискретный характер работы во времени. Математическая модель состоит из задания начального состояния автомата и из уравнений, задающих значения выходных параметров в данный момент времени в зависимости от значений входных параметров и внутренних состояний в данный или предшествующий моменты. Вместо уравнений могут быть использованы таблицы или графы;
3) стохастические модели. В стохастических моделях все или часть переменных множеств Х, Y, Н являются случайными величинами. Это модели регрессионного типа, имеющие большое значение при статистическом анализе наблюдений и непрерывно-стохастические модели (Q‑схемы), которые применяются для описания систем массового обслуживания.
СПОСОБЫ ПОСТРОЕНИЯ МОДЕЛИРУЮЩИХ АЛГОРИТМОВ (УПРАВЛЕНИЕ ВРЕМЕНЕМ).
В настоящий момент известны четыре основных принципа регламентации событий:
Принцип Δt («дельта-тэ»). Принцип состоит в том, что алгоритмом моделирования имитируется движение, то есть изменение состояния системы, в фиксированные моменты времени
Принцип особых состояний. Особые состояния — это такие состояния в изолированные моменты времени, в которых характеристики системы изменяются скачкообразно.
Принцип последовательной проводки заявок. Принцип состоит в том, что каждая заявка отслеживается от момента поступления ее в систему до момента ее выхода из системы. И только потом рассматривается следующая заявка.
Принцип параллельной работы объектов (объектный принцип моделирования). Такой подход моделирования отдельных объектов независимо друг от друга позволяет собирать сколь угодно сложные системы без изменения их составляющих. Принцип объектного моделирования обеспечивает модернизацию сложных систем, удлиняя жизненный цикл АСУ.
ПОНЯТИЕ МЕТОДА МОНТЕ-КАРЛО. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА ПО МЕТОДУ МОНТЕ-КАРЛО.
Метод Монте-Карло лежит в основе статистического моделирования, заключающегося в том, что модель испытывается множеством случайных сигналов с заданной плотностью вероятности с целью получения выходных результатов
Геометрический алгоритм Монте-Карло интегрирования:
Сгенерируем в квадрате kw случайных точек. Пусть kr – количество точек, которые попали вовнутрь рассматриваемой фигуры. При больших значениях kw площадь фигуры R может быть оценена как:
S = kr / kw.
Для общего случая, нетрудно видеть, что исходными данными являются: сторона a квадрата, который содержит фигуру R, и количество точек kw, которые случайным образом выбираются внутри квадрата. Если известно число kr тех случайно выбранных точек, которые размещены в фигуре R, то площадь фигуры можно вычислить по формуле:
S = (kr / kw) * a^2.
Обычный алгоритм Монте-Карло интегрирования:
Рассмотрим случайную величину u, равномерно распределённую на отрезке интегрирования [a, b]. Тогда
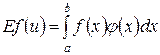 ,
,где
Таким образом, искомый интеграл выражается как:
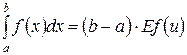 .
.Но математическое ожидание случайной величины
Итак, бросаем на [a, b] N равномерно распределённых точек, и для каждой точки
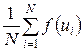 .
.В итоге получаем оценку интеграла:
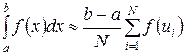 .
.Точность оценки зависит только от количества точек
МОДЕЛИРОВАНИЕ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ.
Для решения задач методом Монте-Карло необходимо получать на ЭВМ последовательность выборочных значений случайной величины с заданным распределением. Такой процесс принято называть моделированием случайной величины.
Для того чтобы смоделировать (разыграть) дискретную случайную величину Х, заданную определенным законом распределения:
| Х | X1 | Xn |
| p | p1 | pn |
надо:
разбить интервал (0,1) на n частичных интервалов:
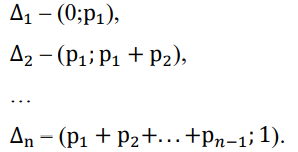
выбрать случайное число rj.
Если случайное число rj попало в частичный интервал
МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ СОБЫТИЙ. МОДЕЛИРОВАНИЕ ПОЛНОЙ ГРУППЫ СОБЫТИЙ.
Моделирование случайного события заключается в воспроизведении факта появления или не появления случайного события в соответствии с заданной его вероятностью. Моделирование полной группы несовместных событий A1, A2. .... Аn, вероятности которых P(Ai) = Рi; i = 1, n известны, можно свести к моделированию дискретной случайной величины Y, имеющей закон распределения:

При практической реализации данного способа на единичном отрезке числовой оси откладывают интервалы.
МЕТОД ОБРАТНОЙ ФУНКЦИИ. МОДЕЛИРОВАНИЕ РАВНОМЕРНОГО РАСПРЕДЕЛЕНИЯ.
МЕТОД ОБРАТНОЙ ФУНКЦИИ. МОДЕЛИРОВАНИЕ ПОКАЗАТЕЛЬНОГО РАСПРЕДЕЛЕНИЯ
МЕТОД СВЕРТОК. МОДЕЛИРОВАНИЕ РАСПРЕДЕЛЕНИЯ ЭРЛАНГА
МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН С НОРМАЛЬНЫМ ЗАКОНОМ РАСПРЕДЕЛЕНИЯ
МЕТОД ОТБОРА. МОДЕЛИРОВАНИЕ УСЕЧЕННОГО НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ
МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ВЕЛИЧИН С ПРОИЗВОЛЬНЫМ РАСПРЕДЕЛЕНИЕМ
ПОНЯТИЕ ПОКАЗАТЕЛЯ ЭФФЕКТИВНОСТИ. ВИДЫ ПОКАЗАТЕЛЕЙ ЭФФЕКТИВНОСТИ
ПОНЯТИЕ КРИТЕРИЯ ЭФФЕКТИВНОСТИ. ВИДЫ КРИТЕРИЕВ ЭФФЕКТИВНОСТИ
ОЦЕНКА ПРИГОДНОСТИ МОДЕЛИ
ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
СВОЙСТВА ЧИСЛЕННЫХ МОДЕЛЕЙ
КЛАССИФИКАЦИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ЭКОНОМИЧЕСКИХ СИСТЕМ
МОДЕЛИ МАССОВОГО ОБСЛУЖИВАНИЯ. ВИДЫ СМО
ОДНОКАНАЛЬНАЯ ОДНОФАЗОВАЯ ИМИТАЦИОННАЯ МОДЕЛЬ МАССОВОГО ОБСЛУЖИВАНИЯ
МОДЕЛИ УПРАВЛЕНИЯ ЗАПАСАМИ
МОДЕЛИ ТОРГОВЛИ. МОДЕЛЬ КОМПАНИИ ПИЛЛСБЕРИ
МОДЕЛЬ ТОРГОВЛИ КОМПАНИИ АНХОЙЗЕР-БУШ
ФИНАНСОВЫЕ МОДЕЛИ. МОДЕЛЬ ГЕРЦА
ПАУТИНООБРАЗНЫЕ МОДЕЛИ ВЗАИМОДЕЙСТВИЯ ФИРМЫ И РЫНКА. МОДЕЛЬ 1
ПАУТИНООБРАЗНЫЕ МОДЕЛИ ВЗАИМОДЕЙСТВИЯ ФИРМЫ И РЫНКА. МОДЕЛЬ 2
ПАУТИНООБРАЗНЫЕ МОДЕЛИ ВЗАИМОДЕЙСТВИЯ ФИРМЫ И РЫНКА. МОДЕЛЬ 3
МОДЕЛЬ КОНКУРЕНТНОЙ ОТРАСЛИ
МОДЕЛЬ ДУОПОЛИИ И ОЛИГОПОЛИИ