| Основи Дискретної Математики :: Теорія кодування | |
Розділ VIІ. Теорія кодування
Питання кодування здавна відігравало значну роль у математиці. Наприклад, десяткова позиційна система числення – це спосіб кодування натуральних чисел. Римські цифри – інший спосіб кодування натуральних чисел, до того ж більш наглядний та природній: палець – І, п’ятірня – V, дві п’ятірні – Х. Але при цьому способі кодування складніше виконувати арифметичні дії над великими числами, тому він був витиснений позиційною десятковою системою.
Раніше засоби кодування відігравали допоміжну роль і не розглядались як окремий предмет математичного вивчення, але з появою комп’ютерів ситуація радикально змінилась. Теорія кодування виникла у 40-х роках XX століття після появи робіт К. Шенона. У цій теорії досліджуються методи кодування, пов’язані з основними математичними моделями, які відображають істотні риси реальних інформаційних систем.
Кодування буквально пронизує інформаційні технології і є центральним питанням при розв’язанні самих різних (практично усіх задач) програмування:
представлення даних довільної природи (наприклад, чисел, тексту, графіки) у пам’яті комп’ютера;
захист інформації від несанкціонованого доступу;
забезпечення перешкодозахищеності при передачі даних по каналам зв’язку;
стиснення інформації у базах даних.
Властивості, які вимагаються від кодування, бувають різної природи:
існування декодування – це дуже природна властивість, але навіть вона потрібна не завжди. Наприклад, трансляція програми на мові високого рівня у машинні команди – це кодування, для якого не потрібно однозначного декодування;
перешкодозахищеність, або виправлення помилок – коли від кодування вимагається можливість відновлення інформації в разі її пошкодження;
задана складність (або простота) кодування та декодування. Наприклад, у криптографії вивчаються такі способи кодування, при яких є просто обчислювальна функція F, але визначення зворотної функції F-1 потребує дуже складних обчислень.
В цьому розділі буде розглянуто деякі найбільш важливі задачі теорії кодування та продемонстровано застосування більшої частини згаданих тут методів.
Лекція 31. Теорія кодування
31.1. Алфавітне й рівномірне кодування
Без утрати загальності можна сформулювати задачу кодування так.
Означення 31.1. Нехай задано алфавіт А = {a1,…,an} зі скінченної кількості символів, які називають буквами. Скінченну послідовність букв алфавіту А називають словом у цьому алфавіті. Для позначення слів будемо використовувати малі грецькі літери: = ai1ai2…ail. Число l – кількість букв у слові - називають довжиною слова і позначають l() або ||.
Множину всіх слів у алфавіті А позначають як А*. Порожнє слово позначають ; зазначимо, що А, А*, ||=0.
Означення 31.2. Якщо слово має вигляд = 12, то 1 називають початком або префіксом слова , а 2 – його закінченням або постфіксом. Якщо при цьому 1 (відповідно, 2), то 1 називають власним початком (відповідно власним закінченням) слова .
Для слів визначена операція конкатенації або зчеплення.
Означення 31.3. Конкатенація слів та є слово , отримане виписуванням підряд спочатку всіх букв слова , а потім всіх букв слова . Зазвичай операція зчеплення ніяк не позначається.
Означення 31.4. Довільна множина L слів у деякому алфавіті А називається мовою в цьому алфавіті, L A*.
Нехай задано алфавіти А = {a1,…,an}, B = {b1,…,bm} і функція F: S B*, де S – деяка множина слів у алфавіті А, S A*. Тоді функція F називається кодуванням, елементи множини S – повідомленнями, а елементи = F(), S, B* - кодами (відповідних повідомлень). Обернена функція F-1, якщо вона існує, називається декодуванням.
Якщо |B| = m, то F називають m-ковим кодуванням. Найчастіше використовується алфавіт B = {0, 1}, тобто двійкове кодування. Саме його ми й розглядатимемо в наступних підрозділах, випускаючи слово «двійкове».
Відображення F задають якимось алгоритмом. Є два способи задати відображення F.
Алфавітне кодування задають схемою (або таблицею кодів) :
a1 1,
a2 2,
…
an n,
де ai А, i B*, i = 1,…,n. Схема задає відповідність між буквами алфавіту А та деякими словами в алфавіті В. Вона визначає алфавітне кодування так: кожному слову = ai1ai2…ail із повідомлення S поставлено у відповідність слово = i1i2…il – його код. Слова 1, …, n називають елементарними кодами.
Наприклад, розглянемо алфавіт А = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, B = {0, 1} і схему:
1 = 0 0, 1 1, 2 10, 3 11, 4 100, 5 101, 6 110, 7 111, 8 1000, 9 1001.
Ця схема однозначна, але кодування не є взаємно однозначним:
F1 (333) = 111111 = F (77),
а значить, неможливе декодування. З іншого боку, схема
1 = 0 0000, 1 0001, 2 0010, 3 0011, 4 0100, 5 0101,
6 0110, 7 0111, 8 1000, 9 1001,
відома під назвою «двійково-десяткове кодування», допускає однозначне декодування.
Рівномірне кодування з параметрами k й r задають так. Повідомлення розбивають на блоки довжиною k:
= (x1…xk)(xk+1…x2k)…(xmk+1…xpk+s),
де sk (останній блок може бути коротшим, у такому разі спосіб його кодування спеціально обумовлюють), xiA, i = 1,…, pk + s. Блоки довжиною k розглядають як «букви» якогось алфавіту (таких блоків, очевидно, nk, бо алфавіт А складається з n букв) і кодують словами в алфавіті В довжиною r за схемою рівномірного кодування k,r:
1 1,
2 2,
…
.Надлишковістю схеми k,r на символ повідомлення називають величину
.31.2. Роздільні схеми
Розглянемо схему алфавітного кодування та різні слова, складені з елементарних кодів.
Означення 31.5. Схему називають роздільною, якщо з рівності
випливає, що k= l та it = jt для кожного t = 1,…, k, тобто будь-яке слово, складене з елементарних кодів, можна єдиним способом розкласти на елементарні коди.Алфавітне кодування з роздільною схемою вможливлює однозначне декодування.
Означення 31.6. Схему називають префіксною, якщо для будь-яких i та j (i, j = 1,…,n, ij) елементарний код i не є префіксом елементарного коду j.
Теорема 31.1 (без доведення). Префіксна схема є роздільною.
Властивість префіксності достатня, але не необхідна умова роздільності схеми. Наприклад, нехай A = {a, b}, B = {0, 1}, = a 0, b 01. Схема не префіксна, але роздільна. Справді, перед кожним входженням 1 в слові 2 безпосередньо є 0. Це дає змогу виділити всі пари (01). Частина слова, що залишилась, складається із символів 0.
Щоби схема алфавітного кодування була роздільною, необхідно , щоби довжини елементарних кодів задовольняли певному співвідношенню, відомому як нерівність Мак-Міллана.
Теорема 31.2 (нерівність Мак-Міллана, без доведення). Якщо схема алфавітного кодування
роздільна, то 
, де li = |i|.Теорема 31.3 (без доведення). Якщо числа l1,…, ln задовольняють нерівність
(нерівність Мак-Міллана),то існує префіксна схема алфавітного кодування :
a1 1,
…
an n,
де li = |i|.
Наслідок 1. Нерівність Мак-Міллана – необхідна й достатня умова існування алфавітного кодування з префіксною схемою та довжинами елементарних кодів, що дорівнюють l1,…,ln.
Наслідок 2. Якщо існує роздільна схема алфавітного кодування із заданими довжинами елементарних кодів, то існує й префіксна схема з тими самими довжинами елементарних кодів.
31.3. Оптимальне кодування
Для практики важливо, щоби коди повідомлень мали по можливості найменшу довжину. Алфавітне кодування придатне для довільних повідомлень, тобто S = A*. Якщо більше про множину S не відомо нічого, то точно сформулювати задачу оптимізації важко. Однак на практиці часто доступна додаткова інформація. Наприклад, для текстів на природних мовах відомо розподілення ймовірностей (частот) появи букв у повідомленні. Використання такої інформації дозволяє строго поставити та розв’язати задачу побудови оптимального алфавітного кодування.
Нехай задано алфавіт А = {a1,…,an} і ймовірності появи букв у повідомленні P = (p1,…,pn); тут pi – ймовірність появи букви ai (ймовірність можна розглядати як частоту і обчислювати у вигляді формули f(ai)/l, де f(ai) – кількість разів появи букви ai у повідомленні, а l – загальна кількість букв у повідомленні, тобто довжина повідомлення). Не втрачаючи загальності, можна вважати, що p1 p2 … pn > 0, тобто можна одразу вилучити букви, які не можуть з’явитись у повідомленні, і впорядкувати букви за спаданням ймовірностей їх появи. Крім того, p1+ p2 + …+ pn = 1.
Означення 31.7. Для кожної роздільної схеми алфавітного кодування
величина 
, де li = |i|, i = 1,…, n називають середньою довжиною або ціною кодування за схемою для розподілу ймовірностей Р.Наприклад, для алфавітів A = {a, b}, B = {0, 1} та роздільної схеми = a 0, b 01 при розподілі ймовірностей (0.5, 0.5) ціна кодування складає 0.51 + 0.52 = 1.5, а при розподілі ймовірностей (0.9, 0.1) вона дорівнює 0.91 + 0.12 = 1.1.
Уведемо величину
, де нижню грань беруть за всіма роздільними схемами . Легко довести, що 
,де верхю оцінку дає схема з елементарними кодами з однаковою довжиною
. Звідси випливає, що для побудови кодів, у яких величина l близька до l*, можна не враховувати коди з більшим l, ніж . Отже, будемо розглядати лише схеми з 
. Позначимо p* = min(p1,…,pn), тоді
для всіх i = 1,…, n.
Звідси випливає, що є лише скінченна кількість варіантів значень l, для яких
. Отже, значення l* досягається на якійсь схемі ; його можна визначити як
.Означення 31.8. Коди, визначені схемою з l = l*, називають кодами з мінімальною надлишковістю або оптимальними кодами для розподілу ймовірностей Р.
За наслідком 2 з теорем 31.2 та 31.3 існує алфавітне кодування з префіксною схемою, яке дає оптимальні коди. У зв’язку з цим, будуючи коди, можна обмежитися префіксними схемами.
31.4. Алгоритм Шенона-Фано
Алгоритм Шеннона-Фано – один з перших алгоритмів кодування, який вперше сформулювали американські вчені Шенон та Фано. Даний метод кодування має велику подібність із алгоритмом Хаффмана, який з’явився на декілька років пізніше. Алгоритм заснований на кодах змінної довжини: символ, який зустрічається часто, кодується кодом меншої довжини і навпаки. Для того, щоби існувало декодування, коди Шенона-Фано мають володіти унікальністю, тобто, не дивлячись на їх змінну довжину, кожний код унікально визначає один закодований символ і не є префіксом будь-якого іншого коду. Тобто отриманий код є префіксним.
Код Шенона-Фано будується за допомогою дерева. Побудова цього дерева починається від кореня. Вся множина елементів, які кодуються, відповідає кореню дерева (вершині першого рівня). Вона (множина) розбивається на дві підмножини з приблизно однаковими сумарними ймовірностями. Ці підмножини відповідають двом вершинам другого рівня, які з’єднуються з коренем. Далі кожна з цих підмножин розбивається на дві підмножини з приблизно однаковими сумарними ймовірностями. Їм відповідають вершини третього рівня. Якщо підмножина містить один елемент, то йому відповідає кінцева вершина кодового дерева; така підмножина більше не розбивається. Подібним чином поступаємо до тих пір, поки не отримуємо всі кінцеві вершини. Гілки кодового дерева помічаємо символами 1 та 0.
При побудові кода Шенона-Фано розбиття множини елементів може бути виконано, взагалі кажучи, декількома способами. Вибір розбиття на рівні n може погіршити варіанти розбиття на наступному рівні (n+1) і привести до неоптимального коду в цілому. Іншими словами, оптимальна поведінка на кожному кроці шляху не гарантує оптимальності усієї сукупності дій. Тому код Шенона-Фано не є оптимальним в загальному сенсі, хоча й дає оптимальні результати при деяких розподілах ймовірностей. Для одного й того самого розподілу ймовірностей можна побудувати, взагалі кажучи, декілька кодів Шенона-Фано, і всі вони можуть давати різні результати.
Кодування Шенона-Фано є доволі старим методом і на сьогоднішній день воно не представляє собою практичного інтересу. В більшості випадків, довжина отриманої послідовності, за даним методом, дорівнює довжині послідовності при використанні методу Хаффмана. Але на деяких послідовностях все ж таки формуються неоптимальні коди Шенона-Фано, тому метод Хаффмана прийнято вважати більш ефективним.
Розглянемо приклад кодового дерева. Нехай маємо алфавіт А = {a, b, c, d, e, f}, де для кожної букви відома частота появи у тексті – f(), за якою можна визначити ймовірність p(). Частоти, ймовірності та коди букв представлені в табл. 31.1.
| Буква | Частота f | Ймовірність p | Код |
| a | 50 | 0,23 | 11 |
| b | 39 | 0,18 | 101 |
| c | 18 | 0,08 | 100 |
| d | 50 | 0,23 | 01 |
| e | 33 | 0,16 | 001 |
| f | 26 | 0,12 | 000 |
Табл. 31.1.
Кодове дерево, яке отримуємо під час роботи алгоритму, зображено на рис. 31.1.
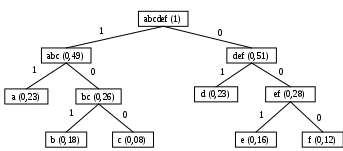
Рис. 31.1.
Підрахуємо l: 0,232 + 0,183 + 0,083 + 0,232 + 0,163 + 0,123 = 2,54.
31.4. Алгоритм Хаффмана
Розглянемо декілька властивостей оптимальних кодів.
Теорема 31.4. В оптимальному коді букву з меншою ймовірністю її появи не можна закодувати коротшим словом. Інакше кажучи, для оптимального коду з того, що pi<pj випливає, що li lj.
Доведення. Припустимо протилежне: нехай є дві букви ai та aj такі, що pi<pj і li < lj. Поміняємо місцями i та j у схемі кодування. Тоді середня довжина елементарних кодів змінить на
,тобто зменшиться, що суперечить оптимальності коду. ►
Очевидно, що якщо код оптимальний, то можна перенумерувати букви алфавіту А і відповідні елементарні коди i, що p1 p2 … pn та l1 l2 … ln. Далі ми будемо розглядати схеми кодування, де коди впорядковані таким чином.
Теорема 31.5. В оптимальному коді є два елементарні коди з найбільшою довжиною ln, які відрізняються лише останніми символами.
Доведення. Припустимо, що це не так. Тоді можна відкинути останній символ елементарного коду n, не порушуючи властивості префіксності. При цьому, очевидно, зменшиться середня довжина елементарного коду. Це суперечить твердженню, що код оптимальний. ►
Теорема 31.6. Існує такий оптимальний код, у якому елементарні коди двох найменш імовірних букв an та an-1 відрізняються лише останніми символами.
Доведення. За теоремою 31.5 знайдеться елементарний код t, який має ту саму довжину, що й n, і відрізняється від нього лише останнім символом. Із теореми 31.4 випливає, що lt = lt+1 = … = ln. Якщо t n-1, то можна поміняти місцями t та n-1, не порушуючи нерівності l1 l2 … ln. ►
Теорема 31.6 дає змогу розглядати лише такі схеми алфавітного кодування, у яких елементарні коди n-1 та n (для двох найменш імовірних букв an-1 та an) мають найбільшу довжину й відрізняються тільки останніми символами. Це означає, що листки n-1 та n кодового дерева оптимального коду мають бути з'єднані в одній вершині попереднього рівня.
Розглянемо новий алфавіт A1 = {a1, …, an-2, a} із розподілом ймовірностей P1 = {p1, …, pn-2, p}, де p = pn-1 + pn. Його одержано з алфавіту А об'єднанням двох найменших букв an-1 та an в одну букву а з ймовірністю p = pn-1 + pn. Говорять, що А1 отримано стисненням алфавіту А.
Нехай для алфавіту А1 побудовано схему 1 з елементарними кодами 1, 2, …, n-2, . Схемі 1 можна поставити у відповідність схему з елементарними кодами 1, 2, …, n-2, n-1, n для початкового алфавіту А, узявши n-1 = 0, n = 1 (тобто елементарні коди n-1 та n одержують з елементарного коду приписуванням справа відповідно 0 та 1). Процедуру переходу від 1 до називають розщепленням.
Теорема 31.7 (без доведення). Якщо схема 1 оптимальна для алфавіту А1, то схема оптимальна для алфавіту А.
З цієї теореми випливає такий метод побудови оптимальної схеми алфавітного кодування. Спочатку послідовно стискають алфавіт А до отримання алфавіту з двох букв, оптимальна схема кодування для якого очевидна: першу букву кодують символом 0, другу – символом 1. Потім послідовно розщеплюють одержану схему. Очевидно, що отримана в результаті схема префіксна.
Цей метод кодування запропоновано 1952 р. американським математиком Д. Хаффманом.
Розглянемо використання цього алгоритму для попереднього прикладу з розділу 31.3. У процесі побудуємо так зване дерево Хаффмана. Це є бінарне дерево, що відповідає оптимальному коду, яке будується знизу вгору, починаючи з |А| = n листків за n – 1 крок (злиття). Під час кожного кроку (злиття) дві вершини з найменшими ймовірностями об'єднуються однією вершиною вищого рівня, яка буде мати ймовірність, що дорівнює сумі ймовірності початкових двох вершин. При цьому нові ребра позначають 0 та 1.
Збудоване дерево зображено на рис. 31.2.
Після застосування алгоритму отримуємо таку схему кодування:
| Буква | Код |
| a | 00 |
| b | 010 |
| c | 111 |
| d | 10 |
| e | 011 |
| f | 110 |
Середня довжина побудованого коду, як і у випадку алгоритму Шенона-Фано, становить 0,232 + 0,183 + 0,083 + 0,232 + 0,163 + 0,123 = 2,54.
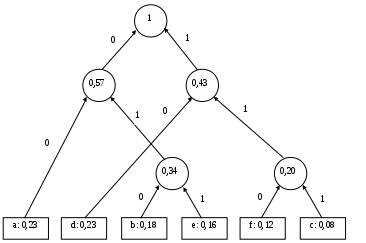
Рис. 31.2