МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ “ЛЬВІВСЬКА ПОЛІТЕХНІКА”
Інститут комп’ютерних наук та інформаційних технологій
Кафедра систем штучного інтелекту
Лабораторна робота №7
з дисципліни
«Чисельні методи»
Виконала:
студентка групи КН-212
Казьоннікова Ніколетта
Викладач:
Мочурад Л.І.
Львів – 2020 р.
Тема: Обчислення значень визначеного інтегралів за допомогою узагальнених квадратурних формул.
Мета – набути навиків вирішення задач чисельного інтегрування на основі використання узагальнених квадратурних формул трапеції та Сімпона.
Програма
Обчислити наближене значення інтегралу за узагальненою
1. формулою трапеції.
2. Формулою Сімпсона.
Крок інтегрування визначається формулою
. Значення кроку інтегрування, що забезпечує задану точніть визначити за допомогою подвійного перерахунку з поділом відрізку на n та 2n частин. Точність рішення 0.5*10-6. Варіанти індивідуальних завдань приведені в табл. 1. Інтегрування за формулою трапеції реалізовують парні номери у журналі викладача, а за формулою Сімпсона – непарні
Код програми:
#include
#include
#include
using namespace std;
double f(double x)
{
return 1/(0.35*pow(cos(0.6*x),2)+pow(sin(0.6*x),2));
// return (x*sqrt(0.7*pow(x,2)+1.2*x+2.1))/pow(2.1+x,2);
}
int main() {
double a, b, eps=0.0001;
a=0.1; b=1.1;
//a=0.3; b=1.3;
double I=eps+1, I1=0;
for (int N=2; (N<=4)||(fabs(I1-I)>eps); N*=2)
{
double h, sum2=0, sum4=0, sum=0;
h=(b-a)/(2*N);
for (int i=1; i<=2*N-1; i+=2)
{
sum4+=f(a+h*i);
sum2+=f(a+h*(i+1));
}
sum=f(a)+4*sum4+2*sum2-f(b);
I=I1;
I1=(h/3)*sum;
}
cout <
}
Результати для двох інтегралів:
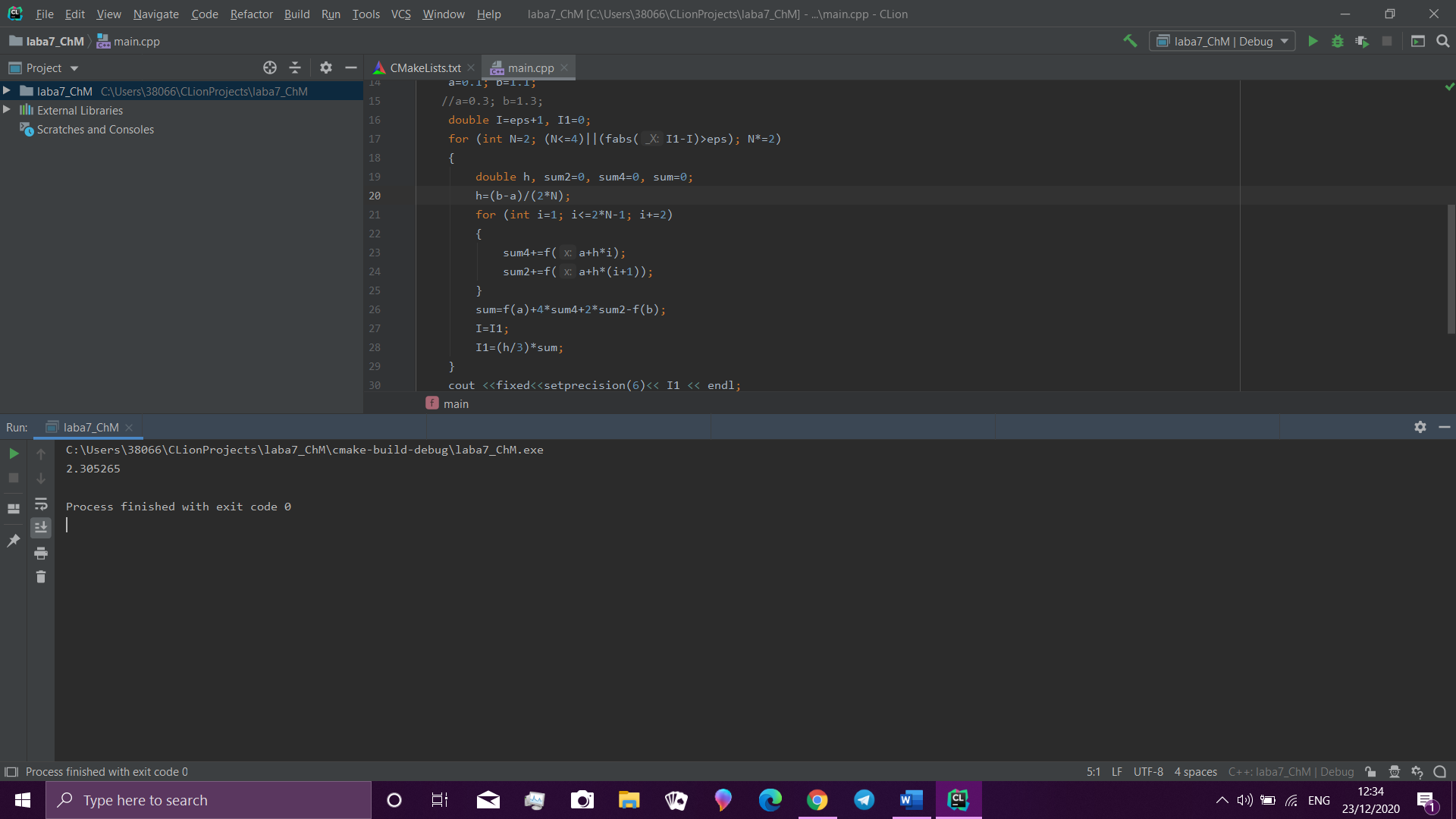
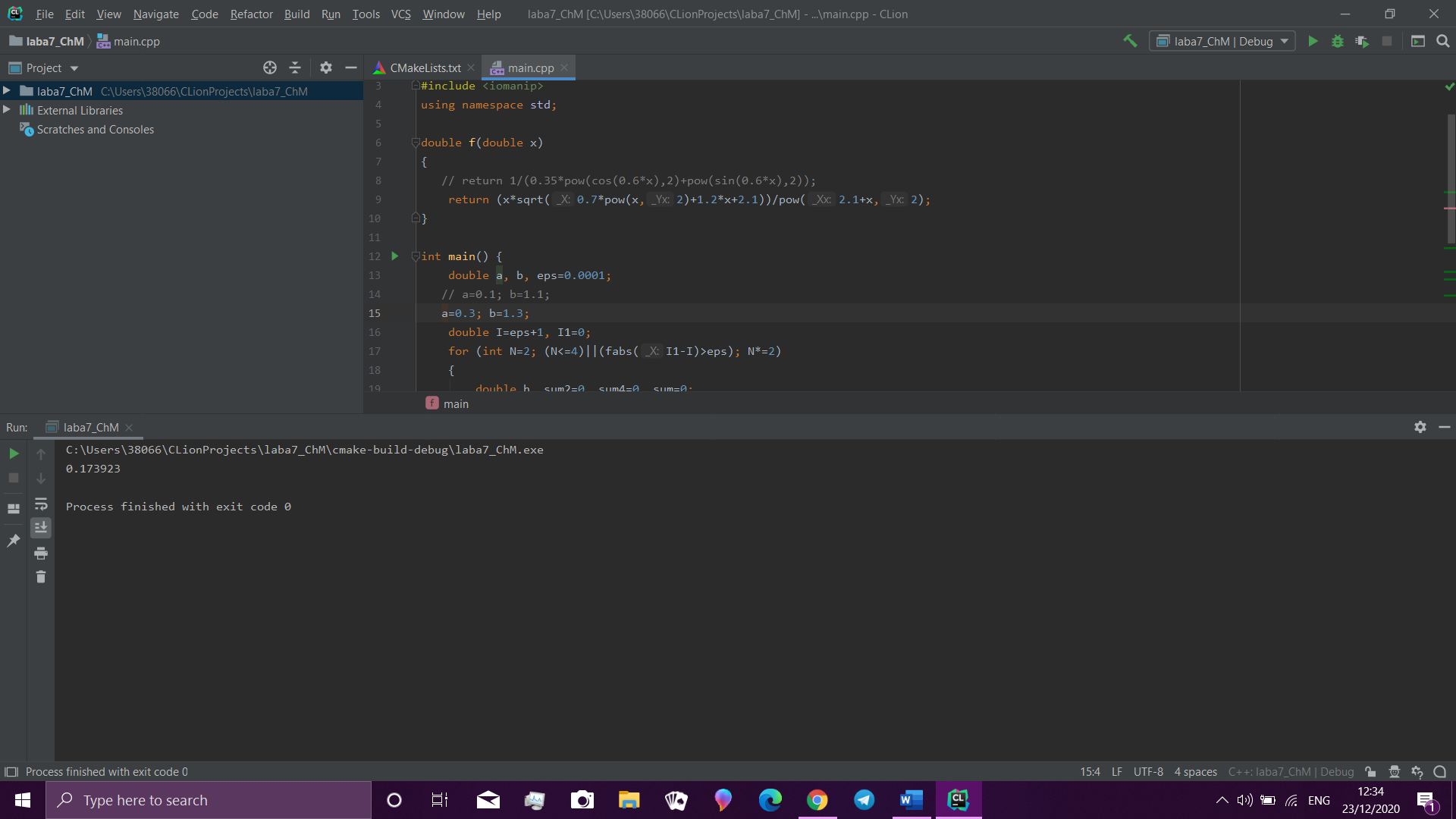
Висновки: в ході лабораторної я набула навиків вирішення задач чисельного інтегрування на основі використання узагальнених квадратурних формул трапеції та Сімпона.