
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЛАБОРОТОРНОЙ РАБОТЫ № 10 «МЕТОД ЭЛЕКТРА»
САБИРОВ А. В. ИТВ-4-06, Метляев Л. В. ИТВ-4-06
Описание метода
Цель применения методов ЭЛЕКТРА - сужение паретовского множества альтернатив. Делается это так. Для каждого из критериев (предполагается, что они - числовые) определяется по результатам опроса ЛПР «вес» - число, характеризующее важность соответствующего критерия. Во всех модификациях метода ЭЛЕКТРА делается попытка получения от ЛПР информации качественного характера об относительной важности критериев (высказывания типа «критерии 3 и 4 имеют одинаковую важность и рассматриваемые совместно имеют большую важность, чем критерий 1») и преобразования ее в количественную, числовую. Проблема здесь состоит в том, что сделать это можно в общем случае множеством способов.
Далее, для каждой пары сравниваемых альтернатив x=(x1,.....,xn) и y=(y1,.......,yn) (где n - число критериев, а для дальнейшего мы через I обозначим множество критериев, т.е. I= n) выполняются такие действия. Множество I разбивается на 3 подмножества:
I+(x,y) - множество критериев, по которым х превосходит у: x>y.
I- (x,y) - множество критериев, по которым у превосходит х: у>х.
I=(x,y) - множество критериев, по которым х и у имеют одинаковые оценки: у=х.
Определяется относительная важность P
Pi. - коэффицент относительной важности i-го критерия. Теперь мы готовы сформировать правило сравнения альтернатив х и у:
- в методе ЭЛЕКТРА-I оно таково:
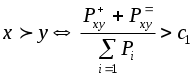 ,
, - в методе ЭЛЕКТРА-II оно модифицировано:
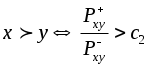 , (c 21).
, (c 21).Всё рассмотренное до сих пор весьма традиционно, и содержит традиционную погрешность в логических рассуждениях: получается, что очень маленький выигрыш по одному критерию может компенсировать очень большой проигрыш по другому. Для того чтобы эту трудность (погрешность) исключить, в методе «Электра» пытаются НЕ сравнивать очень сильно различающиеся альтернативы. Они просто объявляются несравнимыми. Вводится так называемый «индекс несогласия»:
х и у несравнимы, если dxyd,
где dxy - расстояние между х и у определяется как maxixi - yi, a d - т.н. порог индекса несогласия. Теперь введённые нами раньше соотношения модифицируются так:
в ЭЛЕКТРА-I
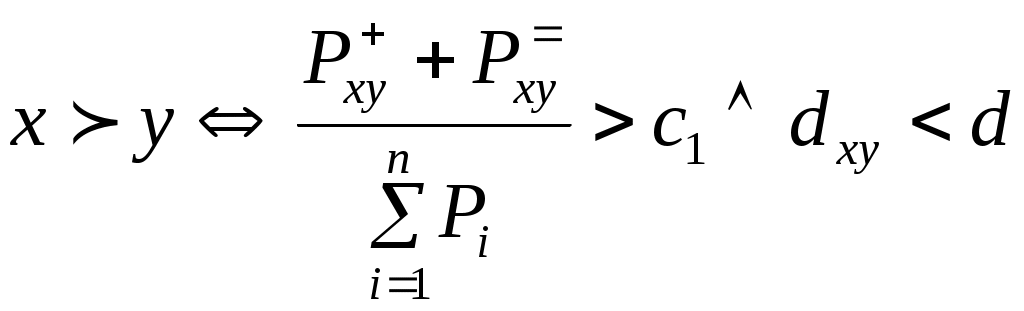 .
.в ЭЛЕКТРА-II
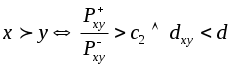 .
.Получаемое бинарное отношение, очевидно, уже не будет обладать свойством полноты. Это учитывается и в окончательном результате ЭЛЕКТРА. Он таков. В исходном паретовском множестве выделяется т.н. ядро, состоящее из недоминируемых по новому (описанному нами) бинарному отношению элементов и всех, несравнимых с ними (т.е. любой элемент, не вошедший в ядро, доминируется хотя бы одним элементом ядра). Отметим, что, к сожалению, нельзя гарантировать цикличность отношения, получаемого описанным способом.
Пример выполнения лабораторной работы
Рассмотрим данный метод на примере решения о покупке автомобиля.
Сначала составляют таблицу критериев, по которым будут оценивать проекты (см. табл. 1).
| Таблица 1 Таблица критериев для оценки проектов | |||||||||||||||||||||||||
|
Далее эксперт составляет таблицу оценок проектов (автомобилей). Например, для 7-ми автомобилей эксперт заполняет таблицу так, как показано в табл. 2.
| Таблица 2. Таблица оценок проектов по критериям | |||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||
Рассматриваем все пары проектов i и j. Если по какому-либо критерию i-ый проект лучше, чем j-ый, то соответствующий критерию вес прибавляется к Pij (эти баллы символизируют выбор «За»), в противном случае — к Nij (эти баллы символизируют выбор «Против»). То же самое справедливо для j-го проекта: если j-ый проект оказывается лучше, чем i-ый, то соответствующий критерию вес прибавляется к Pji, в противном случае — к Nji (обратите внимание на порядок следования индексов j и i у P и N). Если повстречалось одинаковое для i-го и для j-го проектов значение критерия, то оно пропускается. Затем, когда по паре i и j рассмотрены все критерии, находятся отношения Dij = Pij/Nij и Dji = Pji/Nji. Значения D ≤ 1 отбрасываются. Заметим, что Dji = 1/Dij (и наоборот), таким образом, вычисления можно несколько упростить.
Рассмотрим, для примера, проекты 2 и 4 (i = 2, j = 4). По критерию «Цена» (вес критерия — 5 баллов) проект 2 хуже проекта 4; по критерию «Комфортность» (вес — 4 балла) проект 2 лучше проекта 4; по критерию «Скорость» (вес — 3 балла) проект 2 хуже проекта 4; по критерию «Дизайн» (вес — 3 балла) проект 2 лучше проекта 4. Таким образом, имеем:
P24 = 0 + 4 + 0 + 3 = 7;
N24 = 5 + 0 + 3 + 0 = 8;
D24 =P24/N24 =7/8 = 0.875 < 1 — отбрасываем;
P42 = 5 + 0 + 3 + 0 = 8;
N42 = 0 + 4 + 0 + 3 = 7;
D42 =P42/N42 =8/7 = 1/0.875 = 1.14 > 1 — принимаем.
Рассмотрим, для примера, проекты 1 и 2 (i = 1, j = 2). По критерию «Цена» проект 1 хуже проекта 2; по критерию «Комфортность» проекты 1 и 2 одинаковы, поэтому ничего не делаем; по критерию «Скорость» проект 1 лучше проекта 2; по критерию «Дизайн» проекты 1 и 2 одинаковы, поэтому ничего не делаем. Таким образом, имеем:
P12 = 0 + 0 + 3 + 0 = 3;
N12 = 5 + 0 + 0 + 0 = 5;
D12 =P12/N12 =3/5 = 0.6 < 1 — отбрасываем;
P21 = 5 + 0 + 0 + 0 = 5;
N21 = 0 + 0 + 3 + 0 = 3;
D21 =P21/N21 =5/3 = 1/0.6 = 1.67 > 1 — принимаем.
Все остальные пары рассчитываются аналогично.
Составляем матрицу, внося вычисленные (и принятые) значения D. Матрица имеет смысл предпочтений проектов между собой. Для нашего примера матрица выглядит следующим образом (см. табл. 3).
| Таблица 3. Полная матрица предпочтений проектов, составленная методом «Электра» | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Задаемся порогом принятия решения, например C = 1.33, и оставляем в матрице те числа, которые больше или равны значению порога C. Таким образом, матрица разрежается (см. табл. 4).
| Таблица 4 Матрица предпочтений проектов при пороге C = 1.33 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
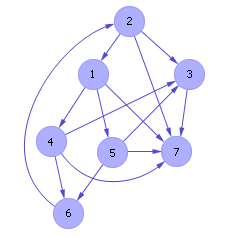
По матрице строится граф предпочтений (см. рис.1). Из графа, построенного по табл. 36.13, видно, что проект 1 лучше проектов 4, 5, 7; проект 2 лучше проектов 1, 3, 7; проект 3 лучше проекта 7; проект 4 лучше проектов 3, 6, 7; проект 5 лучше проектов 3, 6, 7; проект 6 лучше проекта 2.
| ||
| Рис. 1. Вид графа предпочтений для случая порога принятия решений C = 1.33 |
Очевидно, что решение не получено, так как в графе присутствуют петли. Например, 2 лучше 1, 1 лучше 5, 5 лучше 6, 6 лучше 2. Назначим порог отбора предпочтений C = 1.4 (это соответствует тому, что мы попробуем учесть только более сильные связи в графе, не отвлекаясь на малозначимые расхождения в проектах). Таким образом, матрица еще разрежается. В ней остаются только самые сильные связи (см. табл. 5).
| Таблица 5. Матрица предпочтений проектов при пороге C = 1.4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
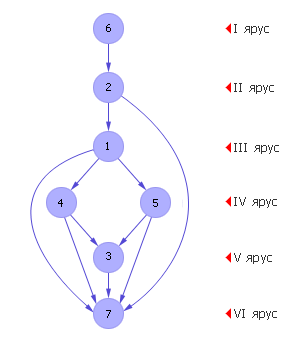
По матрице строится граф предпочтений (см. рис. 2). По графу и табл. 36.14 видно, что проект 1 лучше проектов 4, 5, 7; проект 2 лучше проектов 1, 7; проект 3 лучше проекта 7; проект 4 лучше проектов 3, 7; проект 5 лучше проектов 3, 7; проект 6 лучше проекта 2. Как видим из рис. 36.6, при C = 1.4 граф получился в таком виде, в котором он легко приводится к ЯПФ, следовательно, решение получено.
| ||
| Рис. 2. Вид графа предпочтений для случая порога принятия решений C = 1.4 |
Петель в графе нет, при этом граф остался целостным. Решение говорит нам о том, что лучший проект — 6. На втором месте — проект 2, на третьем месте — проект 1, четвертое и пятое место делят проекты 4 и 5, на шестом месте — проект 3, на седьмом месте — проект 7.
Примечания
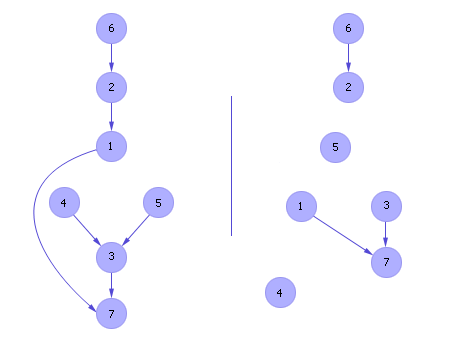
Как можно видеть, порог C подбирается эмпирически. При малом пороге C (в матрице много компонент), в графе содержится много петель. Увеличивая порог C, можно добиться уменьшения количества связей и устранения малозначащих связей и петель. Однако нужно иметь в виду, что при очень высоком значении порога C граф распадется на несколько отдельных графов из-за отсутствия необходимых связей; в качестве иллюстрации см. рис. 3: при пороге C = 1.67 проекты 4 и 5 остаются без входящих стрелок, и поэтому становится неясно, какой же проект — 6-ой, 4-ый или 5-ый — является наилучшим. А при пороге C = 2 граф распадается на четыре не связанных подграфа.
Если граф не будет найден ни при каких значениях порога C, то следует изменить веса критериев и всю процедуру провести снова.
Если разумное изменение весов не помогает, и проекты все еще путаются (петли в графе), то надо детализировать проблему, добавив критерии.
| ||
| Рис. 3. Вид графа предпочтений для случая порога принятия решений C = 1.67 (слева) и C = 2 (справа) |