
Метод векторів та його застосування
Вступ
Поняття вектора є одним із фундаментальних понять сучасної математики. Його можна визначити по-різному: як напрямлений відрізок, як упорядковану пару точок, що є кінцями напрямленого відрізка, як множину однаково напрямлених відрізків однакової довжини, як упорядковану пару чисел, як паралельне перенесення.
Уперше поняття вектора як напрямленого відрізка знайшло застосування в механіці для зображення фізичних векторних величин: швидкості, прискорення, сили, моменту сили тощо. Високий ступінь наочності і простота геометричних операцій над векторами як напрямленими відрізками сприяли тому, що поняття вектора знайшло загальне визнання і застосування в інших розділах фізики: в кінематиці, статиці, динаміці точки і динаміці системи, в теорії потенціалу та гідродинаміці, а також стало одним із основних понять таких наук, як векторна алгебра, векторний аналіз, теорія поля, тензорний аналіз тощо.
Проте хоча поняття вектора знайшло перше застосування в фізиці, це математичне поняття, усі операції над якими виконуються за законами математики.
Вектор як математичне поняття міцно ввійшов у шкільну математику, у різні нематематичні науки. В школі за допомогою векторного метод розв’язується багато різноманітних задач, які не мають іншого способу розв’язання.
Саме тому вивчення поняття вектора є дуже важливим в сучасних умовах розвитку математичних наук.
1. Поняття вектора
В елементарній геометрії, як відомо, відрізком AB називається сукупність всіх точок прямої, що лежать між A і B. Точки A і B називаються кінцями відрізка. При цьому, очевидно, порядок, в якому беруться кінці відрізка, несуттєвий. Однак при використанні геометрії у вивченні фізики, особливо механіки, часто доводиться розглядати напрямлені відрізки, тобто відрізки, для яких вказані початкова і кінцева точки. Тобто AB і BA геометрично один і той же відрізок, то, розглядаючи їх як напрямлені відрізки, ми повинні враховувати, що вони задають різні об’єкти.
Означення 1. Відрізок АВ називається напрямленим, якщо береться до уваги порядок його кінцевих точок. Перша точка (А) називається його початком, а друга (В) – його кінцем.
Позначають напрямлений відрізок так: АВ.
Означення 2. Довжиною напрямленого відрізка називається
довжина відрізка АВ. Позначають: . Звідси = АВ =
Означення 3. Напрямлені відрізки АВ і CD називаються однаково напрямленими (спів напрямленими), якщо однаково напрямлені промені АВ і CD, і протилежно напрямленими, якщо ці промені протилежно напрямлені.
Означення 4. Вектором називається множина однаково напрямлених (спів напрямлених) відрізків однакової довжини.
Означення 4.1. Вектором називається напрямлений відрізок, тобто відрізок, для якого вказано, яка з обмежуючих його точок рахується першою, яка – другою. Перша точка напрямленого відрізка називається початком вектора, а друга точка – кінцем.
Напрямок вектора на кресленні відмічається стрілкою, оберненою гострим кінцем до кінця вектора. В тексті вектор записується двома великими літерами латинського алфавіту зі спільною рискою зверху, при цьому перша з них позначає початок, друга – кінець вектора. Наприклад, , (мал. 1.a), причому А, C – відповідно початки, а В, D – кінці даних векторів. В деяких випадках вектор позначається також однією малою літерою, наприклад, a, b, c,… (мал. 1.b).
| | | | | | |
| | 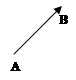 | | | | |
| | |  | | | |
| | | | | ||
| | | | |
мал. 1.a мал. 1.b
Означення 5. Вектори і називаються однаково напрямленими (спів напрямленими), якщо спів напрямлені відповідні їм напрямлені відрізки і (мал. 2.a), і протилежно напрямленими, якщо напрямлені відрізки і протилежно напрямлені (мал. 2.b).
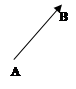
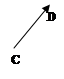
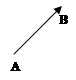
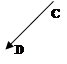
мал. 2.a мал. 2.b
Означення 6. Довжиною (модулем) вектора називається довжина будь-якого представника класу спів напрямлених відрізків, який визначає цей вектор.
Інакше кажучи, довжиною вектора називається довжина напрямного відрізка, який зображає цей вектор.
Модуль вектора позначають , а вектора АB – .
Вектор, початок якого збігається з його кінцем, називається нульовим вектором, позначають або . Нульовий вектор не визначає ніякого напряму, а його довжина вважається рівною нулю.
Вектор, довжина якого дорівнює одиниці, називається одиничним вектором, або ортом.
Рівність векторів
Означення 1. Два вектори називаються рівними, якщо множини відповідних їм напрямлених відрізків збігаються. Пишуть: = .
Всі нульові вектори вважаться рівними один одному.
Із цього означення випливає така ознака рівності двох векторів.
Теорема 1. (перша ознака рівності двох векторів).
Для того щоб два вектори були рівними, необхідно і достатньо, щоб вони були однаково напрямленими і мали рівні довжини.
Доведення:
1. Необхідність. Нехай вектори і рівні. Доведемо, що і = .
Якщо = , то, за означенням 1, множини напрямлених відрізків, які відповідають цим векторам, збігаються. Тому , = . Звідси , = , що й треба було довести.
2. Достатність. Нехай , = . Доведемо, що = . Якщо, , = , то , = , тобто і належать одній і тій же множині однаково напрямлених відрізків рівної довжини. А це означає, що = . Теорему доведено.
Наслідок. Два вектори, кожен з яких дорівнює третьому, рівні між собою.
Теорема 2. (теорема про відкладання вектора).
Від будь-якої точки простору можна відкласти вектор, рівний даному, і до того ж єдиний.
Доведення: Нехай даний вектор зображається напрямленим відрізком . Виберемо у просторі довільну точку О, сполучимо точку В з точкою О і позначимо середину відрізка ОВ через С (мал. 3). Проведемо

відрізок АС і відкладемо на його продовженні відрізок CM=АС. Чотирикутник АВМО є паралелограмом, бо його діагоналі точкою перетину діляться пополам. Звідси випливає, що промені АВ і ОМ однаково напрямлені, а відрізки АВ і ОМ рівні. Отже, = = .

Доведемо тепер, що цей вектор єдиний. Припустимо, що існує інший вектор = , відмінний від . Але ж і = , тому = . Отже, ,
Означення 2. Два вектори називаються протилежними, якщо вони протилежно напрямлені і мають рівні довжини. Вектор, протилежний до , позначається - (мал. 4). Очевидно, =- , – (- )= .
Додавання векторів, властивості операції додавання векторів

Введемо операцію додавання векторів, яка відіграє важливу роль в векторній алгебрі.
Означення. Нехай задано два вектори і . Від деякої точки A відкладемо вектор = , потім від точки B відкладемо вектор = . Вектор = називається сумою векторів і і позначається так: = + (мал. 5). Помітимо, що для знаходження двох неколінеарних векторів доводиться будувати трикутник. Тому вказане правило додавання векторів називають правилом трикутника. Це правило можна сформулювати так: для будь-яких трьох точок A, B і C + = , або: сумою векторів і євектор , який сполучає початок вектора з кінцем вектора при умові, що вектор відкладено від кінця вектора .
З цього правила випливає правило паралелограма: якщо вектори і відкладені від спільного початку O, = , = (мал. 6) і на них побудовано паралелограм OACB, то сумою векторів + є вектор = , який виходить з того ж початку і збігається з діагоналлю OC паралелограма.
Розглянемо властивості операції додавання векторів.

Властивість 1. Операція додавання векторів комутативна, тобто для будь-яких векторів і : + = + .
 Доведення: За правилом трикутника маємо (мал. 7):
Доведення: За правилом трикутника маємо (мал. 7):Властивість 2. Операція додавання векторів асоціативна, тобто для будь-яких векторів , , : ( + )+ = +( + )
Доведення: Візьмемо довільну точку A і від неї відкладемо вектори = , = , = (мал. 8). Тоді + = , ( + )+ = ; + = ; +( + )= . Отже, ( + )+ = +( + ).

Множення вектора на число
Означення. Добутком вектора на дійсне число α називається вектор , який задовольняє такі умови:
1) = * ;
2) , якщо α >0, і , якщо α <0.
Такий вектор позначається = α .
Операція добутку вектора на число має такі властивості.
Властивість 1. α* =0* = для будь-якого дійсного числа α і будь-якого вектора . Ця властивість випливає з умови 1) означення.
Властивість 2. Для будь-якого вектора 1* = ; -1* =- . Ця властивість випливає безпосередньо з означення.
Властивість 3. Для будь-якого вектора і будь-яких дійсних чисел α і β: α(β )=(αβ) .
Доведення. Нехай α(β )= , (αβ) = . Доведемо, що = . Маємо:
= *
=
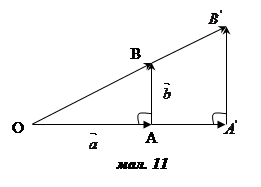
Отже, = . Покажемо, що . Якщо α і β одного знаку, то вектор однаково напрямлений з і однаково напрямлений з .Отже, . У випадку коли числа α і β протилежних знаків, , . Отже, також , що й треба було довести.
Властивість 4. Операція множення вектора на число дистрибутивна відносно додавання векторів, тобто α( + )=α +α , для , і α R.
Доведення. Нехай α > 0. Відкладемо вектори = , = ,

Аналогічно розглядається випадок, коли α <0 (мал. 12).
Випадок α = 0 тривіальний. Отже, α ( + ) = α +α .
Властивість 5. Операція множення вектора на число дистрибутивна відносно додавання чисел, тобто (α+β) =α +β , і α, β R.
Доведення. Розглянемо два можливих випадки: αβ >0 і αβ <0 (випадок αβ=0 не викликає труднощів).
1. Нехай αβ >0, тобто числа α і β одного знаку. Тоді вектори (α+β) і α +β однаково напрямлені. Крім того,
Отже,
2. Нехай αβ <0, тобто числа α і β різних знаків. Якщо α = -β, то (α+β) =(-β+β) =0 =0; α +β = -β + β =0, отже, властивість справджується.
Якщо α -β, тоді –α, α+β або –β, α+β одного знаку. Нехай, наприклад, -α, α+β одного знаку. Тоді за доведеним (-α) + (α+β) =(-α+α+β) =β (α+β) = α +β , що і треба було довести.
Колінеарність векторів
Означення. Два ненульових вектори і називається колінеарними , якщо відповідні їм напрямлені відрізки паралельні або лежать на одній прямій.
Позначення: || (мал. 13).
Очевидно, колінеарні вектори або однаково напрямлені (мал. 13а), або протилежно напрямлені (мал. 12b). Нульовий вектор вважається колінеарним будь-якому вектору. Тому, якщо відомо, що деякі два вектори неколінеарні, то жоден з них не є нульовим вектором.
Теорема . (перша ознака колінеарності двох векторів). Два ненульових вектори і колінеарні тоді і тільки тоді, коли існує деяке число α таке, що =α . /1/.
Лінійна залежність векторів
Означення. Система векторів
Якщо ж рівність /4/ справджується тільки при = =…= = 0, то дана система векторів називається лінійно незалежною.
Сума + + … + називається лінійною комбінацією векторів
Розглянемо деякі властивості лінійної залежності векторів, які будуть потрібні надалі.
Властивість 1. Система векторів лінійно залежна тоді і тільки тоді, коли хоча б один з векторів є лінійною комбінацією інших векторів цієї системи.
Доведення.
1. Необхідність. Нехай система векторів
При цьому принаймні одне з чисел , ,…, не дорівнює нулю. Нехай, наприклад, 0. Тоді з рівності /5/ дістанемо:
= –
Отже, вектор є лінійною комбінацією векторів , ,… ,
3. Достатність. Нехай у даній системі векторів вектор є лінійною комбінацією інших векторів:
= + + … + +
Цю рівність можна записати так:
+ + … + + (-1) +
У цій рівності коефіцієнт біля відмінний від нуля, тому дана система векторів лінійно залежна.
Властивість 2. Якщо частина даної системи векторів лінійно залежна, то і вся система векторів лінійно залежна.
Властивість 3. Якщо система векторів лінійно незалежна, то будь-яка її частина також лінійно незалежна.
Ця властивість безпосередньо випливає із властивості 2, бо якби деяка частина даної системи векторів була лінійно залежною, то і вся система була б лінійно залежною.
Властивість 4. Система лінійно незалежних векторів не містить нульового вектора.
Якщо в деякій системі векторів є нульовий вектор: ,
виконується рівність 1* + 0* +… + 0* =0. 1 0, тому така система є лінійно залежною, а, отже, система лінійно незалежних векторів не може містити нульового вектора.
Для системи двох і трьох векторів поняття лінійної залежності тісно пов'язане з колінеарністю і компланарністю векторів. Справедливі такі теореми.
Теорема 1. Два вектори і лінійно залежні тоді і тільки тоді, коли вони колінеарні.
У векторних просторах розглядається поняття базису векторного простору і розмірності . Введемо означення цих понять.
Означення: базисом векторного простору називається система векторів, яка задана в певному порядку і задовольняє умови:
1) ця система векторів лінійно незалежна;
2) будь-який інший вектор із даного векторного простору є лінійною комбінацією даної системи векторів.
Інакше кажучи, базисом векторного простору називається максимальна система лінійно незалежних векторів даного векторного простору.
Означення: розмірністю векторного простору називається число векторів базису, тобто максимальна кількість лінійно незалежних векторів.
З попередніх теорем випливає, що базисом побудованого нами векторного простору є будь-яка система трьох не компланарних векторів, взятих у певному порядку. Справді, система будь-яких трьох некомланарних векторів лінійно незалежна, а за теоремою про розклад вектора за трьома не компланарними векторами будь-який вектор із даного векторного простору є лінійною комбінацією даної системи векторів.
Тому розмірність даного простору дорівнює трьом. У зв’язку з цим побудований нами векторний простір називається тривимірним векторним простором.
Означення: нехай L – непорожня множина векторів із векторного простору . Множина L називається векторним підпростором простору , якщо виконуються такі умови:
1) якщо L, L, то + L;
2) якщо L, то і α L α R.
Тобто підмножина L простору буде векторним підпростором простору , якщо вона сама є векторним простором.
Скалярний добуток векторів
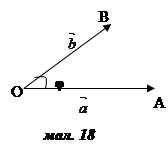
Нехай , − ненульові вектори. Відкладемо від деякої точки O вектори
Означення: скалярним добутком двох векторів називається число, яке дорівнює добутку їх довжин на косинус кута між ними: = cos( , ).
Теорема: скалярний добуток векторів ( , , ), ( , , ), заданих в ортонормованому базисі, обчислюються за формулою:
= + + . /6/

Висновок
Таким чином в своєму рефераті на тему «Метод векторів та його застосування» я подав короткі теоретичні відомості про поняття вектора, рівносильність векторів, додавання, віднімання та множення вектора на число, колінеарність, компланарність, координати вектора, скалярний добуток. Метод векторів широко застосовується в різних галузях науки (математиці, фізиці). Часто його застосування значно полегшує розв’язування деяких задач, а інших випадках задачу взагалі неможливо розв’язати іншим способом.
Підготував реферат Древніцький Артем Володимирович, 2К-19