
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ДНІПРОВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ ІМЕНІ ОЛЕСЯ ГОНЧАРА
ЕКОНОМІЧНИЙ ФАКУЛЬТЕТ
ЛАБОРАТОРНА РОБОТА №1
на тему:
«Лінійне програмування. Складання економіко-математичних моделей задач лінійного програмування»
Студентки 2-го курсу
денної форми навчання
Каліберди Мар’яни Сергіївни
Група: ЕП-19-1.
Перевірив: Катан В.О.
ДНІПРО – 2020
ЗАДАЧА №12
12. Управління міським автобусним парком вирішило провести дослідження можливості більш раціональної організації своєї роботи з метою зниження інтенсивності внутрішньоміського руху. Збір і обробка необхідної інформації дозволили зробити висновок, що мінімальна кількість автобусів істотно міняється протягом доби (рис.1). Тривалість безперервного використання автобусів на лінії дорівнює 8 год на добу (з урахуванням необхідних витрат часу на поточний ремонт і обслуговування). Графік змін, що перекриваються, представлений на рис.2.
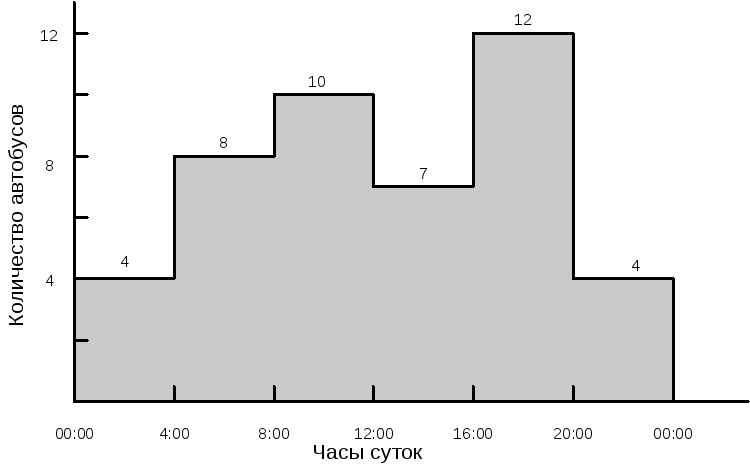
Рис.1. Мінімально необхідна кількість автобусів на лінії
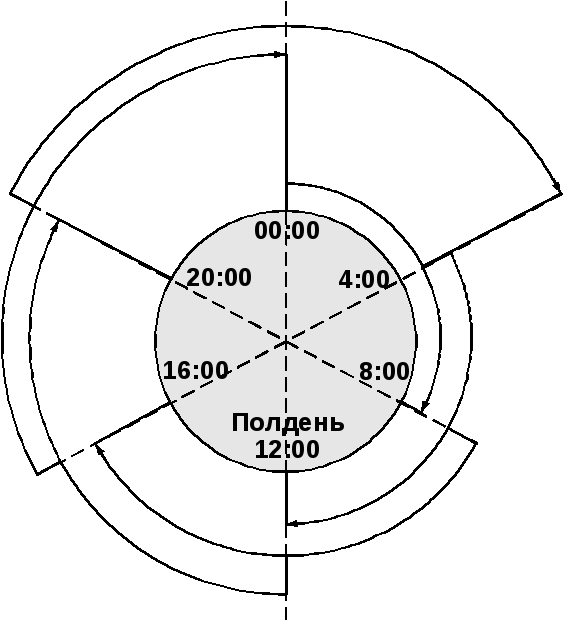
Рис.2. Графік змін, які перекриваються
Побудуйте математичну модель, що дозволяє дізнатися, яку кількість автобусів необхідно випускати на лінію в кожній із змін при умові, що загальна кількість автобусів, які виходять на лінію протягом доби, повинна бути мінімальною.
Словесне формулювання задачі: потрібно знайти спосіб розподілу кількості автобусів, які потрібно випускати на лінію в кожній із змін при умові, що загальна кількість автобусів, які виходять на лінію протягом доби, повинна бути мінімальною.
Побудова математичної моделі:
1) Змінні задачі. Нехай X1 - зміна 1, X2 - зміна 2, X3 - зміна 3, X4 - зміна 4, X5 - зміна 5, X6 - зміна 6.
Отримуємо наступні рівняння:
X1 + X6>= 4,
X1 + X2>=8,
X2 + X3>=10,
X3 + X4>=7,
X4 + X5>=12,
X5 + X6>=4,
X1, X2, X3, X4, X5, X6>=0.
2) Цільова функція. Метою розв’язання задачі є виконання плану з випуском мінімальної кількості автобусів на лінію за добу задля досягнення зниження інтенсивності внутрішньоміського руху. Таким чином ЦФ має вигляд:
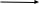
Z(x) = X1+X2+X3+X4+X5+X6 > min
3) Обмеження:
Тривалість безперервного використання автобусів на лінії дорівнює 8 год на добу (з урахуванням необхідних витрат часу на поточний ремонт і обслуговування).
Мінімально необхідна кількість автобусів необхідна на лінії у зміну №5 – 12 автобусів.
На лінії не може бути менше 4 автобусів.
4) Математична модель (розв’язок симплекс-методом за допомогою складання симплекс-таблиць) має вигляд:
Z(x) = X1+X2+X3+X4+X5+X6 > min
X1 + X6>=4,
X1 + X2>=8,
X2 + X3>=10,
X3 + X4>=7,
X4 + X5>=12,
X5 + X6>=4,
X1 , X2 , X3 , X4 , X5 , X6 >= 0.
= >
X1 + X6 - X7 = 4,
X1 + X2 - X8 = 8,
X2 + X3 - X9 = 10,
X3 + X4 - X10 = 7,
X4 + X5 - X11 = 12,
X5 + X6 - X12 = 4,
X1 , X2 , X3 , X4 , X5 , X6 ? 0.
Якщо система обмежень містить знак «>», то додається змінна зі знаком «-». Якщо знак «<», то до лівої частини нерівності додається додаткова змінна зі знаком «+».
Додаткові змінні вводять в цільову функцію з нульовим коефіцієнтом: X7, X8, X9, X10, X11, X12.
Виводимо базисні змінні:
X7 = -4 + X1 + X6,
X8 = -8 + X1 + X2,
X9 = -10 + X2 + X3,
X10 = -7 + X3 + X4,
X11 = -12 + X4 + X5,
X12 = -4 + X5 + X6.
Для знаходження початкового опорного рішення будуємо початкову симплекс – таблицю(таблиця 2):
Таблиця 2
| Ci | БП | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | Z(x) |
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | X10 | X11 | X12 | bi | | |
| 0 | X7 | -1 | 0 | 0 | 0 | 0 | -1 | 1 | 0 | 0 | 0 | 0 | 0 | -4 |
| 0 | X8 | -1 | -1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | -8 |
| 0 | X9 | 0 | -1 | -1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | -10 |
| 0 | X10 | 0 | 0 | -1 | -1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | -7 |
| 0 | X11 | 0 | 0 | 0 | -1 | -1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | -12 |
| 0 | X12 | 0 | 0 | 0 | 0 | -1 | -1 | 0 | 0 | 0 | 0 | 0 | 1 | -4 |
| Дj | -1 | -1 | -1 | -1 | -1 | -1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
1 2