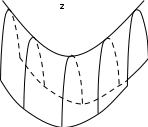
Лекця №10 Параболоїди. Прямолінійні твірні поверхонь 2-го порядку. Загальне рівняння поверхонь 2-го порядку.
Означення. Поверхня, яка утворена в результаті обертання параболи навколо її осі називається параболоїдом обертання.
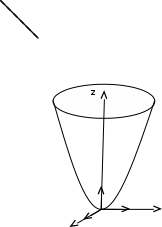
Знайдемо канонічне рівняння параболоїда обертання. Нехай в прямокутній системі координат в площині
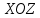задано параболу. 
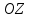– вісь параболи, а 
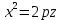(1) – канонічне рівняння параболи. Скористаємося рівнянням обертання навколо осі
: 
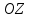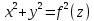(2) тоді 
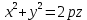, p>0;
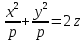, тоді 
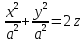(3) – канонічне рівняння параболоїда обертання.Якщо вітки параболи направленні вниз (p<0), то
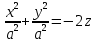.З рівняння (3) слідує:
Поверхня обмежена з одної сторони площиною
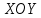;Вісь
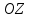є віссю симетрії поверхні (вісь параболоїда обертання);Площини
, 
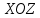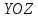є площинами симетрії;Точка перетину осі параболоїда з поверхнею називається вершиною (одна вершина – початок координат).
Розглянемо перерізи параболоїда.
Нехай z=h, тоді
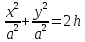. Розглянемо три можливі випадки:Якщо h=0, то
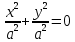- точка (перетин уявних прямих).Якщо h<0, то переріз є порожньою множиною,
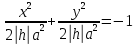– уявний еліпс.Якщо h>0, то
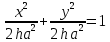– отримаємо коло.Нехай x=h, тоді
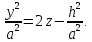Якщо h=0, то 
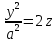– парабола,якщо
; 
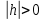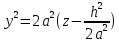.Еліптичний параболоїд.
Означення. Поверхня, яка утворена в результаті стиснення параболоїда обертання до площини, яка проходить через вісь обертання називається еліптичним параболоїдом.
Знайдемо канонічне рівняння еліптичного параболоїда. Виконаємо стиснення простору по OY до площини
(
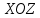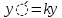). Тоді рівняння параболоїда матиме вигляд: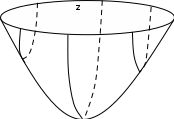
, 
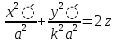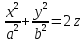– канонічне рівняння еліптичного параболоїда, 
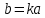.Еліптичний параболоїд можна отримати іншим способом. Розглянемо дві параболи. Одна з них нерухома в
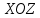, а друга в площині 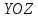– рухома. Будемо рухати рухому параболу так, щоб її вершина весь час лежала на нерухомій параболі, а площини параболи були паралельні площині 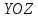. В результаті отримаємо еліптичний параболоїд.Властивості.
Поверхня є обмеженою площиною
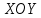.Група симетрій поверхні містить 3 елементи. Вісь
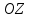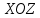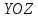і 2 площини симетрії та .Якщо z=h , то можливі випадки:
h>0 – в перерізі отримаємо еліпс;
h=0 – в перерізі точка(вершина);
h<0 – в перерізі отримаємо порожню множину
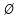.Гіперболічний параболоїд.
Розглянемо дві параболи
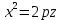і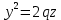 
; q<0, p>0.Нехай парабола, що лежить в
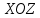нерухома, а в 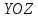- рухома, причому рухається так, що її вершина рухається на параболі 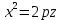і її площина паралельна 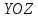.У результаті цього утвориться гіперболічний параболоїд, канонічне рівняння якого
, 
, 
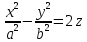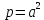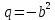.Властивості.
Поверхня необмежена.
Група симетрій складається з трьох елементів: вісь симетрії
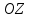і дві площини симетрі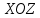ї і 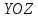.Нехай z=h, тоді матимемо випадки:
h>0 ,
, 
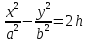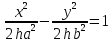, отримаємо гіперболу;h=0,
, 
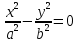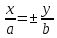, отримаємо дві прямі, що перетинаються;h<0,
, 
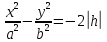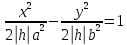, отримаємо гіперболу.Якщо x=h, то отримуємо в перерізі параболу.
Якщо y=h, то також отримуємо в перерізі параболу.
Лекця №11. Прямолінійні твірні поверхні 2-го порядку.
Означення. Прямолінійною твірною поверхні 2-го порядку називається пряма лінія, всі точки якої належать даній поверхні. Із розглянутих вище нами поверхонь прямолінійні твірні мають циліндричні і конічні поверхні (всі їх твірні є прямолінійними твірними), а також однопорожнинний гіперболоїд і гіперболічний параболоїд.
Прямолінійні твірні одно порожнинного гіперболоїда.
Канонічне рівняння однопорожнинного гіперболоїда
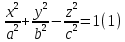.На поверхні (1) розглянемо т.
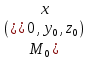Через т. 
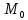проведемо пряму, напрям якої задається вектором 
. Будемо шукати спільні точки поверхні (1) і прямої рівняння якої матиме вигляд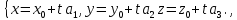 
(2)Підставимо x,y,z з (2) в (1):
, 
,
,
, 
, 
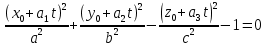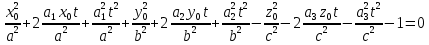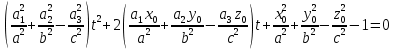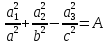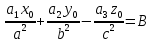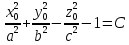, тоді маємо:
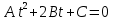(3) . Оскільки пряма (1) повністю лежить на поверхні (2), то(3) повинне виконуватися при будь-якому t . Покладемо в (3) t=0, t=1, t=-1. Отримаємо:Якщо t=0, то c=0,
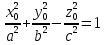(4.1);Якщо t=1, то A+2B=0; (4)
Якщо t=-1, то A-2B=0;
Розв’язавши систему
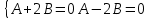отримаємо A=0, B=0. Тоді
; 
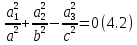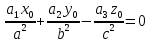(4.3).Отримали умови (4) при яких пряма (2) буде прямолінійною твірною поверхні (1).
Зауваження. Умова(4.1) показує, що т.
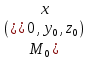повинна належати поверхні (1), а (4.2), (4.3) – умови, які повинні задовольняти координати напрямного вектора 
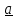прямої (2).Оскільки
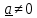, то не зменшуючи загальності вважаємо, що 
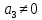. Позначимо 
; 
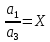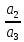=Y . Запишемо (4.2) (4.3) у вигляді:
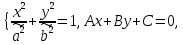(5) 
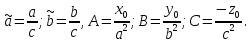
Кожен розв’язок (x,y) системи (5) визначає напрямний вектор прямої (2). Перше рівняння системи визначає еліпс на площині
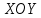, а друге рівняння пряму в цій же площині. Оскільки пряма з еліпсом має не більше двох спільних точок, то через кожну точку 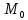поверхні проходить не більше двох прямолінійних твірних поверхні.Рівняння 1 однопорожнинного гіперболоїда представимо у вигляді:
Розглянемо дві системи рівнянь:
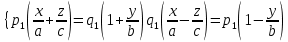(6) 
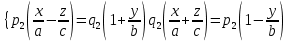(7)де
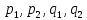– деякі дійсні числа, із яких хоча б одне відмінне від нуля. Очевидно, що в (6) і (7) ранг матриці, складеної із коефіцієнтів при x,y,z рівний 2, отже кожна із систем визначає пряму лінію.Через будь-яку точку поверхні проходить дві прямолінійні твірні, одна належить одному сімейству(6), а друга – сімейству(7). Дві прямолінійні твірні одного сімейства мимобіжні.
Твірні гіперболічного параболоїда.
Нехай в ортонормованому репері R гіперболічний параболоїд задано рівнянням
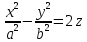(8), а пряма 
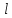задана рівнянням (2). Підставимо (2) в (8):
,
, 
, 
, 
, 
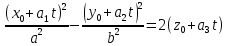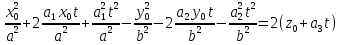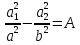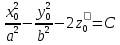, тоді маємо: 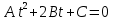.Пряма (2) належить гіперболічному параболоїду (8) , тому записана вище рівність справедлива при будь-яких t.
Якщо t=0, то
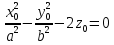(9)Якщо t=1, то A+2B=0;
Якщо t=-1, то
A-2B=0; Розв’язавши систему
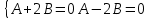отримаємо A=0, B=0. Тоді 
, 
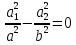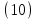
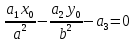
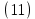.Запишемо рівняння (8) так:
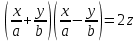.Розглянемо дві системи рівнянь:
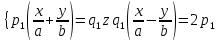(12) і 
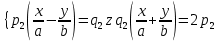(13)
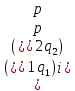– деякі дійсні числа, з кожної пари яких, хоча б одне не було нулем.Кожна із систем (12), (13) визначає пряму лінію. Прямолінійні твірні які належать сімейству (12) паралельні площині bx-ay=0; a(13)- bx+ay=0.
Дві прямолінійні твірні гіперболічного параболоїда, які належать різним сімействам перетинаються, а дві прямолінійні твірні одного сімейства мимобіжні.
Дотична площина до поверхні 2-го порядку