
Ім'я файлу: Лекція Понтрягін.doc
Розширення: doc
Розмір: 229кб.
Дата: 23.04.2020
скачати
Пов'язані файли:
Диплом-зразок.doc
Розширення: doc
Розмір: 229кб.
Дата: 23.04.2020
скачати
Пов'язані файли:
Диплом-зразок.doc
Лекція « Принцип максимуму Л.С. Понтрягіна»
Принцип розроблений Л.С. Понтрягіним та його школою у 1961 р. для розв’язку задач оптимального управління та й досі є актуальним завдяки чіткому та компактному формулюванню основного результату. На противагу класичному варіаційному численню (метод Ейлера, множників Лагранжа, Якобі, Вейєрштраса), де функція оптимального керування шукається в класі неперервних функцій, в принципі максимуму функція керування може належати кусково-неперервним функціям, з точками розриву першого роду або сукупності ізольованих точок. Наприклад, оптимальне керування можна шукати в класі релейних функцій.
Для процесів, що описуються системами нелінійних диференціальних рівнянь принцип максимуму формулюється як необхідна умова оптимальності. Для системи лінійних диференціальних рівнянь принцип максимуму є достатньою умовою оптимальності. Принцип максимуму розповсюджується на процеси з розподіленими параметрами, що описуються рівняннями в частинних похідних.
багатьох задач оптимального керування існує три основні задачі, що розв’язуються за принципом максимуму: задача керування за максимальної швидкодією; задача керування кінцевим станом; задача керування з мінімізацією інтегралу. Саме тому принцип максимуму набув широкого розповсюдження.
Сформулюємо задачу оптимального управління.
Нехай процес описується системою диференціальних рівнянь
(11.1)
де
Передбачено, що вектор управління u може приймати свої значення з деякої множини U. Також передбачається, що функції fi (i=1,2,…,n) неперервні за всіма своїми змінними та неперервно-диференційовані за змінними вектора x . Допустимі управління є кусково-неперервними функціями uv (v=1,2,…m), що задовольняють умові u(t) ∈U .
Векторний простір з декартовими координатами
заданий вектор u(t) та початкові умови
1
відповідати різні розв’язки
x(t)
рівняння , тобто вибором
u(t)
можна
керувати рухом системи. Розв’язку
x(t)
,
t0≤ t ≤ t1,у фазовому просторіХ
відповідає деяка лінія, що називається фазовою траєкторією системи.
Нехай у фазовому просторі Х задані дві точки
керувань
u(t) ,
. Розглянемо наступну задачу. Необхідно серед допустимих
t0≤ t ≤ t1,тобто кусково-неперервних вектор-функцій u(t) ∈U
(моменти
t0, t1
– не фіксовані), що переводять фазову точку системи (3.1) з
заданого початкового положення
| | t1 | | | | (11.2) |
| I = | f0(x1, x2,...,xn,u1,u2,...,um)dt | | |||
| | ∫t0 | | та фазова траєкторія x(t) , що розв’язують дану задачу | ||
| Управління u(t) | |||||
| називаються оптимальними. | | x3 | |||
| | x2 | 1 | | | |
| | | | 0 | ||
| | | | x | | x =(x1(t0),x2(t0),x3(t0)) |
| | | x*(t) =(x1(t1),x2(t1)) | | x*(t) | |
| | | | | | |
| | | | x1 | | |
| x0=(x1(t0),x2(t0 | | x2 | x1 | ||
| а) | x1=(x1(t1),x2(t1),x3(t1)) б) | ||||
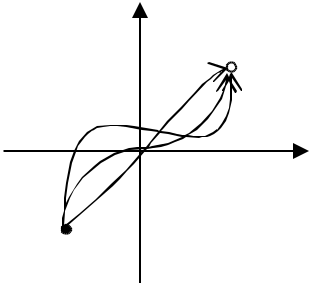
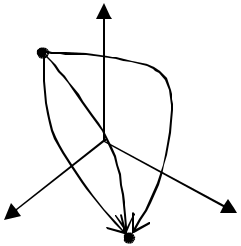
))
Рис.4. Приклади фазових траєкторій: а) n=2; б) n=3.
Принцип максимуму передбачає використання додаткових процедур:
вводиться додаткова штучна змінна стану x0 :
-
dx0
= f0 (x, u),
(11.3)
dt
де: f0 (x,u) відповідає підінтегральному виразу з (11.2);
2
вводяться допоміжні функції ψ 0 ,ψ1....ψ n , ,які визначаються лінійними однорідними рівнянням, що мають єдине рішення:
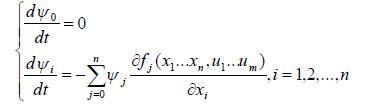
(11.4)
приєднується вираз (11.3) до системи (11.1), що утворює систему з (n+1) рівнянь
-
dxi =f(x,x...x
,u ,u
...u ), i = 0,1,...,n
(11.5)
i 1 2
n 1 2
m
dt
вводиться
(11.6)
допоміжна
функція H
(функція
Гамільтона) у
вигляді
H (ш,x,u)=∑ψj f j(x,u);
j=0
Безпосередньою перевіркою впевнюємося, що рівняння (11.4) може бути переписане:
| | dψ | 0 = 0 | | | | (11.7) | ||||||
| | dt | | | | ||||||||
| | dψ | | | | ∂H (ш, x,u) | ,i = 1,2,...,n | | |||||
| | | i | = − | | | | | |||||
| | | | | ∂x | | | ||||||
| | dt | | | | | | | |||||
| | | | | | i | | | | ||||
| а рівняння (3.1) перепишеться: | | |||||||||||
| | dxi = | | ∂H (ш, x,u) | ,i = 0,1,...,n . | (11.8) | |||||||
| | dt | | | | | ∂ψ i | | | | |||
При фіксованих векторах ш та x функція H (ш, x,u) стає функцією вектора
. Введемо:
M (ш,x)=max H (ш,x,u).
(11.9)
u∈U
Теорема (принцип максимуму Понтрягіна). Нехай, u(t) , t0 ≤ t ≤ t1 –
допустиме управління, а x(t) – відповідна їй траєкторія, що переводить
фазову точку x системи з заданого початкового стану x0 в заданий
кінцевий стан x1 , де . Якщо u(t) та – оптимальні x(t)
керування та траєкторія, то знайдеться така неперервна вектор-функція
= ψ 0 ,ψ 1 ,...,ψ n , яка задовольняє рівнянням , що:
1) в кожен момент часу t, t0≤ t ≤ t1, функція H (ш(t),x(t), u(t)), що
розглядається як функція змінної u , досягає в точці u = u(t)
максимуму
(ш(t), x(t),u(t)) = M (ш(t), x(t)) ; (11.10)
виконана умова не тривіальності розв’язку системи рівнянь (11.7):
3
ш(t) ≠ 0 ;
3) в кінцевий момент часу t1
ψ 0(t1)≤0, M (ш(t1),x(t1))=0.
(11.11)
Максимум неперервної функції
H (ш(t),x(t), u(t))
може досягатися як в
точках локального максимуму цієї функції, в яких частинна перша похідна дорівнює нулю:
-
∂H
= 0, k = 1,2,...,m
(11.12)
∂uk
та друга частинна похідна менша за нуль, так і на границях області U. Отже, центральним моментом в принципі максимуму є вираз
,
(11.13)
який означає, що якщо
- оптимальні керування, а
- оптимальні траєкторії, то знайдуться така постійна
та такі розв’язки
системи (11.7), що
функція H
від
змінних
U саме при оптимальних керуваннях
На початку, вважаючи
на якій досягається найбільше значення функції H.
4
Якщо ця функція відома та ((11.7)-(11.8)):
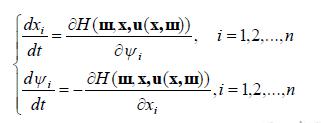
(11.15)
розв’язуючи яку з крайовими умовами
Таким чином, принцип максимуму дозволяє звести розв’язок задачі оптимального програмного керування до розв’язку крайової задачі.
Якщо явний вигляд оптимального керування (11.14) отримати неможливо, то система Гамільтона разом з умовами максимуму (11.12) або створюють крайову задачу принципу максимуму.
Задача на швидкодію.
В задачах на швидкодію критерій оптимальності перепишеться:
-
t1
f 0
=1 I =1dt = t1− t0,
;
∫
t 0
тоді гамільтоніан прийме вигляд:
H (ш,x,u)=ψ0
+ n∑ψ i fi (x,u);
i =1
Введемо n-вимірний вектор ψ1...ψ n та функцію:
n
(ш, x,u) = ∑ψ i fi (x,u);
=1
відповідності з вектор ш задається рівняннями:
dψi= −∂
dt ∂xi
Якщо H (ш(t), x(t),u *(t)) = M (ш(t), x(t)) , то і
(ш(t), x(t),u *(t)) = M (ш(t), x(t)) (3.20)
(11.16)
(11.17)
(11.18)
(11.19)
Теорема (принцип максимуму в задачах на швидкодію). Нехай , u(t ) , t0≤ t ≤ t1–допустиме управління,аx(t)–відповідна їй траєкторія,що
5
переводить фазову точку x системи (11.1) з заданого початкового стану x0 в заданий кінцевий стан x1 . Якщо u(t) та x(t) – оптимальні керування та траєкторія за швидкодією, то знайдеться така неперервна вектор-функція
-
ш = (ψ1 (t),ψ 2 (t),...,ψ n (t)) , яка задовольняє рівнянням що:
1) в кожен момент часу t, t0 ≤ t ≤ t1 , функція
(ш(t), x(t),u) , що
H
розглядається як функція змінної u , досягає
в точці u = u(t)
максимуму
(ш(t), x(t),u(t)) =
(ш(t), x(t)) ;(11.21)
H
M
виконана умова не тривіальності розв’язку системи рівнянь (11.19):
ш(t) ≠ 0 ;
в кінцевий момент часу t1
-
(ш(t1 ), x(t1)) ≥ 0 .
(11.22)
M
Як у випадку попередньої теореми, якщо виконано співвідношення (11.21) та (11.22) ((11.7) та (11.9)), то функція M (ш(t), x(t)) ( M (ш(t), x(t )) ) на оптимальній траєкторії постійна. Тому, співвідношення (11.22) ((11.10)) можна
перевіряти на всьому проміжку t ∈ [t0 ,t1].
теоремі принципу максимуму передбачається, що вектор ш(t) визначається з точністю до постійного додатного множника, тому завжди можна покласти ш(t0 ) = 1 .
Необхідною умовою мінімуму функціоналу є умова Вейєрштраса, яку можна записати у вигляді:
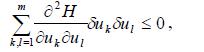
(11.23)
де uk (k=1,2,…m)–нескінченно мала варіація оптимального керування.
Приклад.
Записати крайову задачу принципу максимуму для кожухотрубного теплообмінника, що описується системою диференціальних рівнянь у відхиленнях (знак D - опущено):
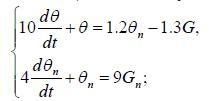
(11.24)
де перше рівняння описує ємність нагріваємої рідини, а друге – ємність теплоносія (пари); θ – температура рідини; θп – температура пари; G – витрата рідини; Gп – витрата пари, що надходить в міжтрубний простір; t – час. Оптимальне керування, обмежене виразами
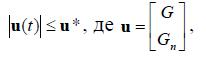 (11.25)
(11.25)6
повинно переводити об’єкт з початкового стану x0 в кінцевий x1 за мінімальний час.
Розв’язання.
Приводимо об’єкт до безрозмірної форми:
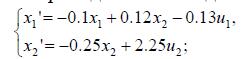 (11.26)
(11.26)Складаємо функцію Гамільтона:
n
H (ш,x,u)=∑ψi fi(x,u)=ψ1(−0.1x1+0.12x2−0.13u1)+ψ2(−0.25x2+2.25u2)(11.27)
i=1
Оптимальне керування має вигляд:
-
u1(t)= u1* sign(−0.13ψ1(t));
u2(t)= u2* sign(2.25ψ2(t)).
(11.28)
4. Складаємо систему спряжених рівнянь за (11.19):
ψ'1=0.1ψ 1,
(11.29)
ψ '= −0.12ψ
2
1 + 0.25ψ 2.
Отже, отримуємо доточкову крайову задачу (2n+r-рівнянь):
x ' (t)= −0.1x (t)+0.12x (t)−0.13u (t),
x (t )= x0
,
1
1
2
1
1
0
1
x2 '(t ) = −0.25x2
(t) + 2.25u2 (t),
x2(t0)= x02
,
u (t)= u * sign(−0.13ψ(t)),
(11.30)
1
1
1
u2(t)= u2* sign(2.25ψ2(t)),
x (t )= x1,
ψ '1
(t) = 0.1ψ 1 (t),
1
1
1
ψ '2(t)= −0.12ψ 1(t)+0.25ψ 2(t),
x 2(t
1
,2
1) = x
7
розв’язавши яку визначаються оптимальна траєкторія х(t) та функції ψ 1 (t) та
2 (t) , які підставляють у рівняння оптимального керування (11.28).
Відмітимо, якщо початковий вектор х0 не визначений, то крайову задачу доповнюють умовою:
-
ш(t0 ) = 0.
(11.31)
8