Лекція 2: Молекулярно-кінетичні властивості колоїдних систем

Ім'я файлу: Lec_2.docx
Розширення: docx
Розмір: 225кб.
Дата: 10.05.2021
скачати
Пов'язані файли:
курсова транспортування.docx
pidruchnik.doc
Варіанти ДЗ ТТКМ.docx

Лекція 2: Молекулярно-кінетичні властивості колоїдних систем.

Мета: У даній лекції ставиться мета навчити студентів аналітично оцінювати поведінку дисперсних систем під впливом температури (броунівський рух, дифузія), розраховувати осмотичний тиск ультрамікрогетерогенних систем, а також проводити седиментаційний аналіз полідисперсних порошків.
План
Вступ

Броунівський рух у колоїдних розчинах. Рівняння Енштейна.

Дифузія. Осмос.

Седиментація. Седиментаційний-дифузійна рівновага.

Седиментаційний аналіз Висновки Контрольні запитання

Вступ
Молекулярно-кінетична теорія вивчає закони спонтанного руху молекул. Деякі властивості розчинів зумовлені цим рухом, тобто визначаються не хімічним складом, а числом молекул в одиниці об'єму або маси. До таких колігативних властивотей розчинів належать: осмотичний тиск, дифузія, зміна температури їх замерзання або кипіння та ін. У даній лекції ми з^’ ясуємо чи характерні ці властивості для дисперсних систем, об'єкти яких займають проміжне положення між нерухомими крупними тілами і вічно рухомими молекулами.
Зміст лекції

Броунівський рух у колоїдних розчинах. Рівняння Енштейна.

Тепловий рух частинок дисперсної фази в колоїдних і мікрогетерогенних
системах називається броунівським на честь англійського ботаніка Р. Броуна. У 1827 році Броун, спостерігаючи під мікроскопом водну суспензію квіткового пилу, помітив, що частинки пилку перебувають у стані безперервного хаотичного руху. Він не зміг пояснити природу цьго явища, але з'ясував, що рух частинок не ослаблюється з часом. Він тим інтенсивніший, чим вища температура. Експериментальні дослідження броунівського руху привели до

висновку, що він має молекулярно-кінетичну природу, тобто виникає внаслідок зіткнення молекул середовища з частинками дисперсної фази. Внаслідок великого числа ударів частинка змінює напрямок руху дуже часто до 10²⁰ разів за секунду. Тому траєкторія її руху є ламаною лінією, невизначеної конфігурації (рис. 1).

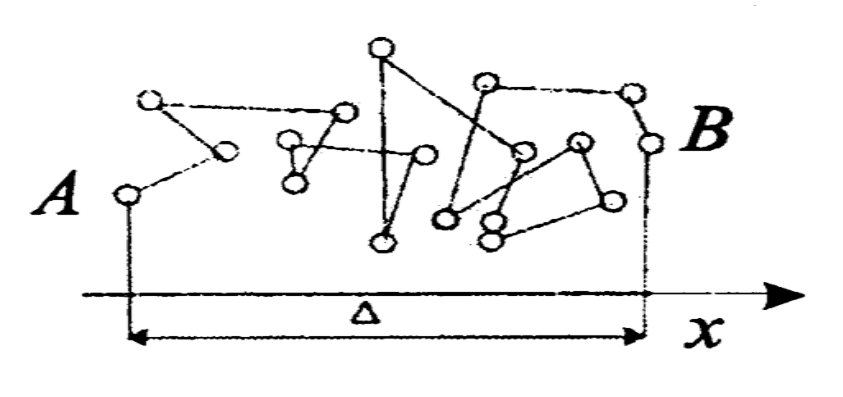
Рис.1. Броунівський рух частинки
Кількісною характеристикою броунівського руху є середній зсув частинки

за час t. Зсувом називають відстань між проекціями початкової (А) і кінцевої (В) точок траєкторії на вісь зміщень (х). Зміщення однаково ймовір ні як зліва на право, так і в протилежному напрямку, тому обчислюють середню квадратичну

величину.

∆
		∆∆∆⋯∆	(1)
			(1)
де ∆₁, ∆₂, ∆₃ –	окрім проекції зміщення частинок на вісь х; n – кількість

таких проекцій. Для сферичн ої частинки з радіусом r величина середнього зсуву

пропорційна

абсолютній

температурі

Т, часу

спостереження t і

обернено

пропорційна коефіцієнту тертя B 6πηr

:

∆

( 2)

Для коефіцієнта пропорційності b теорія Енштейна дає вираз:

b

2k

, оскільки k

.

1.38 ∙ 10

ДжК ^-1]

.∙

∆

(3 )

∆

∙

або

Т

(4)

де k —

константа Больцмана, η —

в'язкість середовища.

Із рівняння Енштейна-Смолуховського (3) видно, що ∆ зменшується при

зростанні радіуса. При розмірі r > 5000 нм (> 5мкм) броунівський рух припиняється.
Виміряні і розраховані значення ∆ співпадають і це є доказом систематичного характеру другого закону термодинаміки: S = kInW до W — термодинамічна ймовірність стану системи, S — ентропія, k – стала Больцмана.

Дифузія. Осмос.

Дифузія — це самочинний процес вирівнювання концентрації частинок в об'ємі системи рідини або газу під впливом теплового руху. Цей процес веде

також до вирівнювання в				об'ємі системи хімічного потенціалу.
Кількісно дифузія				описується рівнянням Фіка:
			−			(5),
			−			(5),
де dm –	маса речовини, що продифундувала за час dt; D —						коефіцієнт
дифузії; dc/dx	— градієнт концентрації; S — площа перерізу,						через який

відбувається дифузія. Знак мінус показує, що дифузія йде в бік зменшення концентрації. Якщо –dc/dx =1, S=1, dt =1, то D=dm, тобто коефіцієнт дифузії дорівнює масі речовини, що продифондувала в одиницю часу, через одиницю площі, при градієнті концентрації рівному одиниці. Розмірність D — [ м²с^-1]
Енштейн вивів рівняння (6), яке зв'язує коефіцієнт дифузії D з температурою Т, в'язкістю дисперсійного середовища η і радіусом частинок дисперсійної фази r:
(6)

Із рівняння (6) випливає, що коефіцієнт дифузії обернено пропорційний радіусу частинок. У зв'язку з цим у колоїдно-дисперсних системах, частинки яких значно більші за молекули, спостерігається повільна дифузія.

Співставляючи рівняння∆√2(3) та (6) одержуємо:

(7)
Рівняння (7) використовується для визначення коефіцієнту дифузії D, а при відомому значенні D рівняння (6) дозволяє визначити розмір частинок r.
Явище осмосу обумовлене дифузією. Поняття осмосу для розчинів полягає в тому, що в посудині, розділеної напівпроникною мембраною, яка пропускає тільки молекули розчинника, розчинник із меншою концентрацією розчиненої речовини буде переходити в об'єм із більшою концентрацією розчиненої речовини.
Аналізуючи результати досліджень Вант-Гофф дійшов висновку, що розчинена речовина в слабкому розчині веде себе так ніби вона є в газоподібному стані при цих же умовах. Він використовує рівняння стану

ідеальних газів для розчинів:
П			(8),

де П — осмотичний тиск, V —			об'єм розбавленого розчину, n — кількість
молів розчиненої речовини.

Рівняння (8) записують у вигляді:
П	(9),

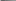
де С — концентрація розчиненої речовини, моль/л. Для одномолярного розчину любої речовини при 273К р = 2.27 10⁶ Па.
Для дисперсних систем

П ∙ (10) ,

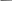
де m - маса дисперсної фази, m₀ - маса частинки, V - об'єм дисперсії, ν - частинкова концентрація, К - стала Больцмана.
Кількість частинок у золях на 5-7 порядків менша за кількість атомів в розчинах, тому величина П низька.

організмі людини кров, лімфа та інші тканеві рідини організму мають осмотичний тиск 8·10⁵ Па. Такий же тиск має 0,9 % розчин NaCl. Цей розчин називають фізіологічним.

Седиментація. Седиментаційний-дифузійна рівновага.

дисперсних системах, у яких відсутня здатність до хаотичного руху частинок, внаслідок дії поля тяжіння, будуть поступово осідати, поки повністю не випадуть в осад.

Процеси осідання частинок дисперсної фази під дією сили тяжіння називають седиментацією, а системи в яких йдуть ці процеси, називають кінетично нестійкими.
Дисперсні системи, в яких для частинок дисперсійної фази характерний хаотичний (броунівський) рух є більш чи менш кінетично стійкими. Осіданню частинок завжди протидіє броунівський рух, який прагне рівномірно розподілити частинки по всьому об`єму системи. Чим менші частинки, тим сильніше виявляється броунівський рух і дифузія. Внаслідок броунівського руху, з одного боку, і дії сили тяжіння, з другого боку, встановлюється седиментаційно-дисперсійна рівновага, яка характеризується певним рівноважним розподілом частинок за висотою.

мікрогетерогенних системах позбавлених броунівського руху частинки дисперсної фази осідають або спливають (якщо ρ < ρ₀).

Умовою рівномірного руху частинок при осадженні є рівність сили тяжіння, опору і виштовхуючої сили Архімеда:

F_тяж=F_оп+F_вишт (11)
Для середньої частинки радіусу r і масою m, яка рухається з постійною
швидкістю осадження (седиментації) u_сед, із врахуванням закону Стокса можна записати

− 6πrηu сед (12),

де ρ і ρ₀ — густини дисперсної фази і дисперсного середовища.
На сферичну частинку із радіусом r і густиною ρ, що вільно осідає в дисперсійному середовищі, густина якого ρ₀ і в'язкість η, діє комплексна сила,

^Fтяж ^{— F} вишт ^:

тяж— вишт							( −				)			(13)

Сила опору середовища:
F_оп = 6πrηu_сед														(14)
У деякий момент сили тяжіння урівноважуються силами тертя і частинка
рухається з постійною швидкістю:
		πr g(ρ − ρ ) 6									сед			(15)

Звідси:				сед			(	)						(16)

Отже швидкість сферичної частинки, яка вільно рухається, під впливом сили тяжіння, прямо пропорційна квадрату її радіуса і обернено пропорційна в’язкості дисперсного середовища.
Швидкість руху частинки можна знайти із відношення пройденого

шляху h до часу t і підставити їх у рівняння (16) і знайти радіус частинки:

		(		~~⁄ )~~						(17)
	(			)
У данному					рівнянні величина							− стала для даної

									(	)

системи і умов досліду, тоді:

(18)

Рівняння (18) вірне для частинок із радіусом r =10^-7÷10 ^-4м. Для прискорення осадження частинок дисперсних систем А.Р.Думанский запропонував використовувати центрифугу, тобто замінити гравітаційні сили тяжіння на відцентрове гравітаційне поле. Пізніше шведський вчений Т.Сведберг сконструював ультрацентрифугу. У сучасних ультрацентрифугах

кількість обертів досягає декілька десятків тисяч у секунду, а відцентрове прискорення — мільйонів g.
Радіус частинок за швидкістю осадження в ультрацентрифузі визначають за рівнянням:

(

)

)

(

⁄

(19),

де ω — кутова швидкість; х₁, х₂ - відстань чвстинок від осі обертання на

початку досліду і через проміжок часу τ.

У

наведеному рівнянні

(

⁄

)

-

постійна величина і її називають константою седиментації:

Sосад. ln

⁄ω

⋅ τ

(20)

Для сферичних частинок осідаючих у гравітаційному полі

сед.

(

)

сед.

(21)

Величина зворотня

седиментації

є

мірою кінетичної

стійкості

дисперсної системи:

(22 )

сед.

сед.

Оскільки більшість реальних дисперсних систем мають частинки неправильної форми, то за рівняннями (19), (17) можна розрахувати так званий еквівалентний радіус, тобто радіус частинки сферичної форми, яка осідає з такою ж швидкістю.
На практиці дисперсну систему характеризують розподілом і фракціями.
Даний аналіз одержав назву седиментаційного аналізу.
Реальні дисперсні системи є полідисперсними і тому крупні частинки осідають швидше, малі — повільніше.
В ультромікрогетерогенних системах (золях) через певний час після їх приготування швидкості дифузійних і седиментаційних потоків вирівнюється і наступає седиментаційна рівновага. Цю рівновагу можна записати

універсальним законом розподілу Больцмана:
e			(23),

де ν₀ - концентрація частинок в вихідному			стані; ν- концентрація

частинок на висоті h з потенціальною енергією U. Остання величина з

врахуванням виштовхуючоїℎ сили Архімеда визначається за рівнянням:

(24)

Рівняння (24) підставляємо в (23) і після логарифмування отримуємо рівняння Лапласа – Перрене:

( )( )

(25)

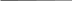
Рівняння (25) є окремим випадком універсального закону розподілу Больцмана, за допомогою якого вперше вдалося знайти константу молекулярно-кінетичної теорії — число Авогадро.

Седиментаційний аналіз

На практиці дисперсну систему характеризують розподілом
частинок за розмірами і фракціями (вміст дисперсної фази в заданих інтервалах радіусів частинок). Такий аналіз полідисперності одержав назву седиментаційного аналізу.
Він передбачає одержання кривої седиментації, тобто залежності маси осаду m дисперсної фази, яка осіла до певного часу, від часу осадження t. Для монодисперсної системи (з частинками одного розміру) така залежність є лінійною:
(26),

де – загальна маса дисперсної фази; Н – початкова висота стовпа дисперсної системи.
Усі реальні дисперсні системи полідисперсні (частинки дисперсної фази мають різні розміри), і тому швидкість осідання різна для різних фракцій: крупні частинки осідають швидше, малі — повільніше. Тому крива седиментації вигнута до осі ординат.
Тангенси кута нахилу дотичних в даних точках кривої седиментації
визначають швидкості седиментації відповідних фракцій частинок. Знаючи швидкість осадження частинок окремих фракцій, за рівнянням (19) можна розрахувати їх розміри (радіуси). Загальна кількість дисперсної фази, яка осіла до довільного моменту часу t₁, виразиться рівняння:

+		(27)

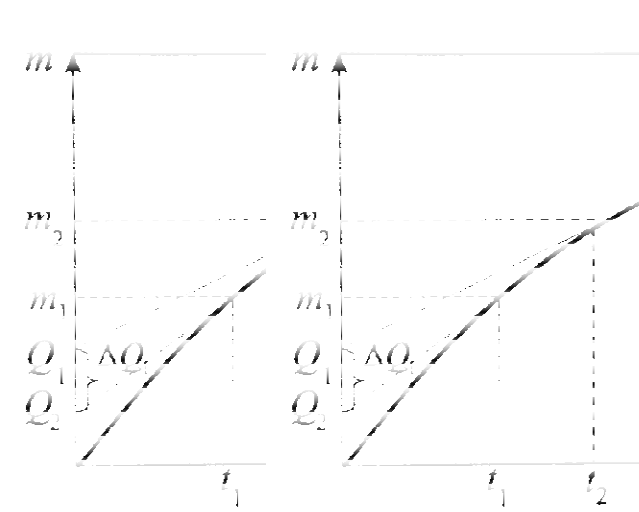
Рис. 2. Крива седиментації полідисперсної системи

Величина визначається відрізком, який відсікається на осі ординат дотичною до кривої седиментації в точці t₁, і характеризує ма су частинок

фракції, які повністю ви пали в осад до моменту часу t₁. Оскільки радіус частинок, які пройшли за ч ас t₁, усю висоту стовпа Н дисперсної системи,

, то

—

це маса частинок системи з

. Член

(

)

характеризує масу частинок

, які осіли до моменту часу

t₁.

Як правило, визначають відносну масу частинок дисперс ної фази, які

осіли (в %

від загального

вмісту дисперсної фази в систем і). В цьому

випадку m_найб = 100%, а величини

,

є процентними вмістами фракцій

з

радіусом

відповідно

,

і

так далі. Таким чином,

можна

збудувати інтегральну криву розподілу частинок за їх ро змірами — залежність % від r. Загал ьний вигляд кривої зображений на рис. 3.
Інтегральна крива дозволяє визначити процентний вміст фракцій.

Наприклад, для фракції, яка містить частинки розміром від r до r , маса фракції дорівнює ∆ − . 1 2

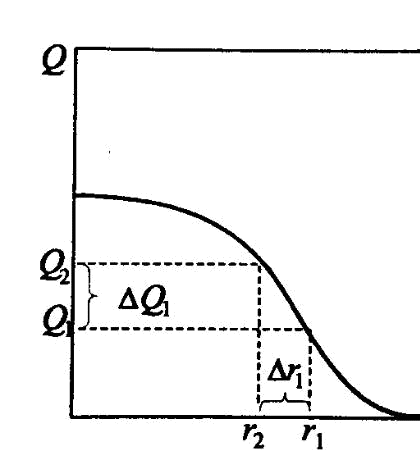
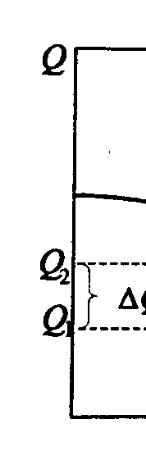
Рис. 3. Інтегральна крива розподілу частинок за радіусом
Більш наочну уяву про р озподіл частинок в дисперсній системі за

розмірами дає диференціальна крива розподілу, яка є залежністю ∆/∆ (в межі / ) від радіусу частинок r (рис. 4)

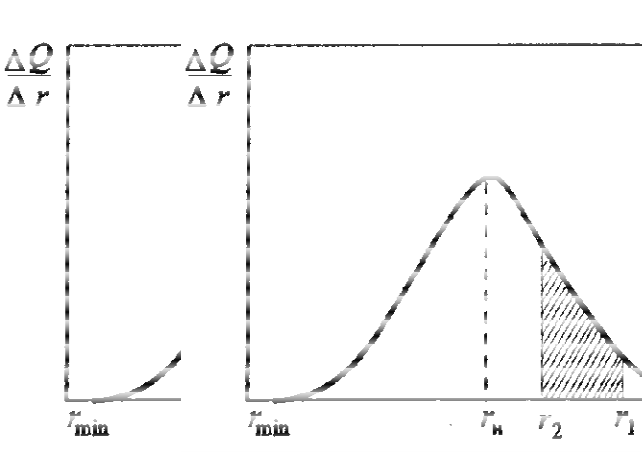
Рис. 4. Диференціальна крива розподілу частинок за радіусом

Для її побудови можна використати інтегральну криву, визначаючи збільшення ∆ для серії фракцій ∆r, або криву седиментації (рис. 2),
визначаючи ∆ як відрізки, що відсікаються сусідніми дотичними на осі ординат, наприклад, ∆ − . Для знаходження ∆r = r2 – r 1 н еобхідно
визначити радіус частинок, які осіли до моменту часу t₁ і t₂. Максимум на диференціальній кривій відповідає найбільш характерному для системи радіусу частинок. Щоб знайти за кривою розподілу процентний вміст частинок з
радіусом від r₁ до r₂, треба взяти відношення площі, заштрихованої на рисунку, до площі під усією кривою і помножити на 100.

Для проведення седиментаційного аналізу полідисперсних си стем використовують різного виду седиментометри (Рис. 5).

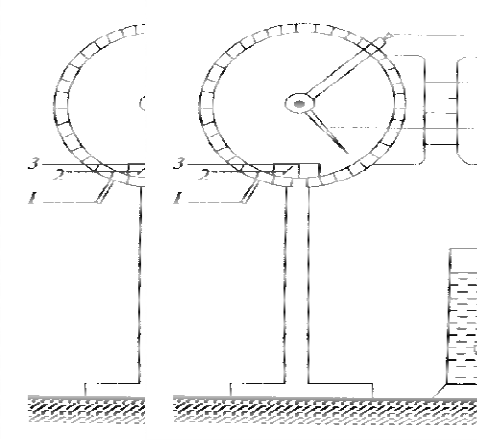
Рис. 5. Схема проведення седиментаційного аналізу з використанням торсійної ваги: 1 – аретир; 2 – риска; 3 – циферблат; 4 – важіль урівноваження; 5 – стрілка ваги; 6 – гачок для шальки; 7 – скляний циліндр

При аналізі високодиспперсних систем або систем з малою різницею густини частинок дисперсної фази і дисперсійного середовища седиментацію проводять у гравітаційному полі з використанням центрифуги.
Висновки

Таким чином, коротки й розгляд молекулярно-кінетичних властивостей дисперсних систем пок азує, що високодисперсні (ультрамікрогетерогенні) системи принципово не відрізняються від молекулярних розчині в. їх властивості описуються загальним и закономірностями, але виражені значно слабкіше, внаслідок малих величин частинкової концентрації.

Властивості ж низькодисперсних (мікрогетерогенних) систем значно відрізняються від властивостей молекулярних розчинів: частинки цих систем нездатні до хаотичного теплового руху, в них не відбуваються дифузія і осмос.

Контрольні питання

Яка природа броунівського руху і якою величиною він кількісно характеризується?

Чому броунівський рух не відбувається у мікрогетерогенних системах?

Як теорія броунівського руху підтвердила реальність існування молекул?

В чому полягає фізичний зміст коефіцієнта дифузії?

Які особливості осмотичного тиску ліозолів? Як він залежить від дисперсності?

Чому осмометрію не використовують для визначення розмірів колоїдних частинок?

7.Що таке седиментаційно-дифузійна рівновага? Як можна в її умовах визначити розміри частинок?

В чому полягає седиментаційний аналіз монодисперсної системи? Полідисперсної системи?

Як за допомогою диференціальної кривої розподілу частинок за радіусами визначити вміст окремої фракції?

10.Яким чином завдяки ультрацентрифузі можна проаналізувати високодисперсні системи?
скачати

© Усі права захищені
написати до нас