
Ім'я файлу: 1.docx
Розширення: docx
Розмір: 784кб.
Дата: 18.11.2020
скачати
Пов'язані файли:
Язиката Хвеська_сценарій.doc
Маковійчук есе Тип особистості.docx
аналітична записка.docx
9 веселих ігор для дітей.docx
Внесок Л.С. Виготського в дитячу психологію.doc
Реферат по Трудовому.docx
1 ЛАБА.docx
Розширення: docx
Розмір: 784кб.
Дата: 18.11.2020
скачати
Пов'язані файли:
Язиката Хвеська_сценарій.doc
Маковійчук есе Тип особистості.docx
аналітична записка.docx
9 веселих ігор для дітей.docx
Внесок Л.С. Виготського в дитячу психологію.doc
Реферат по Трудовому.docx
1 ЛАБА.docx
ТЕМА 1. ВСТУП. ДІЙСНІ ЧИСЛА
ЛЕКЦІЯ 1
Вступ.
Пончття множини. Дії з множинами.
1. Вступ
Математичний аналіз – частина математики, в якій функції і їх узагальнення вивчаються методами границь. Поняття границі тісно пов'язане з поняттям нескінченно малої величини, тому можна також сказати, що математичний аналіз вивчає функції та їх узагальнення методом нескінченно малих.
"Математичний аналіз" є скороченою назвою старої назви цієї частини математики – "Аналіз нескінченно малих". У класичному математичному аналізі об'єктами вивчення (аналізу) є перш за все функції. Розвиток математичного аналізу привів до можливості вивчення його методами більш складних утворень, ніж функція, функціоналів, операторів і т. д.
У природі та техніці зустрічаються зміни, рухи, які є першою ознакою того, що ми називаємо явищем, процесом. Закони явищ природи зазвичай описуються функціями. Звідси об'єктивна важливість математичного аналізу як засобу вивчення функцій .
Математичний аналіз у широкому розумінні цього терміна охоплює дуже велику частину математики. До нього входять диференціальне числення, інтегральне числення, теорія функцій дійсної змінної, теорія функцій комплексної змінної, наближення функцій, теорія диференціальних рівнянь, теорія інтегральних рівнянь, диференціальна геометрія, варіаційне числення, функціональний аналіз і деякі інші математичні науки.
Усе ж термін "математичний аналіз" часто застосовується для найменування лише основ математичного аналізу, які об'єднують у собі теорію дійсного числа, теорію границь, теорію рядів, диференціальне й інтегральне числення і їх безпосередні застосування, такі, як теорія максимумів та мінімумів, теорія неявних функцій, ряди Фур'є, інтеграли Фур'є.
2. Пончття множини. Дії з множинами
Поняття множини. Поняття множини є первісним поняттям, тобто таким, якому не дається означення. Можна говорити про множину N усіх натуральних чисел, множину Z усіх цілих чисел, множину Q усіх раціональних чисел і т. д. Творець теорії множин Георг Кантор (1845-1919) розумів множину як зібрання певних та різних об'єктів нашої інтуїції або інтелекту, які сприймаються в якості цілого.
Множина вважається визначеною, якщо про будь-який об'єкт, що розглядається, можна сказати, що він належить або не належить цій множині. Якщо деякий елемент X належить множині A, то пишуть 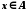 . Якщо елемент X не належить множині A, то це записують так:
. Якщо елемент X не належить множині A, то це записують так:  .
.
Нехай X– деяка фіксована множина (іноді її називають основною) і P– певна властивість, яку мають деякі елементи 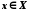 . Множина всіх елементів
. Множина всіх елементів  , що належать множині X і мають властивість P, позначається таким чином:
, що належать множині X і мають властивість P, позначається таким чином:
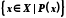 або
або 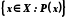 .
.
Наприклад, якщо в значенні основної множини взяти множину Z, то множина 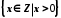 є множиною натуральних чисел.
є множиною натуральних чисел.
Якщо множина має скінченне число елементів, то її можна задати переліком її елементів, тобто записати  .
.
Множина, яка не містить жодного елемента, називається порожньою і позначається знаком  .
.
Дії з множинами. Множина А називається підмножиною множини В, якщо кожний елемент множини А є елементом множини В, тобто якщо 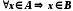 . Якщо множина
. Якщо множина 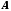 є підмножиною множини В, то пишуть
є підмножиною множини В, то пишуть 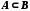 або
або 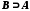 .
.
Для будь-якої множини А приймається, що 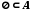 .
.
Множини А та В називаються рівними, якщо 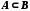 і
і 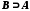 . Рівність множин позначається так: А=В.
. Рівність множин позначається так: А=В.
Об'єднанням (сумою) множин А та В називається множина С, яка складається з елементів, кожен із яких належить множині А або множині В. Об'єднання множин позначається так: 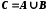 .
.
Перерізом (добутком) множин А і В називається множина С, яка складається з елементів, кожен із яких належить як множині А, так і множині 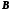 . Записується:
. Записується: 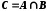 .
.
Різницею множин А і В називається множина С, яка складається з усіх тих елементів множини А, які не належать множині В. Різниця множин позначається так: 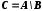 .
.
Нехай Х − основна множина і 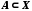 . Доповненням до множини А називається множина
. Доповненням до множини А називається множина 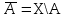 .
.
Правила двоїстості. Для будь-яких множин А і В мають місце співвідношення:
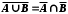 ;
;
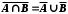 .
.
Доведемо перше із співвідношень.
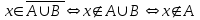 ,
, 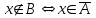 ,
,
 .
.
Отже, 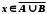
 , тобто
, тобто 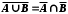 .
.
Аналогічно доводиться друге співвідношення.
Частково впорядковані множини. Нехай М − довільна множина і 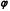 − деяке бінарне відношення в ній. Це відношення називається частковою впорядкованістю, якщо воно задовольняє умови:
− деяке бінарне відношення в ній. Це відношення називається частковою впорядкованістю, якщо воно задовольняє умови:
1) рефлексивності: 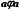 ;
;
2) транзитивності: якщо 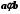 і
і 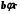 , то
, то 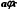 ;
;
3) антисиметричності: якщо 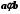 і
і 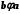 , то
, то  .
.
Часткова впорядкованість може позначатися символом 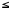 . Множина, в якій задано деяку часткову впорядкованість, називається частково впорядкованою. Запис
. Множина, в якій задано деяку часткову впорядкованість, називається частково впорядкованою. Запис 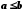 означає, що елемент а не перевищує b або що він підпорядкований b, передує b, а b − не менше від а йде за а.
означає, що елемент а не перевищує b або що він підпорядкований b, передує b, а b − не менше від а йде за а.
У випадку, коли 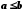 та
та 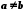 , користуються символом < , тобто пишуть
, користуються символом < , тобто пишуть 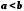 і говорять, що а менше від b або що а строго підпорядковане b.
і говорять, що а менше від b або що а строго підпорядковане b.
Частково впорядкована множина, для будь-яких двох точок а, b якої існує точка c, що йде за ними (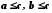 ), називається напрямленою.
), називається напрямленою.
Приклади.
1. Множина всіх натуральних чисел частково впорядкована, якщо 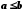 означає „b ділиться на a без остачі”.
означає „b ділиться на a без остачі”.
2. Множина всіх підмножин деякої фіксованої множини частково впорядкована за включенням, якщо 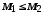 означає, що
означає, що 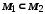 .
.
3. Упорядкованою парою (a , b) є множина 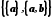 .
.
Нехай a, b − елементи частково впорядкованої множини. Може виявитися, що жодне із співвідношень 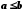 і
і 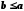 не має місця. У цьому випадку елементи a, b називаються непорівнянними. Тобто відношення порядку може бути визначеним лише для деяких пар елементів, тому й говориться про часткову впорядкованість. Якщо ж в частково впорядкованій множині M непорівняних елементів немає, то множина M називається впорядкованою ( лінійно впорядкованою, цілком упорядкованою ).
не має місця. У цьому випадку елементи a, b називаються непорівнянними. Тобто відношення порядку може бути визначеним лише для деяких пар елементів, тому й говориться про часткову впорядкованість. Якщо ж в частково впорядкованій множині M непорівняних елементів немає, то множина M називається впорядкованою ( лінійно впорядкованою, цілком упорядкованою ).
Декартовим добутком множин 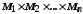 називається множина впорядкованих
називається множина впорядкованих  -ок:
-ок:
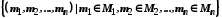 .
.
Застосовується позначення 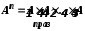 .
.
ЛЕКЦІЯ 2
Загальне поняття відображення або функції.
Потужність множини.
Зчисленні множини.
Математична індукція.
1. Загальне поняття відображення або функції
Нехай X і Y дві множини. Відображенням f множини X у множину Y називається правило, яке кожному елементу 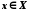 ставить у відповідність один і тільки один елемент
ставить у відповідність один і тільки один елемент 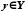 .
.
Замість слова "відображення" можна вживати "функція", "оператор", "відповідність".
Записи 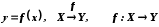 означають, що f є відображенням множини X у множину Y.
означають, що f є відображенням множини X у множину Y.
Для позначення функції вживаються й інші букви, наприклад 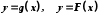 .
.
Елемент y, який відображення f ставить у відповідність елементу  , називається образом елемента
, називається образом елемента  при відображенні f або значенням відображення f у точці
при відображенні f або значенням відображення f у точці  і позначається символом
і позначається символом 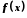 . Множина X називається областю визначення відображення f і позначається
. Множина X називається областю визначення відображення f і позначається 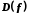 . Множина
. Множина 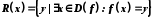 називається множиною значень відображення f.
називається множиною значень відображення f.
Нехай 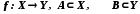 . Образом множини A при відображенні f називається множина
. Образом множини A при відображенні f називається множина 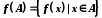 . Прообразом множини
. Прообразом множини 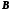 при відображенні
при відображенні 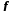 називається множина
називається множина 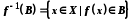 .
.
Графіком функції 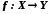 називається множина
називається множина 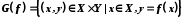 .
.
Якщо 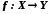 і
і 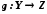 , то функція
, то функція 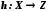 , яка визначається формулами
, яка визначається формулами 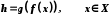 називається складеною функцією, або суперпозицією функцій f і g.
називається складеною функцією, або суперпозицією функцій f і g.
Приклади.
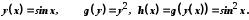
Відображення 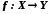 називається відображенням множини Х на множину
називається відображенням множини Х на множину 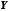 або сур'єкцією, якщо
або сур'єкцією, якщо 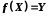 .
.
Відображення 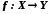 називається взаємооднозначним відображенням множини X у множину Y або ін'єкцією, якщо
називається взаємооднозначним відображенням множини X у множину Y або ін'єкцією, якщо
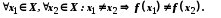
Відображення 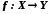 , яке є сур'єкцією та ін'єкцією, називається бієкцією. У цьому випадку говорять, що
, яке є сур'єкцією та ін'єкцією, називається бієкцією. У цьому випадку говорять, що 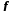 здійснює взаємно однозначну відповідність між множинами
здійснює взаємно однозначну відповідність між множинами  і
і 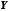 .
.
Якщо 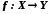 − бієкція, то
− бієкція, то 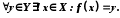 Функція
Функція 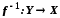 називається оберненою до бієкції
називається оберненою до бієкції 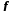 , якщо
, якщо 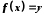 та
та 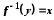 .
.
Відображення 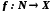 називається послідовністю елементів із
називається послідовністю елементів із  . Послідовність позначається так:
. Послідовність позначається так: 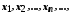 де
де 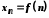 −
−  -ний член послідовності.
-ний член послідовності.
2. Потужність множини
Множина, яка складається із скінченного числа елементів, називається скінченною. Для скінченної множини 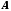 число її елементів позначається
число її елементів позначається 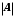 . Скінченні множини можна порівнювати за кількістю їх елементів. Виникає питання, як можна порівнювати нескінченні множини? Г. Кантор побудував теорію, яка містить відповідь на поставлене питання. Вихідним пунктом цієї теорії є поняття потужності множини.
. Скінченні множини можна порівнювати за кількістю їх елементів. Виникає питання, як можна порівнювати нескінченні множини? Г. Кантор побудував теорію, яка містить відповідь на поставлене питання. Вихідним пунктом цієї теорії є поняття потужності множини.
Множини 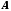 і
і 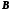 називаються рівнопотужними (мають однакову потужність), якщо існує бієкція
називаються рівнопотужними (мають однакову потужність), якщо існує бієкція 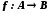 . Рівнопотужні множини позначають так: A
. Рівнопотужні множини позначають так: A
B.
3. Зчисленні множини
Множина 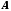 називається зчисленною, якщо A
називається зчисленною, якщо A
N. У цьому випадку говорять, що елементи множини ТЕМА 1. ВСТУП. ДІЙСНІ ЧИСЛА
ЛЕКЦІЯ 1
Вступ.
Пончття множини. Дії з множинами.
1. Вступ
Математичний аналіз – частина математики, в якій функції і їх узагальнення вивчаються методами границь. Поняття границі тісно пов'язане з поняттям нескінченно малої величини, тому можна також сказати, що математичний аналіз вивчає функції та їх узагальнення методом нескінченно малих.
"Математичний аналіз" є скороченою назвою старої назви цієї частини математики – "Аналіз нескінченно малих". У класичному математичному аналізі об'єктами вивчення (аналізу) є перш за все функції. Розвиток математичного аналізу привів до можливості вивчення його методами більш складних утворень, ніж функція, функціоналів, операторів і т. д.
У природі та техніці зустрічаються зміни, рухи, які є першою ознакою того, що ми називаємо явищем, процесом. Закони явищ природи зазвичай описуються функціями. Звідси об'єктивна важливість математичного аналізу як засобу вивчення функцій .
Математичний аналіз у широкому розумінні цього терміна охоплює дуже велику частину математики. До нього входять диференціальне числення, інтегральне числення, теорія функцій дійсної змінної, теорія функцій комплексної змінної, наближення функцій, теорія диференціальних рівнянь, теорія інтегральних рівнянь, диференціальна геометрія, варіаційне числення, функціональний аналіз і деякі інші математичні науки.
Усе ж термін "математичний аналіз" часто застосовується для найменування лише основ математичного аналізу, які об'єднують у собі теорію дійсного числа, теорію границь, теорію рядів, диференціальне й інтегральне числення і їх безпосередні застосування, такі, як теорія максимумів та мінімумів, теорія неявних функцій, ряди Фур'є, інтеграли Фур'є.
2. Пончття множини. Дії з множинами
Поняття множини. Поняття множини є первісним поняттям, тобто таким, якому не дається означення. Можна говорити про множину N усіх натуральних чисел, множину Z усіх цілих чисел, множину Q усіх раціональних чисел і т. д. Творець теорії множин Георг Кантор (1845-1919) розумів множину як зібрання певних та різних об'єктів нашої інтуїції або інтелекту, які сприймаються в якості цілого.
Множина вважається визначеною, якщо про будь-який об'єкт, що розглядається, можна сказати, що він належить або не належить цій множині. Якщо деякий елемент X належить множині A, то пишуть
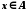 . Якщо елемент X не належить множині A, то це записують так:
. Якщо елемент X не належить множині A, то це записують так:  .
.Нехай X– деяка фіксована множина (іноді її називають основною) і P– певна властивість, яку мають деякі елементи
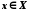 . Множина всіх елементів
. Множина всіх елементів  , що належать множині X і мають властивість P, позначається таким чином:
, що належать множині X і мають властивість P, позначається таким чином: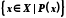 або
або 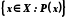 .
.Наприклад, якщо в значенні основної множини взяти множину Z, то множина
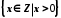 є множиною натуральних чисел.
є множиною натуральних чисел.Якщо множина має скінченне число елементів, то її можна задати переліком її елементів, тобто записати
 .
.Множина, яка не містить жодного елемента, називається порожньою і позначається знаком
 .
.Дії з множинами. Множина А називається підмножиною множини В, якщо кожний елемент множини А є елементом множини В, тобто якщо
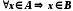 . Якщо множина
. Якщо множина 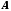 є підмножиною множини В, то пишуть
є підмножиною множини В, то пишуть 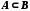 або
або 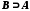 .
.Для будь-якої множини А приймається, що
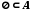 .
.Множини А та В називаються рівними, якщо
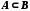 і
і 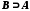 . Рівність множин позначається так: А=В.
. Рівність множин позначається так: А=В.Об'єднанням (сумою) множин А та В називається множина С, яка складається з елементів, кожен із яких належить множині А або множині В. Об'єднання множин позначається так:
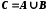 .
.Перерізом (добутком) множин А і В називається множина С, яка складається з елементів, кожен із яких належить як множині А, так і множині
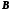 . Записується:
. Записується: 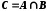 .
.Різницею множин А і В називається множина С, яка складається з усіх тих елементів множини А, які не належать множині В. Різниця множин позначається так:
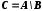 .
.Нехай Х − основна множина і
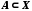 . Доповненням до множини А називається множина
. Доповненням до множини А називається множина 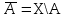 .
.Правила двоїстості. Для будь-яких множин А і В мають місце співвідношення:
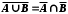 ;
;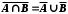 .
.Доведемо перше із співвідношень.
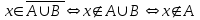 ,
, 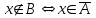 ,
, .
.Отже,
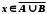
 , тобто
, тобто 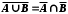 .
.Аналогічно доводиться друге співвідношення.
Частково впорядковані множини. Нехай М − довільна множина і
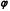 − деяке бінарне відношення в ній. Це відношення називається частковою впорядкованістю, якщо воно задовольняє умови:
− деяке бінарне відношення в ній. Це відношення називається частковою впорядкованістю, якщо воно задовольняє умови:1) рефлексивності:
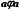 ;
;2) транзитивності: якщо
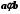 і
і 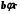 , то
, то 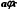 ;
; 3) антисиметричності: якщо
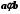 і
і 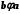 , то
, то  .
.Часткова впорядкованість може позначатися символом
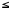 . Множина, в якій задано деяку часткову впорядкованість, називається частково впорядкованою. Запис
. Множина, в якій задано деяку часткову впорядкованість, називається частково впорядкованою. Запис 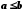 означає, що елемент а не перевищує b або що він підпорядкований b, передує b, а b − не менше від а йде за а.
означає, що елемент а не перевищує b або що він підпорядкований b, передує b, а b − не менше від а йде за а.У випадку, коли
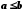 та
та 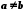 , користуються символом < , тобто пишуть
, користуються символом < , тобто пишуть 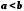 і говорять, що а менше від b або що а строго підпорядковане b.
і говорять, що а менше від b або що а строго підпорядковане b.Частково впорядкована множина, для будь-яких двох точок а, b якої існує точка c, що йде за ними (
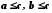 ), називається напрямленою.
), називається напрямленою.Приклади.
1. Множина всіх натуральних чисел частково впорядкована, якщо
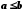 означає „b ділиться на a без остачі”.
означає „b ділиться на a без остачі”.2. Множина всіх підмножин деякої фіксованої множини частково впорядкована за включенням, якщо
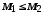 означає, що
означає, що 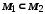 .
.3. Упорядкованою парою (a , b) є множина
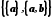 .
.Нехай a, b − елементи частково впорядкованої множини. Може виявитися, що жодне із співвідношень
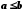 і
і 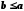 не має місця. У цьому випадку елементи a, b називаються непорівнянними. Тобто відношення порядку може бути визначеним лише для деяких пар елементів, тому й говориться про часткову впорядкованість. Якщо ж в частково впорядкованій множині M непорівняних елементів немає, то множина M називається впорядкованою ( лінійно впорядкованою, цілком упорядкованою ).
не має місця. У цьому випадку елементи a, b називаються непорівнянними. Тобто відношення порядку може бути визначеним лише для деяких пар елементів, тому й говориться про часткову впорядкованість. Якщо ж в частково впорядкованій множині M непорівняних елементів немає, то множина M називається впорядкованою ( лінійно впорядкованою, цілком упорядкованою ).Декартовим добутком множин
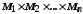 називається множина впорядкованих
називається множина впорядкованих  -ок:
-ок: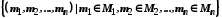 .
.Застосовується позначення
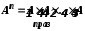 .
.ЛЕКЦІЯ 2
Загальне поняття відображення або функції.
Потужність множини.
Зчисленні множини.
Математична індукція.
1. Загальне поняття відображення або функції
Нехай X і Y дві множини. Відображенням f множини X у множину Y називається правило, яке кожному елементу
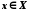 ставить у відповідність один і тільки один елемент
ставить у відповідність один і тільки один елемент 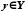 .
.Замість слова "відображення" можна вживати "функція", "оператор", "відповідність".
Записи
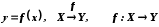 означають, що f є відображенням множини X у множину Y.
означають, що f є відображенням множини X у множину Y.Для позначення функції вживаються й інші букви, наприклад
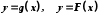 .
.Елемент y, який відображення f ставить у відповідність елементу
 , називається образом елемента
, називається образом елемента  при відображенні f або значенням відображення f у точці
при відображенні f або значенням відображення f у точці  і позначається символом
і позначається символом 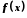 . Множина X називається областю визначення відображення f і позначається
. Множина X називається областю визначення відображення f і позначається 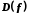 . Множина
. Множина 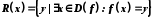 називається множиною значень відображення f.
називається множиною значень відображення f.Нехай
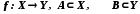 . Образом множини A при відображенні f називається множина
. Образом множини A при відображенні f називається множина 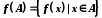 . Прообразом множини
. Прообразом множини 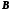 при відображенні
при відображенні 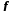 називається множина
називається множина 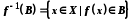 .
.Графіком функції
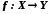 називається множина
називається множина 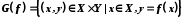 .
.Якщо
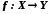 і
і 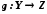 , то функція
, то функція 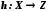 , яка визначається формулами
, яка визначається формулами 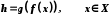 називається складеною функцією, або суперпозицією функцій f і g.
називається складеною функцією, або суперпозицією функцій f і g.Приклади.
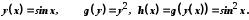
Відображення
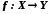 називається відображенням множини Х на множину
називається відображенням множини Х на множину 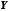 або сур'єкцією, якщо
або сур'єкцією, якщо 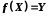 .
.Відображення
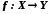 називається взаємооднозначним відображенням множини X у множину Y або ін'єкцією, якщо
називається взаємооднозначним відображенням множини X у множину Y або ін'єкцією, якщо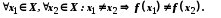
Відображення
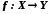 , яке є сур'єкцією та ін'єкцією, називається бієкцією. У цьому випадку говорять, що
, яке є сур'єкцією та ін'єкцією, називається бієкцією. У цьому випадку говорять, що 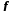 здійснює взаємно однозначну відповідність між множинами
здійснює взаємно однозначну відповідність між множинами  і
і 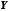 .
.Якщо
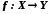 − бієкція, то
− бієкція, то 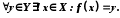 Функція
Функція 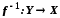 називається оберненою до бієкції
називається оберненою до бієкції 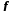 , якщо
, якщо 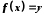 та
та 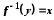 .
.Відображення
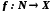 називається послідовністю елементів із
називається послідовністю елементів із  . Послідовність позначається так:
. Послідовність позначається так: 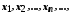 де
де 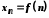 −
−  -ний член послідовності.
-ний член послідовності.2. Потужність множини
Множина, яка складається із скінченного числа елементів, називається скінченною. Для скінченної множини
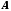 число її елементів позначається
число її елементів позначається 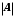 . Скінченні множини можна порівнювати за кількістю їх елементів. Виникає питання, як можна порівнювати нескінченні множини? Г. Кантор побудував теорію, яка містить відповідь на поставлене питання. Вихідним пунктом цієї теорії є поняття потужності множини.
. Скінченні множини можна порівнювати за кількістю їх елементів. Виникає питання, як можна порівнювати нескінченні множини? Г. Кантор побудував теорію, яка містить відповідь на поставлене питання. Вихідним пунктом цієї теорії є поняття потужності множини.Множини
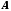 і
і 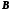 називаються рівнопотужними (мають однакову потужність), якщо існує бієкція
називаються рівнопотужними (мають однакову потужність), якщо існує бієкція 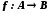 . Рівнопотужні множини позначають так: A
. Рівнопотужні множини позначають так: A 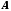 можна занумерувати.
можна занумерувати.Мають місце наступні твердження:
Нескінченна підмножина зчисленної множини зчисленна.
Нескінченна множина містить зчисленну підмножину.
Об'єднання зчисленної множини зчисленних множин є зчисленною множиною.
Декартів добуток двох зчисленних множин зчисленний.
Існують незчисленні множини.
Доведення першого і другого твердження досить прості. Їх пропонується виконати самостійно. Спинимось на доведенні твердження 3.
Нехай
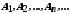 - зчисленні множини. Тоді для кожного
- зчисленні множини. Тоді для кожного 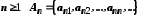 .
.Елементи об'єднання
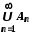 цих множин можна подати у вигляді таблиці
цих множин можна подати у вигляді таблиці
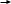
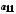
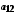
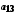 …
… 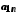 …
…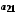
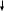
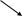
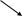
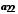
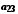 …
… 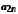 …
…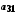
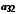
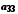 …
… 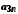 …
……………………………………………
і занумерувати, наприклад у порядку, вказаному стрілками. Цим саме буде встановлена бієкція
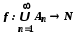 . Отже,
. Отже, 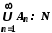 .
.Аналогічно доводиться твердження 4.
Нехай
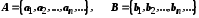 . Тоді декартів добуток
. Тоді декартів добуток 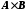 складається із пар, які можна розташувати в такому порядку
складається із пар, які можна розташувати в такому порядку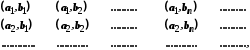
і занумерувати так, як зроблено в попередньому випадку.
Для доведення твердження 5 застосуємо діагональний метод (діагональну процедуру) Кантора.
Нехай
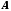 − множина всіх можливих нескінченних ланцюгів, що складаються з двох символів, наприклад 0 і 1, вигляду
− множина всіх можливих нескінченних ланцюгів, що складаються з двох символів, наприклад 0 і 1, вигляду 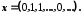
Покажемо, що множина
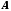 незчисленна. Припустимо, що елементи множини
незчисленна. Припустимо, що елементи множини 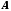 занумеровані, тобто що множина
занумеровані, тобто що множина 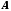 зчисленна. Нехай
зчисленна. Нехай 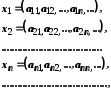
де кожне
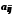 дорівнює 0 або 1. Утворимо елемент
дорівнює 0 або 1. Утворимо елемент 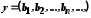 , поклавши
, поклавши 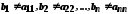 , і кожне
, і кожне 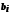 відповідно дорівнює 0 або 1. Очевидно, що
відповідно дорівнює 0 або 1. Очевидно, що 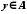 , але не збігається з жодним із занумерованих елементів
, але не збігається з жодним із занумерованих елементів 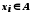 . А це суперечить тому, що всі елементи множини
. А це суперечить тому, що всі елементи множини 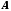 можна занумерувати.
можна занумерувати.4. Математична індукція
Математична індукція - це метод доведення математичних тверджень, який полягає у наступному: твердження
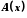 , яке залежить від натурального параметра
, яке залежить від натурального параметра  , вважається доведеним, якщо доведено
, вважається доведеним, якщо доведено 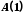 і
і 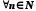 із припущення, що справедливе
із припущення, що справедливе 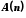 , доведено справедливість
, доведено справедливість 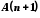 .
.Доведення твердження
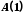 називається першим кроком індукції (базисом індукції), а доведення
називається першим кроком індукції (базисом індукції), а доведення 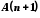 за припущення справедливості
за припущення справедливості 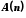 називається індуктивним переходом. При цьому
називається індуктивним переходом. При цьому  називається параметром індукції, а припущення
називається параметром індукції, а припущення 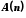 при доведенні
при доведенні 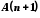 називається індуктивним припущенням.
називається індуктивним припущенням.Нехай
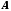 – зчисленна множина і для nÎN
– зчисленна множина і для nÎN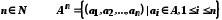
є множина впорядкованих n-членних ланцюгів. Тоді за твердженням 4 і методом (принципом) математичної індукції
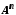 є зчисленною множиною
є зчисленною множиною 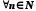 .
.ЛЕКЦІЯ 3
Дійсні числа.
Деякі властивості дійсних чисел.
1. Дійсні числа
Уведемо аксіоматичне означення дійсних чисел.Із шкільного курсу математики відомо, що множина дійсних чисел складається із множини раціональних та ірраціональних чисел. Раціональним називається число, яке можна подати у вигляді звичайного дробу
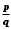 , де p,q− цілі числа, причому
, де p,q− цілі числа, причому 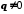 . Ірраціональним називається число, яке не є раціональним. Будь-яке раціональне число є або цілим, або скінченним чи нескінченним періодичним десятковим дробом. Ірраціональні числа – це нескінченні періодичні десяткові дроби. Виявлення ірраціональних чисел пов'язане з установленням у школі Піфагора (570-496 р. до н. е.) несумірності діагоналі квадрата і його сторони, тобто з установленням того факту, що довжина діагоналі квадрата не може бути виражена раціональним числом, якщо в значенні одиниці вимірювання взяти довжину сторони квадрата.
. Ірраціональним називається число, яке не є раціональним. Будь-яке раціональне число є або цілим, або скінченним чи нескінченним періодичним десятковим дробом. Ірраціональні числа – це нескінченні періодичні десяткові дроби. Виявлення ірраціональних чисел пов'язане з установленням у школі Піфагора (570-496 р. до н. е.) несумірності діагоналі квадрата і його сторони, тобто з установленням того факту, що довжина діагоналі квадрата не може бути виражена раціональним числом, якщо в значенні одиниці вимірювання взяти довжину сторони квадрата.Ми дамо аксіоматичне означення множини дійсних чисел.
Множиною дійсних чисел називається множина елементів, для яких виконуються наступні аксіоми.
1. Аксіоми додавання і множення
Для будь-якої пари
 та
та 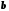 дійсних чисел однозначно виражене число
дійсних чисел однозначно виражене число 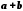 , яке називається їх сумою.
, яке називається їх сумою.Для будь-якої пари
 і
і 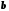 дійсних чисел однозначно виражене число
дійсних чисел однозначно виражене число 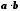 , яке називається їх добутком.
, яке називається їх добутком.Для будь-яких дійсних чисел a,b,c виконуються наступні аксіоми:

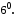 Існує єдине число 0, таке, що
Існує єдине число 0, таке, що 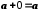 для будь-якого числа
для будь-якого числа  .
.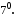 Для будь-якого числа
Для будь-якого числа  існує таке число
існує таке число 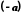 , що
, що  (число
(число 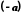 називається протилежним числу
називається протилежним числу  ).
).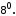 Існує єдине число 1, таке, що
Існує єдине число 1, таке, що 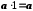 для будь-якого числа
для будь-якого числа  .
.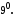 Для будь-якого числа
Для будь-якого числа 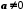 існує таке число
існує таке число 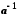 , що
, що 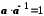 ; число
; число 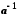 позначається також символом
позначається також символом 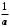 і називається оберненим до
і називається оберненим до  .
.2. Аксіоми порівняння дійсних чисел
Для будь-яких дійсних чисел a,bустановлене одне із співвідношень:
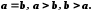
Відношення "=" має властивість: якщо
 і
і 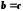 , то
, то 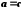 .
.Для будь-яких дійсних чисел a,b,c виконуються наступні аксіоми:
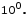 Якщо
Якщо 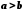 і
і 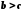 , то
, то 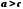 .
.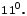 Якщо
Якщо 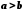 , то
, то 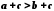 .
.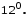 Якщо
Якщо 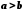 і
і 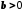 , то
, то  .
.Зауваження. Замість
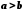 пишуть
пишуть 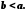
3. Аксіома неперервності дійсних чисел
 Нехай
Нехай  і
і 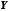 - дві множини, які складаються із дійсних чисел. Тоді, якщо
- дві множини, які складаються із дійсних чисел. Тоді, якщо 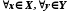 , виконується нерівність
, виконується нерівність  , то існує принаймні одне дійсне число
, то існує принаймні одне дійсне число 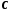 , для якого виконується нерівність
, для якого виконується нерівність 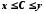 .
.Зауваження. У множині лише раціональних чисел аксіома неперервності не виконується. Дійсно, нехай
 складається із множини раціональних чисел, таких, що
складається із множини раціональних чисел, таких, що 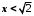 , а
, а 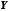 − із множини раціональних чисел
− із множини раціональних чисел 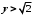 . Тоді
. Тоді 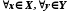 виконується нерівність
виконується нерівність  . Проте не існує раціонального числа
. Проте не існує раціонального числа 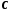 , такого, щоб
, такого, щоб 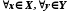 виконувалася б нерівність
виконувалася б нерівність 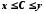 . Таким числом могло бути лише число
. Таким числом могло бути лише число 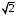 , а воно, як відомо, ірраціональне.
, а воно, як відомо, ірраціональне.2. Деякі властивості дійсних чисел
Наведемо деякі властивості дійсних чисел.
Число
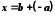 є розв'язком рівняння
є розв'язком рівняння 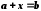 .
.Доведення. Підставимо в дане рівняння замість
 його значення:
його значення: 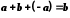 .
.Згідно з
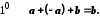
Згідно з

Згідно з
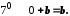
Згідно з
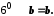
Зауваження. Число
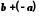 називається різницею чисел
називається різницею чисел  та
та 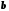 і позначається
і позначається 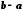 . Зазначимо, що за умови
. Зазначимо, що за умови 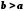 різниця
різниця 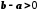 . Дійсно, якщо
. Дійсно, якщо 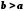 , то за
, то за 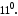 Одержуємо
Одержуємо 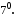 Маємо
Маємо 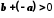 , тобто
, тобто 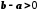 .
.Число
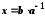 є розв'язком рівняння
є розв'язком рівняння 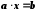 , якщо
, якщо 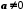 .
.Доведення. Підставимо в дане рівняння значення
 :
: 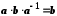 .
.Згідно з
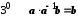 .
.Згідно з
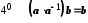 .
.Згідно з
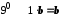 .
.Згідно з
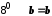 .
.Зауваження. Число
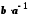 називається часткою чисел
називається часткою чисел  й
й 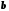 і позначається
і позначається 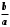 або
або 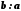 .
.Якщо
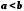 , то
, то 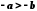 .
.Дійсно, оскільки
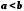 , то
, то 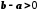 . Отже, за
. Отже, за 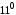
 , звідки одержуємо
, звідки одержуємо 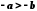 .
.Зокрема, якщо
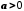 , то
, то 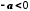 , а якщо
, а якщо 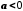 , то
, то  .
.Дійсно, згідно з
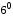
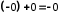 , далі за
, далі за 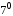
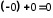 . Отже,
. Отже, 0= − 0.
Якщо
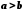 і
і 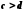 , то
, то 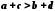 .
.Дійсно, якщо
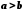 і
і 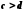 , то за
, то за 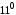
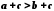 ,
, 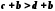 . Далі згідно з
. Далі згідно з 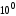
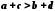 .
.5. Якщо
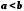 та
та 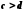 , то
, то 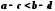 .
.Дійсно, якщо
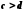 , то згідно з
, то згідно з 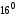
 і за 4 одержуємо:
і за 4 одержуємо: 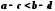 .
.6.
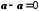 .
.Це випливає з того, що
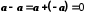 .
.7.
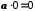 .
.Справді,
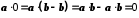 .
. .
.Дана рівність доводиться так:
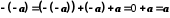 .
.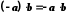 .
.Доведення:
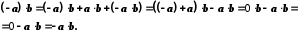
Зокрема,
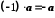 .
.Якщо
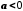 і
і 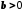 , то
, то 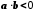 .
.Дійсно, оскільки
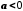 , то
, то  , а тому
, а тому 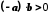 (згідно з
(згідно з  ). Отже,
). Отже, 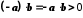 , а звідси
, а звідси 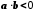 .
.Якщо
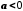 та
та 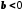 , то
, то  .
.Справді, оскільки
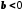 , то
, то 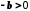 , а тому
, а тому 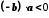 (згідно з
(згідно з 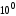 ). Отже,
). Отже, 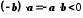 , а звідси маємо
, а звідси маємо  .
.Якщо
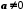 , то
, то 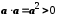 .
.Це випливає з
 і 11.
і 11.За властивістю
 маємо:
маємо: 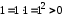 , тобто
, тобто 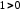 .
.Надалі будемо використовувати й інші властивості дійсних чисел, не спиняючись на їх формальному доведенні.
Із означення множини дійсних чисел випливає, що ця множина впорядкована.
Множину дійсних чисел позначатимемо буквою
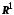 .
.ПИТАННЯ ДЛЯ САМОСТІЙНОГО ОПРАЦЮВАННЯ
Поняття ізоморфізму.
Інтерпретація множини дійсних чисел.
Найбільш вживані числові множини.
Межі числових множин.
Абсолютна величина числа.
1. Поняття ізоморфізму
Нехай задані дві множини об'єктів
 і
і 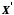 , причому в першій визначені деякі відношення
, причому в першій визначені деякі відношення 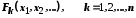 між її об'єктами, а в другій – відношення
між її об'єктами, а в другій – відношення 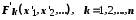 між відповідно своїми об'єктами.
між відповідно своїми об'єктами.Множини
 і
і 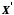 з указаними на них відношеннях називаються ізоморфними (позначається
з указаними на них відношеннях називаються ізоморфними (позначається 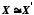 ), якщо між ними встановлено бієктивне відображення
), якщо між ними встановлено бієктивне відображення 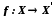 , при якому з наявності відношення
, при якому з наявності відношення 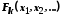 випливає відношення
випливає відношення 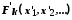 , де
, де 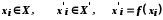 .
.Будь-яку множину об'єктів
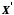 , ізоморфну множині
, ізоморфну множині  , можна розглядати як "модель" множини
, можна розглядати як "модель" множини  і зводити вивчення властивостей множини
і зводити вивчення властивостей множини  до вивчення властивостей "моделі"
до вивчення властивостей "моделі" 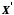 .
.Нехай
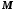 і
і 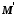 − дві частково впорядковані множини і нехай
− дві частково впорядковані множини і нехай 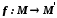 . Якщо з умови
. Якщо з умови 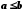 , де
, де 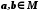 , випливає нерівність
, випливає нерівність 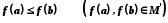 , то говорять, що відображення
, то говорять, що відображення 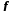 зберігає порядок.
зберігає порядок.Відображення
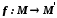 є ізоморфізмом частково впорядкованих множин
є ізоморфізмом частково впорядкованих множин 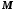 та
та 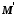 , якщо воно бiєктивне, а співвідношення
, якщо воно бiєктивне, а співвідношення  справджується тоді й тільки тоді, коли
справджується тоді й тільки тоді, коли 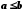 . Самі множини
. Самі множини 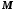 і
і 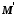 при цьому ізоморфні.
при цьому ізоморфні.2. Інтерпретація множини дійсних чисел
Розглянемо пряму з фіксованою точкою
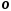 − початком координат. Нехай задана одиниця виміру. Тоді множину дійсних чисел можна поставити у взаємно однозначну відповідність із точками прямої: точці
− початком координат. Нехай задана одиниця виміру. Тоді множину дійсних чисел можна поставити у взаємно однозначну відповідність із точками прямої: точці 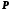 , яка лежить справа від точки
, яка лежить справа від точки 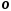 , поставимо у відповідність число
, поставимо у відповідність число 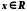 , рівне довжині відрізка
, рівне довжині відрізка 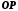 . Тоді
. Тоді 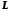 , яка лежить зліва від точки
, яка лежить зліва від точки 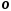 , число
, число 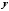 , де
, де 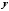 – довжина відрізка
– довжина відрізка 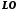 , а точці
, а точці 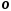 – число 0. Число
– число 0. Число  , яке відповідає точці
, яке відповідає точці 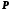 , називається координатою точки
, називається координатою точки 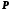 . Пряма з описаними властивостями називається числовою прямою. Отже, кожній точці числової прямої відповідає дійсне число – її координата. Має місце й обернене твердження: кожному дійсному числові
. Пряма з описаними властивостями називається числовою прямою. Отже, кожній точці числової прямої відповідає дійсне число – її координата. Має місце й обернене твердження: кожному дійсному числові  відповідає деяка точка числової прямої, а саме точка
відповідає деяка точка числової прямої, а саме точка 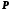 , координата якої
, координата якої  . При так установленій відповідності між дійсними числами і точками прямої нерівність
. При так установленій відповідності між дійсними числами і точками прямої нерівність 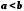 рівносильна тому, що точка з координатою
рівносильна тому, що точка з координатою  лежить зліва від точки з координатою
лежить зліва від точки з координатою 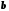 . Отже, можна говорити про ізоморфізм множини дійсних чисел і множини точок числової прямої, тобто що числова пряма є моделлю множини дійсних чисел.
. Отже, можна говорити про ізоморфізм множини дійсних чисел і множини точок числової прямої, тобто що числова пряма є моделлю множини дійсних чисел.Надалі, говорячи про дійсні числа, замість слова "число" іноді вживається слово "точка". У зв'язку з цим числові множини ще називають точковими.
Використовуючи аксіому неперервності множини дійсних чисел, можна встановити, що множина дійсних чисел, яка задовольняє умову
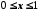 , є незчисленною. Говорять, що ця множина має потужність континууму. Із цього випливає, що множина всіх дійсних чисел незчисленна. Можна також довести, що множина раціональних чисел зчисленна. Отже, множина ірраціональних чисел незчисленна, оскільки вона є множиною
, є незчисленною. Говорять, що ця множина має потужність континууму. Із цього випливає, що множина всіх дійсних чисел незчисленна. Можна також довести, що множина раціональних чисел зчисленна. Отже, множина ірраціональних чисел незчисленна, оскільки вона є множиною 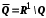 (якби множина
(якби множина 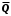 ірраціональних чисел була зчисленною, то і множина
ірраціональних чисел була зчисленною, то і множина 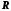 була б зчисленною, оскільки
була б зчисленною, оскільки  ).
).3. Найбільш вживані числові множини
Нехай
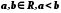 . Будемо використовувати наступні позначення:
. Будемо використовувати наступні позначення: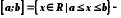 відрізок,
відрізок,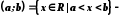 інтервал,
інтервал,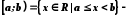 півінтервал,
півінтервал,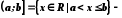 півінтервал.
півінтервал.Указані множини ще називають проміжками. Ми розглядатимемо також і нескінченні множини, використовуючи для цього символи
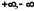 .
.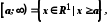

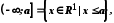
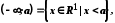
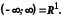
Околом точки
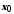 називається довільний інтервал
називається довільний інтервал 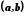 , який містить точку
, який містить точку 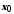 , тобто
, тобто 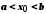 .
.Інтервал
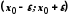 називається
називається 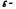 околом точки
околом точки 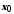 . Точка
. Точка 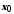 називається центром цього околу, а число
називається центром цього околу, а число 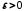 його радіусом. Зазвичай так позначають околи з центром у точці
його радіусом. Зазвичай так позначають околи з центром у точці 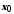 і дуже малим радіусом, тобто коли
і дуже малим радіусом, тобто коли  досить мале.
досить мале.4. Межі числових множин
Нехай задано непорожню числову множину
 .
.Множина
 називається обмеженою зверху, якщо існує таке дійсне число
називається обмеженою зверху, якщо існує таке дійсне число 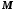 , що для кожного
, що для кожного 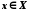 виконується нерівність
виконується нерівність 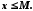
Множина
 називається обмеженою знизу, якщо існує таке дійсне число
називається обмеженою знизу, якщо існує таке дійсне число 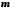 , що для кожного
, що для кожного 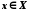 виконується нерівність
виконується нерівність 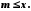
При цьому числа
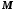 і
і 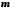 називаються відповідно верхньою та нижньою межею множини
називаються відповідно верхньою та нижньою межею множини .
.Множина, яка обмежена зверху й знизу, називається обмеженою.
Очевидно, що будь-яка обмежена зверху (знизу) множина
 має безліч верхніх (нижніх) меж.
має безліч верхніх (нижніх) меж.Найменша верхня межа обмеженої зверху множини
 називається точною верхньою межею або верхньою гранню цієї множини і позначається
називається точною верхньою межею або верхньою гранню цієї множини і позначається 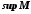 (supremum (лат.) – найвище).
(supremum (лат.) – найвище).Найбільша нижня межа обмеженої знизу множини
 називається точною нижньою межею або нижньою гранню цієї множини і позначається
називається точною нижньою межею або нижньою гранню цієї множини і позначається 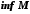 (infimum (лат.) – найнижче).
(infimum (лат.) – найнижче).Якщо
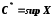 , то для довільного числа
, то для довільного числа 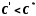 існує
існує 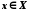 таке, що
таке, що 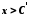 . Якщо
. Якщо 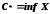 , то для довільного числа
, то для довільного числа 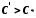 існує
існує 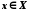 таке, що
таке, що 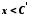 .
. Теорема. Будь-яка непорожня обмежена зверху числова множина має точну верхню межу. Якщо ж вона обмежена знизу, то має точну нижню межу.
Доведення. Нехай
 – непорожня обмежена зверху числова множина. Тоді множина
– непорожня обмежена зверху числова множина. Тоді множина 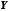 чисел, які обмежують
чисел, які обмежують  зверху, непорожня. Із означення верхньої межі випливає, що
зверху, непорожня. Із означення верхньої межі випливає, що 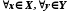 виконується нерівність
виконується нерівність  . За аксіомою неперервності дійсних чисел існує таке число
. За аксіомою неперервності дійсних чисел існує таке число 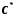 , що
, що 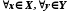 виконується нерівність
виконується нерівність 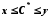 .
.Із цієї нерівності випливає, що
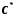 обмежує
обмежує  зверху, тобто є верхньою межею, і є найменшим із усіх верхніх меж, тобто є точною верхньою межею.
зверху, тобто є верхньою межею, і є найменшим із усіх верхніх меж, тобто є точною верхньою межею.Друга частина теореми доводиться аналогічно.
Якщо множина
 не обмежена зверху ( знизу ), то за домовленістю пишуть
не обмежена зверху ( знизу ), то за домовленістю пишуть 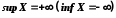 .
.5. Абсолютна величина числа
Абсолютноювеличиною (модулем) числа
 називається саме число
називається саме число  , якщо
, якщо 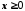 , число –
, число –  , якщо
, якщо 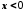 .
.1 2