
| МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ, МОЛОДЁЖИ И СПОРТА УКРАИНЫ МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ, МОЛОДЁЖИ И СПОРТА АВТОНОМНОЙ РЕСПУБЛИКИ КРЫМ РЕСПУБЛИКАНСКОЕ ВЫСШЕЕ УЧЕБНОЕ ЗАВЕДЕНИЕ “КРЫМСКИЙ ГУМАНИТАРНЫЙ УНИВЕРСИТЕТ” (Г. ЯЛТА) ИНСТИТУТ ЭКОНОМИКИ И УПРАВЛЕНИЯ КАФЕДРА МАТЕМАТИКИ, ТЕОРИИ И МЕТОДИКИ ОБУЧЕНИЯ МАТЕМАТИКЕ |
| ИГРОВЫЕ СИТУАЦИИ НА УРОКАХ МАТЕМАТИКИ 5-6 КЛАССА |
| Курсовая работа студентки 3 курса, направления подготовки“Математика” Вербовской А.В.(полное) Научный руководитель: ассистент кафедры к.пед.н. Зиненко И.Н. |
| Ялта, 2012 |
СОДЕРЖАНИЕ
ВВЕДЕНИЕ……………………………………………………………………….3
ГЛАВА 1. ПСИХОЛОГО-ДИДАКТИЧЕСКИЕ И МЕТОДИЧЕСКИЕ ОСНОВЫ ПРИМЕНЕНИЯ ИГР НА УРОКАХ МАТЕМАТИКИ
1.1. Методы активного обучения как средство активизации учебно-познавательной деятельности учеников………………………………………..6
1.2. Классификация игр на современном этапе развития системы образования……………………………………………………………………….9
1.3 Игровые ситуации на уроках математики 5-6 класса……………………..11
ВЫВОДЫ по I разделу………………………………………………………….13
ГЛАВА 2. ПРИМЕНЕНИЕ ИГРОВЫХ СИТУАЦИЙ НА УРОКАХ МАТЕМАТИКИ 5-6 КЛАССА
2.1. Игровые ситуации на уроке изложения нового материала………………14
2.2. Игровые ситуации на уроке закрепления изучаемого материала и выработки практических умений и навыков…………………………………..16
2.3. Игровые ситуации на уроке повторения, обобщения и систематизации изучаемого материала…………………………………………………………...20
ВЫВОДЫ по II разделу…………………………………………………………25
ОБЩИЕ ВЫВОДЫ………………………………………………………………26
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ……………………………..27
ПРИЛОЖЕНИЯ
ВВЕДЕНИЕ
Проблема качества школьного образования всегда была предметом обсуждения среди ученых, методистов и педагогов. Изменения общественных приоритетов последнего десятилетия прошлой эпохи определили новые аспекты в этом направлении. Интерес к указанной проблеме в основном проявлялся в контексте обоснования уровня учебных достижений учащихся путем анализа оценки результатов усвоенного ими учебного материала, умением оперировать знаниями, использовать их в конкретных ситуациях.
Современная школа призвана создать максимально благоприятные условия для формирования личности в целом, математического развития учащихся в частности. Одним из средств достижения и выполнения этих задач являются игровые ситуации. С середины 70-х гг. в отечественной школе обнаружилась опасная тенденция снижения интереса школьников к занятиям. На эту проблему педагогики отреагировали так называемыми нестандартными уроками, имеющими главной целью возбуждение и удержание интереса учащихся к учебному труду. Перечислю наиболее распространенные типы нестандартных уроков: уроки-соревнования, уроки типа КВН, театрализованные уроки, уроки с групповыми формами работы, уроки творчества, уроки-конкурсы, уроки-игры, уроки-ролевые игры. Основная роль в этих нестандартных уроках отводится игровым ситуациям.
Использование игры с целью воспитания можно найти в трудах классиков античной педагогики. Древнегреческие философы Платон, Аристотель, римский педагог Квинтилиан отдавали большую роль игре в воспитании и образовании. Их идеи рассмотрели и расширили в своих работах великие педагоги Я.А.Коменский, Д.Локк, Ж.Ж.Руссо, Ф.В.Фребель.
Игровые ситуации освещены в работах таких украинских ученых, как В.А.Сухомлинский, Н.П.Гузик, И.П.Подласый, А.С.Макаренко, Н.В.Слюсаренко.
Значительный вклад в решение этой проблемы внесли такие известные российские ученые и педагоги-новаторы, как Ш.А.Амонашвили, К.Д.Ушинский, С.А.Шмаков, В.Ф.Шаталов, П.П.Блонский, Г.В.Плеханов, С.Л.Рубинштейн, Л.С.Выготский и др.
Объект исследования – процесс изучения математики в 5-6 классах.
Предмет исследования – применение игровых ситуаций в процессе обучения учащихся на уроках математики 5-6 классов.
Цель: показать применение игровых ситуаций на уроках математики 5-6 класса как средство повышения уровня знаний учащихся.
Реализация поставленной цели требует решения следующих задач:
1. Проанализировать научно-методическую, психолого-педагогическую и учебную литературу по проблеме исследования.
2. Выявить значение и влияние игровых ситуаций на уроках математики 5-6 классов.
3. Показать применение игровых ситуаций на различных этапах урока математики с целью повышения уровня математических знаний учеников.
ГЛАВА 1. ПСИХОЛОГО-ДИДАКТИЧЕСКИЕ И МЕТОДИЧЕСКИЕ ОСНОВЫ ПРИМЕНЕНИЯ ИГР НА УРОКАХ МАТЕМАТИКИ
1.1. Методы активного обучения как средство активизации учебно-познавательной деятельности учеников
ВСТАВИТЬ ВВОДНЫЙ АБЗАЦ ПО ИСПОЛЬЗОВАНИЮ АКТИВНЫХ МЕТОДОВ + УЧЕНЫХ, КОТОРЫЕ ЗАНИМАЛИСЬ ИССЛЕДОВАНИЕМ ДАННОЙ ПРОБЛЕМЫ
Так, непосредственное вовлечение учащихся в активную учебно-познавательную деятельность в ходе учебного процесса связано с применением приемов и методов, получивших обобщенное название активные методы обучения. А.М.Смолкин дает следующее определение:
Методы активного обучения – способы активизации учебно-познавательной деятельности учащихся, которые побуждают их к активной умственной и практической деятельности в процессе овладения материалом, когда активный не только учитель, но и учащийся. [3]
Методы активного обучения предусматривают использование такой системы методов, которая направлена главным образом не на изложение готовых знаний и их воспроизведение, а на самостоятельное овладение учащимися знаний в процессе активной познавательной деятельности.
Важный вклад в классификацию методов активного обучения внесли такие ученые педагоги как М.М.Бирштейн, А.А.Вербицкий, В.И.Маршев и другие. [4, 5, 6] Поэтому существуют различные подходы, касающиеся классификации методов активного обучения.
Чаще всего используют классификацию А.М. Смолкина, а именно по характеру учебно-познавательной и игровой деятельности. Соответственно данной классификации, методы активного обучения подразделяют на:
Имитационные методы:
а) игровые методы:
- игровые процедуры и приёмы;
- игровые ситуации;
- дидактическая игра;
- деловые игры.
б) не игровые методы (анализ конфликтов, анализ проблемных ситуаций, диспуты, мозговой штурм, анализ конкретных ситуаций и др.).
Неимитационные методы (программное обучение, проблемная лекция и др.).
Игровые ситуации являются одним из методов активного обучения. Организовывая учебную деятельность на уроках математики, следует отдавать преимущество таким её формам, которые способствуют самовыражению и самоутверждению каждого ребенка. Такие возможности появляются в связи с использованием дидактических игр с предусмотренной личностно-деятельной направленностью учебно-воспитательного процесса. Заинтересовавшись игрой, ученики не замечают того, что обучаются, т.е. пополняют свои знания, умения и навыки, развивают внимание мышление, самостоятельность, адаптируются к условиям игры, развивают умение сотрудничества в коллективе. Незаурядного значения игре предоставил педагог С.А. Шмаков. Называя её „восьмым” чудом света, определял: „О знаменитой пирамиде Хеопса знают все.…А игра? Игра – самое интересное явление культуры…Игра, как тень, родилась вместе с человеком, стала его спутником, верным товарищем. Она заслуживает большого человеческого внимания, существенно большего, чем уделяют ей люди сегодня за те колоссальные учебные и воспитательные резервы, за великие педагогические возможности, которые в ней заложены” [].
Дидактическая игра – специально созданная игра, выполняющая определенную дидактическую задачу, скрытую от ребенка в игровой ситуации за игровыми действиями [2, c.]. В начале игра привлекает заданиями и трудностями, которые необходимо одолеть, а потом – радостью открытия, наслаждением от результатов.
Важную роль занимают дидактические математические игры, которые имеют общеобразовательные, развивающие и воспитательные функции, которые способствуют умственному развитию ребенка.
Итак, игровые ситуации являются одним из игровых методов, которые являются методами активного обучения.
1.2. Классификация игр на современном этапе развития системы образования
Игровая ситуация применяется с целью обеспечения интереса и продолжительности внимания, а также активности детей. Учебная игра способствуют достижению целей воспитания. Детская активность, желание действовать, творить, перестроить мир к лучшему выявляются в процессе игры.
Классификация ЧЬЯ педагогических игровых ситуаций:
Сюжетно-ролевые
Деловые
Организационно-деятельностные
Сюжетно-ролевые игровые ситуации характеризуются наличием задачи или проблемы, а также распределением ролей между участниками, реализация которых требует от них дополнительных знаний, относящихся к принятой роли. Участники такой игры имеют различные цели и исполняют разные роли, способствующие формированию умений и навыков. Также предполагается подражание участников в речевом и неречевом поведении и активное взаимодействие всех участников игры. Сюжетно-ролевые игры зачастую распределяются на ролевые, игры-драматизации и режиссерские.
В деловых игровых ситуация на основе игрового замысла моделируются жизненные ситуации. Суть деловой игры состоит в том, чтобы воссоздать некоторую профессиональную ситуацию в её стандартном виде, а также поиск оптимальных путей решения данной ситуации. А.Г. Хоменко делит учебные деловые игры профориентационного содержания в соответствии с основными дидактическими задачами на четыре типа:
1. Игры „Знатоки”. Основная дидактическая задача – усвоение базовых профессиональных знаний.
2. Игры „Умельцы”. Овладение профессиональными навыками и умениями действовать в стандартных ситуациях.
3. Игры „Искатели”. Осуществляется перенос знаний и умений в нестандартные ситуации, усвоение творческого опыта.
4. Игры „Профессионалы”. Комплексное применение профессиональных умений в ситуациях, максимально приближенных к производственным. [7, с.]
Организационно-деятельностные игровые ситуации предусматривают организацию коллективной мыслительной деятельности на основе развертывания содержания обучения в виде системы проблемных ситуаций и взаимодействия всех субъектов обучения в процессе анализа. Они могут быть связаны с формой построения учебного занятия (например, составление кроссворда или соревнование двух групп учащихся при взаимной постановке вопросов или выполнения практических заданий).
Все вышеперечисленные игры имеют широкий спектр целевых ориентаций, направленных на обучение, воспитание и развитие мотивации учащихся.
Если же игровая ситуация используется в качестве основы, но деятельность участников формализована, то есть имеются правила, жесткая система оценивания, предусмотрен порядок действий, регламент, то эти все компоненты можно считать компонентами дидактической игры.[8]
1.3. Игровые ситуации на уроках математики 5-6 классов
Возможность и целесообразность использования игровых ситуаций на уроках математики 5–6 классов в процессе изучения и закрепления нового материала различны в зависимости от дидактических целей урока.
В большинстве случаев игровые ситуации применяются в качестве вспомогательного средства для возбуждения познавательного интереса и создания проблемных ситуаций. Это настраивает учащихся на изучение определенного материала и, в отличие от дидактических игр, не требует дополнительного времени для разъяснения правил игры.
Игровые ситуации на уроках математики имеют большое значение, потому что у учеников 5-6 класса познавательный интерес неустойчив и напрямую зависит от узкоконкретного содержания их жизни. Поэтому можно превращать ситуацию урока в ситуацию нормальной детской жизни, где дети будут учиться в игре. И урок станет интереснее, дети будут меньше уставать, будет выполняться больший объем работы и при всем этом сохранится трудовая активность на протяжении всего урока. Игра для учащихся данного возраста класса – серьезное дело, потому что именно в ходе игры у них формируется настойчивость, организованность, позитивное отношение к обучению, ведь в игру включаются и дети, которые на обычном уроке работают не активно, или не работают вовсе.
На уроках математики, как и на уроках других дисциплин, очень выгодно использовать игровой материал. Это даст возможность углубить знания, заинтересует предметом, каждый ученик сделает для себя маленькое открытие и будет радоваться ему. А главное – будет ждать, когда же наступит время следующего занятия.
Активизировать деятельность учащихся в процессе овладения математическими знаниями можно путем нестандартной формы представления игры. У детей вызовет внутренний позитивный отклик игра тогда, когда она будет характеризоваться новизной, неожиданностью, необычностью, несоответствием привычным представлениям.
На уроках математики для учащихся 5-6 класса можно применять игровые ситуации такого типа:
учебные, где игровой процесс сопровождается освоением содержания обучения;
ролевые, где ученики берут на себя выполнение определенных ролей.
Каждая игра приносит ученикам моральное и умственное удовольствие, поднимает их настроение. Для учителя результат игры является показателем уровня достижения учащихся в усвоении тех или иных знаний или в их применении.
Для создания игровых ситуаций на уроках математики используются:
- исторические экскурсы,
- жизненные факты,
- научно-популярные рассказы,
- отрывки из литературных произведений.
Значение игровой ситуации велико. Являясь развлечением, отдыхом, она способна перерасти в обучение.
На уроках математики можно использовать широкий спектр игровых ситуаций, направленных на обучение и повышение мотивации учащихся: задачи в стихах; задачи – рисунки, занимательный квадрат; задачи – шутки; математический фокус; математическая эстафета; головоломки; ребусы; задачи на смекалку и многое др.
Игровая ситуация является перспективной формой обучения, так как она способствует созданию благоприятного психологического климата на уроке, усиливает мотивацию и активную деятельность учащихся, повышает эффективность учебного процесса, помогает сохранить интерес учащихся к изучаемому предмету.
Когда игровая ситуация используется как дидактический метод, она всегда приводит к запланированному результату. [9]
ВЫВОДЫ по I разделу
Национальная доктрина развития образования ставит перед учителем задачу создать ребенку условия для его максимального самоопределения и саморазвития. Для этого процесс обучения должен быть сконструирован с максимальным приближением к запросам и возможностям ребёнка.
Действенным способом привлечения учащихся к процессу обучения и к получению радости от познания является учебная игра. Именно игра имеет большое значение в удовлетворение человеческой потребности познания мира, входя в психический и физический мир ребенка с первых дней его существования.
Особенность игровой деятельность состоит в том, что в ней успешно усваивается содержание учебной деятельности. Использование игры способствует смене мотивов поведения, раскрытию новых источников развития познавательных сил, повышению самооценки учащихся, установлению дружеских отношений в группе и коллективе, развитию воображения и т.д.
ГЛАВА 2. ПРИМЕНЕНИЕ ИГРОВЫХ СИТУАЦИЙ НА УРОКАХ МАТЕМАТИКИ 5-6 КЛАССА
2.1. Игровые ситуации на уроке изложения нового материала.
Урок изложения нового материала – это такой тип урока, основная часть которого посвящена подаче новых знаний и первоначальному их закреплению []. Можно использовать различные способы подачи новых знаний – наблюдение за явлениями природы, проведение представленного или демонстративного эксперимента – которые должны поставить вопросы таким образом, чтобы ученики, отвечая на них, самостоятельно делали выводы. Игровые ситуации во время такого урока помогают сформировать знания у учащихся, а это основная цель урока.
Урок изучения нового материала “Доли и обыкновенные дроби” в 5 классе.
Цели урока: научить понимать, что такое доля, половина, треть и четверть, уметь записывать дроби, изображать дроби на координатном луче.
Оборудование: проектор, мандарин, кроссворд.
Ход урока
1. Организационный момент.
Сообщение темы и цели урока.
2. Устные упражнения.
Учитель: Кто будет внимателен и активен на уроке, тот узнает о новом математическом термине (на доске выполнен черным маркером кроссворд с заданиями, дети записывают красным маркером, а слово по вертикали синим маркером).
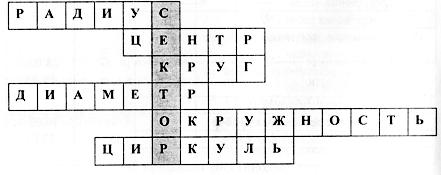
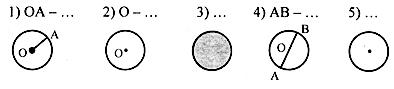
6) название инструмента для вычерчивания окружностей.
Учитель: Прочитайте слово, получившееся в выделенном столбце кроссворда.
Ответ: сектор – часть круга, ограниченная двумя радиусами (демонстрация секторов, вырезанных из цветного картона).
3. Изучение нового материала.
Материал сопровождается презентацией.
План изложения:
1. Понятие и определение доли (продемонстрировать на мандарине).
2. Название долей
3. Запись обыкновенной дроби, определение числителя, знаменателя.
4. Что показывает числитель? Что показывает знаменатель?
4. Закрепление.
1. Устные упражнения по учебнику.
2. Задачи, выполняемые в тетрадях письменно.
5. Итог урока.
6. Домашнее задание.
НЕОБХОДИМО СДЕЛАТЬ АБЗАЦ ВЫВОДА ПО ЭТОМУ ПУНКТУ ДОБАВИТЬ ЕЩЕ КАКОЙ-ЛИБО ПРИМЕР
2.2. Игровые ситуации на уроке закрепления изучаемого материала и выработки практических умений и навыков.
Урок закрепления изучаемого материала и выработки практических умений и навыков проводится после изучения отдельной темы или раздела учебной программы и направлен на организацию рассредоточенного повторения пройденного материала учащимися с целью его более глубокого осмысления и усвоения.
Урок закрепления изучаемого материала “Умножение рациональных чисел” в 6 классе.
Цели урока: закрепить умения и навыки решать упражнения на умножение рациональных чисел; способствовать формированию и развитию у учащихся интеллектуальных и творческих способностей в процессе обобщения и систематизации материала; воспитать любовь к природе.
Ход урока
1. Организационный момент.
Сообщение темы и цели урока.
2. Мотивация обучения.
Учитель. Сегодня мы будем путешествовать по страницам Красной книги. Охрана окружающей среды – это защита нашего мира и его дикой природы. Самые обаятельные и красивые создания природы оказываются самыми хрупкими звеньями живого мира. За последние годы больше двадцати видов растений перешли в разряд редких и исчезающих. Такие виды растений заносят в Красную книгу, которая была создана по идеи известного английского зоолога, профессора Питера Скотта в 1963г.
Международная Красная книга состоит из нескольких больших томов, в которые включено более 320 видов и подвидов млекопитающих, 485 видов птиц, более 140 видов пресмыкающихся, приблизительно 200 видов рыб.
Каллиграфическая минутка. Запишите дробь, числитель которой равен количеству букв в слове “красная”, а знаменатель дроби – количество звуков в слове «книга».
Ответ.
Вопросы:
Какова есть дробь
Как выделить целую часть из неправильной дроби?
Выделите целую часть из дроби
3. Решение упражнений и задач.
3.1. Устный счет с записью ответов.
Учитель. „Стой, будь осторожен!” – предупреждает красный свет светофора. И все это понимают. “Остановитесь, перестаньте уничтожать природу, потому что будет беда!” – предостерегает Красная книга. Но понимают это, к сожалению, не все. В Украине тоже есть Красная книга, которая состоит из двух томов. В первый том внесено 544 растений, а во второй – 382 вида животных, которым грозит опасность. Год её утверждения мы узнаем, выполнив все задания устного счета с записью ответов. Учитель читает задания каждого из двух вариантов, а ученики записывают на заранее подготовленном листе бумаги только ответы. После окончания учащиеся вместе с учителем проверяют правильность выполнения заданий.
Вариант 1
1. Выполнить действия:
2. Решить уравнение 5,4 – x = -3,6;
3. Вычислить:
4. Вычислить:
Вариант 2
1. Выполнить действия:
2. Решить уравнение 1,2 – x = -7,8;
3. Вычислить:
4. Вычислить:
Итак, в Украине 29 октября 1992 года Постановлением Верховной Рады Украины утверждена Красная книга, а 7 февраля 2002 года был принят Закон Украины “О Красной книге Украины”.
3.2. Решение уравнений.
Учитель. Природа требует нашей помощи. Сегодня вы узнаете больше о растениях, которые нуждаются в вашей защите и спасении.
За окном ещё белеет снег, а под снеговым одеялом уже пробуждается новая жизнь. И вот появляются первые посланцы зеленоглазой Весны. Кто они? Чтобы узнать это, необходимо решить уравнения.
1. (x - 3) : (-2,5) = 7; x = -14,5.
2. -6,8 (x - 4) = 0; x = 4.
3. (x + 7,2) (x – 8,1) = 0; x = -7,2 или x = 8,1
Учитель. Расставьте корни данных уравнений в порядке возрастания и каждое число замените составляющим.
Ответ. - 14,5 ___под; - 7,2___снеж; 4___ни; 8,1___ки.
Ученики составляют слово “подснежники”.
Далее задание составить слово и угадать (выполнение соответствующих упражнений). Ключевое слово – пролески.
Благодаря своей красоте и тому, что они одни из первых открывают весенний карнавал цветения, пролески почти полностью истреблены. Они занесены в Красную книгу и требуют охраны.
4. Домашнее задание.
5. Подведение итогов урока.
Знакомство со страницами Красной книги вы продолжите на уроках биологии и географии. Охраняйте природу, потому что все виды животных и растений необходимы. Пусть природа радует человеческий глаз своей красотой.
Игровую ситуацию “Угадай слово” можно использовать при закреплении материала по любой теме курса математики 5-6 классов. Например, тема „Сложение и вычитание смешанных чисел”.
Даётся задание: Расшифруйте название дерева, похожего на ёлку, у которого шишки растут вверх, а не вниз. Для этого решите примеры:

-
Т
А
П
Х
И




Такое задание очень нравиться учащимся, они быстро включаются в деятельность, стараются не ошибиться при вычислениях, чтобы первыми прийти к ответу на поставленный вопрос.
АБЗАЦ ВЫВОДА ПО ЭФФЕКТИВНОСТИ ИСПОРЛЬЗОВАНИЯ ИГОР НА УРОКАХ ТАКОГО ТИПА
2.3. Игровые ситуации на уроке повторения, обобщения и систематизации изучаемого материала.
ВВОДНЫЙ АБЗАЦ
Урок повторения, обобщения и систематизации изучаемого материала „Умножение десятичных дробей” в 5 классе.
Цели урока: обобщить и систематизировать знания, умения, навыки учащихся по изученной теме; развивать логическое мышление, познавательную активность учащихся, творческие способности и вычислительные навыки; воспитывать интерес к обучению.
Оборудование: карточки, схемы, модель прямоугольного параллелепипеда.
Ход урока
1. Организационный момент.
Сообщение темы и цели урока.
Учитель. За окном – пасмурный зимний день. А я так хочу, чтобы в ваших душах было солнечно. Надеюсь, что из ваших сердец излучается тепло, ласка, доброта, нежность и желание помочь друг другу. Сегодня ми проведем необычный урок. Я жду от вас активности, внимательности, четких ответов и смелых идей. Итак, окунемся в сказочный мир.
2. Актуализация опорных знаний.
Учитель. Жила добрая женщина, но не было у неё детей. Фея подарила ей зернышко, с которого появилась на свет маленькая девочка – Дюймовочка. Хорошо жилось девочке у женщины, пока старая жаба не похитила её, чтобы поженить на своем ужасном сыне. Чтобы помочь девочке убежать от жабы, нам нужно проверить домашнее задание и правильно ответить на вопросы.
(Два учащихся выполняют у доски упражнения с домашней работой, другие – задание учителя.)
Выполнение заданий:
1. Какие действия с десятичными дробями вы умеет выполнять?
2. Как прибавить и отнять десятичную дробь?
3. Назовите компоненты действия умножения.
4. Как умножить десятичные дроби?
5. Сколько знаков после запятой нужно отделить запятой в произведении чисел:
17,75 ∙ 1,534;
0,0375 ∙ 9,52;
3,5 ∙ 12,479;
1, 02349 ∙ 0, 12?
6. Сформулируйте правила умножения десятичных дробей на разрядные единицы.
7. Какие законы умножения помогают быстро выполнять вычисления? Найдите их в учебнике и запишите в тетради.
8. Вычислите устно:
0,2 ∙ 0,3; 25,8 ∙ 10; 123,5 ∙ 0,01; 3,23 ∙ 2; 6,2 ∙ 4; 5,1 ∙ 3; 1,11 ∙ 0,4; 2 ∙ 0,5.
Исправьте в записях ошибки:
1,7 ∙ 0,1=17; 3,9 ∙ 0=3,9; 10,1 ∙ 100=10,10
(На доске заранее прикреплены листы бумаги, на каждом из них напечатаны примеры.)
Учитель. Учение о десятичных дробях впервые преподал в XVвеке самаркандский математик и астроном Джемшид ибн Масуд аль-Каши. Целую и дробную часть он отделял вертикальной черточкой или записывал их чернилами разного цвета.
В 1585 году фламандский ученый Симон Стевин в своей книге «Десятая» изложил правила действий с десятичными дробями.
Запятую, как знак, который разделяет целую и дробную часть числа предложил шотландский математик Джон Непер в XVI веке, но еще ранее запятую применил немецкий ученый Иоганн Кеплер (1571-1603 гг.). А в России учение о десятичных дробях впервые изложил Л.П.Магницкий в 1703 году в своем учебнике „Арифметика”.
3. Решение упражнений.
Учитель. Молодцы! Вы помогли Дюймовочке убежать от жаб на листочке лилий. И чтобы жабы не поймали девочку, составим и решим задачу по условию. Помним, что Дюймовочка плывет на листочке по течению реки.
(На доске заранее прикреплен лист бумаги, на котором напечатаны условия задачи.)
Учитель назначает ученика, который комментирует ход решения задачи.
Дано:
v=1,2 км/ч;
t=8 ч;
s=? км.
Учитель. – Что известно по условию задачи?
– Сформулируйте вопрос задачи.
–По какой формуле вычисляется расстояние, преодоленное Дюймовочкой?
Ответ. 1,2 ∙ 8 = 9,6 (км).
Учитель. Листочек принес Дюймовочку в далекий край. Давайте построим мостик, чтобы девочка смогла сойти на берег. Для этого найдем числа a, b, c, которых не хватает в цепочке вычислений.
(На доске заранее прикреплен лист бумаги, на котором изображена схема.)
-4,54 ∙2,6 ∙10
29,04 → a → b → c
Ответ. а = 24,5; b = 63,7; c = 637.
Учитель. Дюймовочка перешла через мостик. Устала, проголодалась, замерзла и плачет. Услышала это тётя Мышка и предложила ей перезимовать в её норке, но с одним условием – если девочка вычислит объем корзинки, в которой будут беречься припасы на зиму. А вот и сама корзинка (модель прямоугольного параллелепипеда). Поможем Дюймовочке? (Ученики соглашаются.)
– Какая геометрическая фигура перед вами?
– Сколько величин имеет прямоугольный параллелепипед?
– По какой формуле вычисляется объем параллелепипеда?
Работаем в группах (назначаются консультанты в каждой группе).
А размеры этой корзинки такие (учитель раздает группам карточки).
Задание для 1-ой группы
Округлите числа до единиц и найдите объем параллелепипеда:
a=30,15 см;
b=10,2 см;
c=5,62 см.
Ответ. a=30 см, b=10 см, c=6 см, V=1800 см3.
Задание для 2-ой группы
Вычислите объем параллелепипеда и округлите результат до единицы:
a=21,7 см;
b=?, на 10,6 см меньше, чем a;
c=10 см.
Ответ. b=11,1 см, V=21,7 ∙ 11,1 ∙ 10=2408,7 ≈ 2409 см3.
Один учащийся работает у доски. Измеряет длину, ширину, высоту модели и вычисляет объем параллелепипеда.
Ответ. a =_____, b =_____, c =_____, V =______ .
Учитель. Осталась Дюймовочка зимовать у тёти Мышки, и сосед Крот задумал пожениться на ней. Снова девочка нуждается в помощи. Нужно согреть Ласточку, которая поможет Дюймовочке убежать. Группы будут отвлекать внимание Крота, решая упражнения, а один из учеников отогреет Ласточку, поставив вместо звездочек пропущенные цифры.
Задание для 1-ой группы
Решите уравнение (х + 1,7) : 2,3 = 1,84
Ответ. 2,532.
Задание для 2-ой группы
Решите уравнение (х + 3,5) : 10 = 2,24
Ответ. 18,9.
Учитель. Дети, вы отогрели Ласточку, этим помогли Дюймовочке улететь от Крота в теплые страны. Чтобы этот перелет был для них легким, вычислим удобным способом такие задания.
(Ученики работают в парах, каждая из которых получает карточку с дифференцированными заданиями, один ученик работает у доски, выполняя индивидуальные задания.)
Учитель. Молодцы! Благодаря вам Дюймовочка оказалась в чудесной Стране цветов. Вы помогли Дюймовочке преодолеть все препятствия. В Стране цветов она встретила принца эльфов. Решив задачу, мы узнаем сколько же подарков получили они на свою свадьбу.
Задача. Пчелки подарили 1,6 кг меда, это в три раза меньше, чем сладкой пыльцы, которую принесли бабочки. А Ласточка подарила корзинку с клубникой, которая весила в 0,1 раз больше, чем мед с пыльцой вместе. Сколько всего сладостей получили супруги?
Решение.
1) 1,6 ∙ 3 = 4,8 (кг);
2) 1,6 + 4,8 = 6,4 (кг);
3) 6,4 ∙ 0,1 = 0,64 (кг);
4) 6,4 + 0,64 = 7,04 (кг).
Ответ. 7,04 кг.
4. Подведение итогов урока.
Учитель. Дети, вы хорошо поработали и помогли Дюймовочке найти своё счастье. От нее привет – хорошие оценки и пожелание успехов в учебе. (Учитель комментирует оценки.)
5. Домашнее задание.
АБЗАЦ ВЫВОДА ПО ЭФФЕКТИВНОСТИ ИСПОРЛЬЗОВАНИЯ ИГОР НА УРОКАХ ТАКОГО ТИПА
ВЫВОДЫ по II разделу
Особенностью учебной игры как формы обучения состоит в том, что она достигает своей цели незаметно для учащегося, не требует никаких способов насильства над личностью. Поэтому для успешного руководства играми важно уметь приобрести доверие учеников. Это возможно, когда педагог относиться к игре серьёзно, с интересом, понимает детей, их переживания, дает простор детской инициативе и творчеству.
Игровые ситуации могут использоваться на различных видах урока и на разных его этапах. Игровые ситуации помогают с легкостью и доступностью понять учащимися новый материал, а также сделать обычный урок повторения и закрепления материала ярким и незабываемым.
Игры дополняют традиционные формы обучения, способствуют активизации процесса обучения, делая его более увлекательным.
ОБЩИЕ ВЫВОДЫ
В процессе работы над темой, на основе рассмотренной психолого-педагогической и методической литературы по данному вопросу, а также в результате исследования, выяснено, что в педагогической работе большое внимание уделяется дидактической игре и игровым ситуациям на уроке. Выявлено их существенное значение для получения, усвоения и закрепления новых знаний у учащихся.
Дидактическая игра и игровые ситуации позволяют не только активно включить учащихся в учебную деятельность, но и активизировать их познавательную деятельность. Игра помогает учителю донести до учащихся трудный материал в доступной форме. Игровые ситуации могут быть использованы, как и на этапах повторения и закрепления, так и на этапах изучения нового материала. Они должны в полной мере решать как образовательные задачи урока, так и задачи активизации познавательной деятельности, и быть основной ступенью в развитии познавательных интересов учащихся.
Благодаря играм удаётся сконцентрировать внимание и привлечь интерес даже у самых несобранных учеников. Вначале их увлекают только игровые действия, а затем и то, чему учит та или иная игра. Постепенно у учащихся пробуждается интерес и к самому предмету обучения. Игры на уроках – это целенаправленная творческая деятельность, в процессе которой обучаемые глубже и ярче постигают явления окружающей действительности и познают мир.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Подласый И.П. Педагогика. Новый курс: учебник для студентов пед. вузов. Кн.1: Общие основы. Процесс обучения. – М.: Гуманит. изд. центр Владос. 1991 – 576 с.
2. Карпенко Л.А. Психология развития: словарь. – М.: Пер сэ. 2006. – 176 с.
3. Смолкин А.М. Методы активного обучения. – М.: Высшая школа. 1991. – 30 с.
4. Бирштейн М.М. Деловые игры. – Рига: Авотс. 1989. – 304 с.
5. Вербицкий А.А. Активное обучение в высшей школе: Контекстный анализ. – М.: Высшая школа. 1993. – 207 с.
6. Маршев В.И., Лукаш Е.Н. Методы активного обучения управлению. – Изд.: МГУ. 1991. – 349 с.
7. Хоменко А.Г. Учебные деловые игры как средство формирования профессиональных умений студентов техникумов и колледжей. – К. 1994. – 148 с.
8. Слюсаренко Н.В. Розвиток творчих здібностей учнів 5-9 класів на уроках обслуговуючої праці засобами ігрової діяльності: навч.-метод. посіб. – Херсон. 2002. – 148 с.
9. Коваленко В.Г. Дидактические игры на уроках математики: кн. для учителя. – М.: Просвещение. 1990. – 97 с.
10. Кучерова Г.М. Методика проведення гри як засобу активізації пізнавальної діяльності учнів на уроці. – Харкiв: Вид. Группа «Основа». 2011. – 144 с. – (Серiя «Адмiнiстратору школи»).
11. Соловей О.М. Дидактические игры на уроках математики. 2010.