1   2   3
Ім'я файлу: курсова 3 курс 1 семестр.docx
Розширення: docx
Розмір: 218кб.
Дата: 06.05.2021
скачати
Пов'язані файли:
ср3.doc
17план конспект уроку Покупки у Лондоні.docx


Національний університет «Чернігівський колегіум» імені Т.Г.Шевченка
Кафедра математики та економіки

КУРСОВА РОБОТА
з дисципліни Аналітична геометрія
на тему:
«Конструктивні геометричні задачі та методи їх розв’язування»

студентки 3 курсу 31 групи
Галузі знань 0402
Фізико-математичні науки
напряму підготовки 6.040302

Асатурян Марії Павлівни
Керівник — Музиченко С.В.

Національна шкала ____________

Кількість балів _______

Оцінка ECTS____


Члени комісії: ____________________________________
(підпис) (прізвище та ініціали)

___________________________________
(підпис) (прізвище та ініціали)

________________________________
(підпис) (прізвище та ініціали)

Чернігів 2018 р.

«Конструктивні геометричні задачі та методи їх розв’язування»

План:

Вступ

Розділ 1. Загальні відомості про конструктивні геометричні задачі

    1. Поняття конструктивної геометричної задачі

    2. Аксіоми циркуля та лінійки

    3. Основні задачі на побудову

    4. Схема розв’язування задач на побудову

Розділ 2. Методи розв’язування конструктивних геометричних задач

2.1 Метод зведення задачі на побудову до найпростіших

2.2 Метод перетину множин (ГМТ)

2.3 Методи перетворень

2.3.1 Паралельне перенесення

2.3.2 Симетрія

2.3.3 Поворот

2.3.4 Інверсія

2.3.5 Гомотетія

2.4 Алгебраїчний метод

Висновки

Список використаної літератури

Вступ

Вся історія геометрії й деяких інших розділів математики тісно пов'язана з розвитком теорії геометричних побудов. Найважливіші аксіоми геометрії, сформульовані основоположником наукової геометричної системи Евклідом близько 300 р. до н.е., ясно показують яку роль зіграли геометричні побудови у формуванні геометрії. «Від усякої точки до всякої точки можна провести пряму лінію», «Обмежену пряму можна безупинно продовжувати», «Із усякого центра й усяким розчином циркуля може бути описане коло» – ці постулати Евкліда явно вказують на основні положення конструктивних методів у геометрії древніх.

Давньогрецькі математики вважали «істинно геометричними» лише побудови, здійснені лише циркулем і лінійкою, не визнаючи «законним» використання інших засобів для розв’язання конструктивних задач. При цьому, відповідно до постулатів Евкліда, вони розглядали лінійку як необмежену й однобічну, а циркулю приписувалася властивість креслити кола будь-яких розмірів. Задачі на побудову циркулем і лінійкою вже більше ста років є традиційним матеріалом шкільного курсу геометрії.

Об'єктом дослідження роботи є геометричні задачі на побудову.

Предмет дослідження – різні методи розв’язування задач на побудову.

Ціль даної роботи – виклад розв’язування геометричних задач на побудову (конструктивних задач) за допомогою різних методів.

Розділ 1. Загальні відомості про конструктивні геометричні задачі

1.1 Поняття конструктивної геометричної задачі

Розділ геометрії, в якому вивчаються геометричні побудови, називають конструктивною геометрією. Основним поняттям конструктивної геометрії є поняття побудувати геометричну фігуру, розглядаються конструктивні задачі.

В конструктивних задачах йдеться про побудову геометричних фігур заданими засобами. Зазвичай за допомогою використання циркуля та лінійки. При цьому маємо на увазі ідеальні побудови. Окрім побудов циркулем і лінійкою, розглядаються побудови за допомогою інших засобів (наприклад за допомогою однієї лінійки).

У кожній задачі на побудову потрібно за деякими заданими фігурами побудувати шукану фігуру, яка задовольняє ті чи інші умови. До цього ж вказується за допомогою яких креслярських інструментів треба виконувати побудови.

Основні задачі на побудову розглядаються в кожному курсі елементарної геометрії. Існує п’ять основних задач на побудову:

  1. Побудувати трикутник з даними сторонами a, b, c.

  2. Відкласти від даної пів прямої в даній півлощині кут, що дорівнює даному куту.

  3. Побудувати бісектрису даного кута.

  4. Поділити даний відрізок пополам.

  5. Через дану точку провести пряму, перпендикулярну до даної прямої.



    1. Аксіоми циркуля та лінійки

Для конструктивної геометрії необхідно мати точний і для математичних цілей повний опис того чи іншого інструмента. Такий опис дається у вигляді аксіом. Ці аксіоми в абстрактній математичній формі виражають ті властивості реальних креслярських інструментів, які використовуються для геометричних побудов. Найбільш уживаними інструментами геометричних побудов є: лінійка (однобічна), циркуль, двостороння лінійка (з паралельними краями) і деякі інші.

Сформулюємо відповідні аксіоми.

1. Аксіома лінійки. Лінійка дозволяє виконати наступні геометричні побудови:

а) побудувати відрізок, що з'єднує дві побудовані точки;

б) побудувати пряму, яка проходить через дві побудовані точки;

в) побудувати промінь, що виходить із побудованої точки й проходить через іншу побудовану точку.

2. Аксіома циркуля. Циркуль дозволяє виконати наступні геометричні побудови:

а) побудувати коло, якщо побудовані його центр та відрізок, що дорівнює радіусу кола (або його кінці);

б) побудувати кожну із двох додаткових дуг кола, якщо побудовані його центр й кінці цих дуг.

3. Аксіома двосторонньої лінійки. Двостороння лінійка дозволяє:

а) виконати кожну з побудов, перерахованих в аксіомі 1;

б) у кожній з напівплощин, утворених побудованою прямою, побудувати пряму, паралельну даній прямій і розташовану від неї на відстані a, де a – фіксований для даної лінійки відрізок (ширина лінійки);

в) якщо побудовані дві точки А й В, то встановити чи буде АВ більше деякого фіксованого відрізка h(ширина лінійки), і якщо 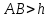, то побудувати дві пари паралельних прямих, що проходять відповідно через точки A й B і віддалених одна від іншої на відстані h.

4. Аксіома прямого кута. Прямий кут дозволяє:

а) виконати побудови, перераховані в аксіомі лінійки;

б) через дану точку площини провести пряму, перпендикулярну деякій побудованій прямій;

в) якщо побудований відрізок і деяка фігура Ф, то встановити, чи містить фігура Ф точку, з якої цей відрізок видний під прямим кутом, і якщо така точка існує, то побудувати таку точку.

Крім перерахованих інструментів, для геометричних побудов можна користуватися й іншими інструментами: довільним кутом, косинцем, лінійкою з оцінками, парою прямих кутів, різними пристосуваннями для креслення спеціальних кривих та ін. Геометричні побудови виконуються щоразу із певними, наперед зазначеними інструментами, причому набір інструментів характеризується певною системою аксіом.

Розв’язати задачу на побудову за допомогою циркуля й лінійки – значить звести її до сукупності п'яти елементарних побудов, які заздалегідь вважаються здійсненними. Перелічимо їх.

1. Якщо побудовані дві точки А та В, то побудовано пряму АВ, яка їх з'єднує, а також відрізок АВ і кожний із променів АВ і ВА (аксіома лінійки).

2. Якщо побудовано точку О и відрізок АВ, то побудовано коло із центром у точці О і радіусом АВ, а також кожна з дуг цього кола.

3. Якщо побудовані дві прямі, то побудовано точку їхнього перетину (якщо вона існує).

4. Якщо побудовано пряму й коло, то побудовано кожну із точок їхнього перетину (якщо вона існує).

5. Якщо побудовано два кола, то побудовано кожну із точок їхнього перетину (якщо вона існує).


    1. Основні задачі на побудову

Приведення розв’язання кожної задачі до елементарних побудов робить розв’язання досить громіздким, тому часто розв’язання задачі зводять до так званих основних побудов. Вибір деяких побудов у якості основних певною мірою довільний.

Під значенням «основні побудови» маємо на увазі опорні задачі, сформулюємо їх(основні побудови):

Позиційні:

  1. Відкласти на даному промені від його початку відрізок, який рівний даному.

  2. Відкласти від даного променя в дану півплощину кут, рівний даному.

  3. Побудувати трикутник за трьома сторонами.

  4. Побудувати трикутник за двома сторонами та кутом між ними.

  5. Побудувати трикутник за стороною і двома прилеглими кутами.

  6. Побудувати бісектрису даного нерозгорнутого кута.

  7. Побудувати серединний перпендикуляр даного відрізка.

  8. Побудувати середину даного відрізка.

  9. Побудувати пряму, яка проходить через дану точку перпендикулярно до даної прямої. (Випадки: а) точка лежить на прямій; б) точка не лежить на прямій).

  10. Побудувати пряму, яка проходить через дану точку паралельно даній прямій.

  11. Побудувати прямокутний трикутник за гіпотенузою і гострим кутом.

  12. Побудувати прямокутний трикутник за гіпотенузою і катетом.

  13. Побудувати дотичну до кола, яка проходить через дану точку на цьому колі.

  14. Дано коло (О;r) і точка А, що не лежить на ньому. Побудувати дотичну до кола, яка проходить через точку А.

  • Фігури, що задовольняють умові задачі, можуть розрізнятися як формою та розмірами, так і положенням на площині. Розходження в положенні на площині приймаються або не приймаються в розрахунок залежно від формулювання самої задачі на побудову, а саме залежно від того, передбачає або не передбачає умова задачі певне положення шуканої фігури щодо яких-небудь даних фігур. Пояснимо це прикладах.

Задача 1. Розглянемо наступну найпростішу задачу: побудувати трикутник за трьома сторонами і кутом між ними.

Точний зміст цієї задачі полягає в наступному: побудувати трикутник так, щоб дві сторони його були відповідно рівні двом даним відрізкам, а кут між ними був рівним даному куту. Тут шукана фігура (трикутник) пов'язана з даними фігурами (два відрізки й кут) тільки співвідношеннями рівності, розташування ж шуканого трикутника відносно даних фігур байдуже. У цьому випадку легко побудувати трикутник АВС, що задовольняє умові задачі. Всі трикутники, рівні трикутнику АВС, також задовольняють умові поставленої задачі. Однак немає ніякого сенсу розглядати ці трикутники як різні розв’язки даної задачі, тому що вони відрізняються один від одного тільки положенням на площині, про що в умові задачі нічого не сказано. Тому будемо вважати, що задача має єдиний розв’язок.

Отже, якщо умова задачі не передбачає певного розташування шуканої фігури відносно даних фігур, то шукатимемо тільки всі нерівні між собою фігури, що задовольняють умові задачі. Можна сказати, що задачі цього роду розв’язуються «з точністю до рівності».

Це означає, що задача вважається розв’язаною, якщо: 1) Побудоване деяке число нерівних між собою фігур Ф1, Ф2, … Фn, що задовольняють умовам задачі. 2) доведено, що будь-яка фігура, що задовольняє умовам задачі, дорівнює одній із цих фігур.

При цьому вважається, що задача має n різних рішень.

Задача 2. Розглянемо тепер задачу трохи іншого змісту: побудувати трикутник так, щоб однією його стороною служив даний відрізок ВС, інша сторона дорівнювала іншому даному відрізку l, а кут між ними дорівнював даному куту α. У цьому випадку умова задачі передбачає певне розташування шуканого трикутника щодо однієї з даних фігур (саме щодо відрізка ВС). Як видно на рис. 2.1, може існувати до чотирьох трикутників, що задовольняють умові цієї задачі.



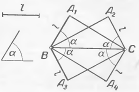Рис. 2.1
Вони рівні між собою, але по різному розташовані щодо даної фігури ВС. У цьому випадку повне розв’язки задачі передбачає побудову всіх цих трикутників. Вважається, що дана задача має до чотирьох різних розв’язків, що розрізняються своїм розташуванням щодо даної фігури.



1.4 Схема розв’язування задач на побудову

Питання про вибір тієї або іншої схеми рішення конструктивної задачі є чисто методичним питанням. Розв’язання конструктивної геометричної задачі є цілком правильним, якщо воно проведено за наступною схемою:

  1. Встановлюється остаточне число випадків, що вичерпують всі можливості у виборі даних.

  2. Для кожного випадку дається відповідь на питання, чи має задача розв’язки та скільки.

  3. Для кожного випадку, коли задача має розв’язання, дається спосіб знаходження (за допомогою даних геометричних інструментів) кожного з можливих розв’язків або встановлюється, що воно не може бути отримано даними засобами.

При розв’язуванні конструктивних задач користуються відомою схемою розв’язання, що складається з наступних чотирьох етапів:

1) аналіз;

2) побудова;

3) Доведення;

4) дослідження.

Аналіз. Це підготовчий і в той же час найбільш важливий етап розв’язання задачі на побудову, тому що саме він дає ключ до розв’язання задачі. Мета аналізу складається з встановлення таких залежностей між елементами шуканої фігури й елементами даних фігур, які дозволили б побудувати шукану фігуру. Це досягається за допомогою побудови креслення, що зображує дані й шукані фігури приблизно в тому розташуванні, як це задано умовою задачі. Іноді побудову креслення супроводжують словами: «припустимо, що задача вже розв’язана».

На допоміжному кресленні варто виділити дані елементи й найважливіші шукані елементи. Якщо допоміжне креслення не підказує безпосереднього способу побудови шуканої фігури, то намагаються виявити яку-небудь частину шуканої фігури або взагалі деяку фігуру, що може бути побудована, і якою потім можна скористатися для побудови шуканої фігури. Далі вивчають залежності між ними, поки не стане зрозумілим у якій послідовності слід виконувати побудови.

Побудова. Даний етап розв’язування полягає в тому, щоб указати послідовність основних побудов (або раніше розв’язаних задач), які досить зробити, щоб шукана фігура була побудована.

Побудова звичайно супроводжується графічним оформленням кожного його кроку за допомогою інструментів, прийнятих для побудови.

Задача 3. Побудувати коло, вписане в даний трикутник АВС. Для побудови шуканої окружності потрібно послідовно побудувати:

а) бісектриси яких-небудь двох внутрішніх кутів даного трикутника;

б) точку їхнього перетинання О;

в) пряму, що проходить через точку О, перпендикулярно прямій АВ;

г) відрізок ОМ проведеного перпендикуляра;

д) окружність (О, ОМ).
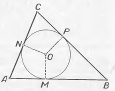Таким чином, кожна із прямих АС і ВС перпендикулярна до відповідного радіуса, що лежить на колі, тому кожна із цих прямих дотикається до побудованого кола.

Дослідження. При побудові звичайно обмежуються відшуканням одного якого-небудь розв’язку, причому передбачається, що всі кроки побудови дійсно здійсненні. Для повного розв’язку задачі потрібно ще з'ясувати наступні питання:

а) чи завжди (тобто при чи будь-якому виборі даних) можна виконати побудову вибраним способом;

б) чи можна і як побудувати шукану фігуру, якщо вибраний спосіб не можна застосувати;

в) скільки розв’язків має задача при кожному можливому виборі даних.

Розгляд всіх цих питань і становить дослідження. Таким чином, дослідження має на меті встановити умови можливості розв'язання й визначити число розв’язків.

Задача 4. Дано коло (О;r)і точка А, що не лежить на цьому колі. Побудувати дотичну до кола, яка проходить через точку А.

Розв’язування. 1. Аналіз. Нехай задача розв’язана і а – шукана пряма, яка дотикається до кола (О;r) в точці Р (рис. а). Оскільки 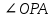прямий, то задача зводиться до побудови точки Р на колі (О;r), з якої відрізки ОА видно під прямим кутом. Відомо, що точка Р лежить на колі, побудованому на відрізку ОА як на діаметрі.

2. Побудова. (рис. 4.1)

  1. Проводимо пряму АО (правило 1).

  2. Будуємо середину М відрізка ОА (побудова 8).

  3. Будуємо коло (М,МА) (правило 2).

  4. Знаходимо точки перетину P і 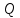кіл (О;r) та (М,МА) (правило 5).

  5. Проводимо прямі АР таAQ (правило 1).

3. Доведення того, що прямі APі AQ – шукані, безпосередньо випливає з побудови. Справді 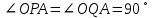, тому AP 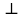OQі AQ 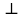OQ. Звідси випливає, що прямі APі AQ– дотичні до кола (О;r).

4. Дослідження. Задача має розв’язки тоді і тільки тоді, коли на даному колі існує точка, з якої відрізок ОА видно під прямим кутом (рис. б), тобто коли кола (О;r) та (М,МА) мають спільні точки. При цьому число розв’язків дорівнює числу спільних точок цих кіл. Можливі два випадки.

1) Точка Aє внутрішньою точкою кола (О;r). Тоді OA ˂ r або 2OM˂ r. Оскільки кола (О;r) та (М,МА) не перетинаються, то задача не має розв’язків.

2) Точка A– є зовнішньою точкою кола (О;r). Тоді OA˃ rабо 2OM˃r. Оскільки кола (О;r) та (М,МА) перетинаються, то задача має два розв’язки.

  1   2   3

скачати

© Усі права захищені
написати до нас