
Міністерство освіти і науки України
Національний технічний університет України
“Київський політехнічний інститут ім. Ігоря Сікорського”
Кафедра ……………………………………………………….
Теорія сучасного управління
«Обчислення перехідної матриці стану методом
Келі-Гамільтона»
Київ-2022
Мета роботи
Вивчити метод обчислення перехідної матриці стану Келі-Гамільтона та набути практичних навиків її обчислення.
Постановка задачі
Знайти власні значення матриці А.
Скласти систему рівнянь, аналогічну (12) для Т= 0,01.
Обчислити перехідну матрицю стану для Т=0,01; 0,1; 0,5; 5.
Хід роботи.
За варіантом, маємо таку перехідну матрицю стану А:
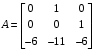
Знайдемо власні значення матриці, розв’язавши її характеристичне рівняння:
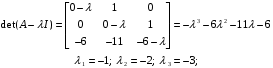
Сформуємо і вирішимо систему алгебраїчних рівнянь згідно з теоремою Келі-Гамільтона:
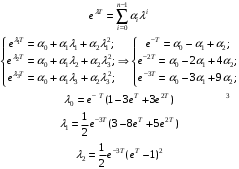
Складемо перехіну матрицю стану:
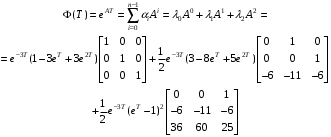
Подальші розрахунки будуть занадто трудомісткими для виконання в ручному режимі, тому напишемо matlab-функцію, що виконає весь розрахунок замість нас:
Лістинг програми:
clc, clear
T = 0.01;
lamb0 = exp(-3 * T) * (1 - 3 * exp(T) + 3 * exp(2 * T));
lamb1 = 0.5 * exp(-3 * T) * (3 - 8 * exp(T) + 5 * exp(2 * T));
lamb2 = 0.5 * exp(-3 * T) * (exp(T) - 1)^2;
A0 = [1 0 0; 0 1 0; 0 0 1];
A1 = [0 1 0; 0 0 1; -6 -11 -6];
A2 = [0 0 1; -6 -11 -6; 36 60 25];
funcT = lamb0 * A0 + lamb1 * A1 + lamb2 * A2;
disp(funcT);
Результати роботи програми:
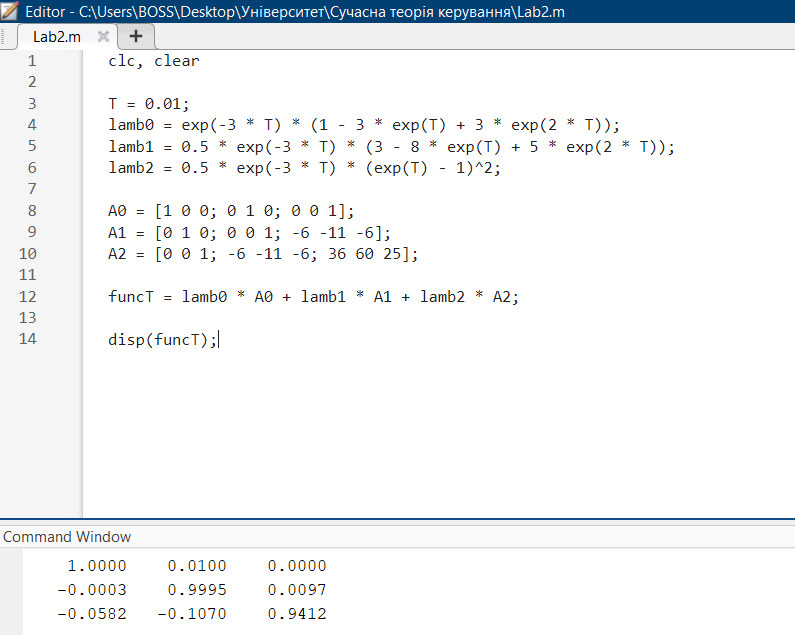
Проведемо обчислення перехідної матриці стану при періодах квантування T=0.01, 0.1, 0.5, 5:
Табл. 1 – Перехідні матриці стану при різних періодах квантування
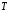 | 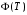 |
| 0.01 | 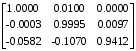 |
| 0.1 | 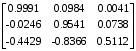 |
| 0.5 | 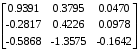 |
| 5 | 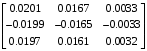 |
Висновок
Під час виконання цієї лабораторної роботи я навчився розраховувати перехідну матрицю стану за допомогою методу Келі-Гамільтона. У порівнянні з методом безпосереднього розкладання в ряд, цей метод є складнішим математично, але при більших порядках об’єкту або більших періодах квантування він буде потребувати набагато менше обчислювальних потужностей. Якщо порівнювати результати обчислення перехідної матриці стану цими двома методами то, як і очікувалося, результати розрахунків є ідентичними.