
Інтергал Рімана

Розіб’ємо
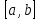 на
на  частин точками
частин точками 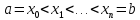
 : Розбиттям
: Розбиттям 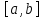 називають сукупність
називають сукупність 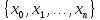 .
. : Сукупність проміжних точок – множина
: Сукупність проміжних точок – множина  , де
, де 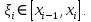
 : Діаметр розбиття -
: Діаметр розбиття - 
 : Інтегральна сума -
: Інтегральна сума -  для функції
для функції  , що побудована за розбиття
, що побудована за розбиття  і сукупністю проміжних точок
і сукупністю проміжних точок 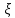 .
. : Інтеграл за Ріманом – число
: Інтеграл за Ріманом – число  нназивають інтегралом за Ріманом від функції
нназивають інтегралом за Ріманом від функції  на
на 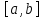 , якщо
, якщо  .
. : Необхідна умова інтегровності – Якщо
: Необхідна умова інтегровності – Якщо  інтегровна за Ріманом, то
інтегровна за Ріманом, то  обмежена на
обмежена на 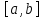 , бо якщо
, бо якщо  необмежена, то
необмежена, то  .
.
Тоді при даному
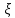

Суми Дарбу.
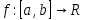 .
. : Верхня сума Дарбу:
: Верхня сума Дарбу:  ,
,  ,
, 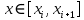 .
. : Нижня сума Дарбу:
: Нижня сума Дарбу:  ,
, 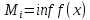 , x
, x 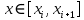 .
.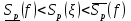
Продовження розбиття.
 цього * сегмента
цього * сегмента 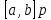 *, де
*, де 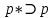
 : Pє спільним для
: Pє спільним для  і
і  , якщо
, якщо  .
. : Інтегральні суми Дарбу та продовжені розбиття.
: Інтегральні суми Дарбу та продовжені розбиття.Якщо
 продовження розбиття, то
продовження розбиття, то  і
і  .
.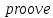 :
: 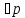 - деяке розбиття,
- деяке розбиття, 

де




 : Нерівність між інтегральними сумами Дарбу.
: Нерівність між інтегральними сумами Дарбу.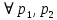 – розбиття
– розбиття 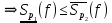

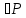 - спільне розбиття:
- спільне розбиття: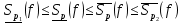
Інтегровність за Дарбу та її зв’язок з інтегровністю за Ріманом
 : Верхній інтеграл Дарбу -
: Верхній інтеграл Дарбу - 
 :Нижній інтеграл Дарбу -
:Нижній інтеграл Дарбу - 
 : Функція
: Функція  називається інтегровною за Дарбу, якщо
називається інтегровною за Дарбу, якщо
 : Критерій інтегровності за Дарбу:
: Критерій інтегровності за Дарбу:  є інтегровною за Дарбу
є інтегровною за Дарбу  .
. (Еквівалентності):
(Еквівалентності): Функція інтегровна за Дарбу
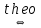 вона інтегровна за Ріманом і їх інтеграли співпадають.
вона інтегровна за Ріманом і їх інтеграли співпадають.Множини лебегової міри нуль
 : Множина
: Множина 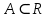 має лебегову міру нуль, якщо
має лебегову міру нуль, якщо  не більш ніж зліченна кількість.
не більш ніж зліченна кількість.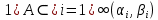
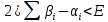
Властивості множин лебегової міри нуль
Якщо
 зліченна або скінченна
зліченна або скінченна  – має міру нуль.
– має міру нуль.Якщо
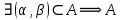 – не є множиною міри нуль.
– не є множиною міри нуль.Незліченна(континуальна) множина теж може мати міру нуль.
Якщо
 мають міру нуль, то і
мають міру нуль, то і 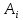 має міру нуль.
має міру нуль. : Критерій Лебега інтегровності за Ріманом.
: Критерій Лебега інтегровності за Ріманом. – обмежена на
– обмежена на 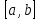 , тоді
, тоді 
 Множина точок розриву функції
Множина точок розриву функції  на
на 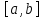 має міру нуль.
має міру нуль.

обмежені







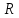
Найпростіші наслідки
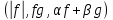
 .
. .
. .
. .
. : Лінійність інтегралу Рімана
: Лінійність інтегралу РіманаЯкщо
 , то
, то 
 : за інтегралом суми.
: за інтегралом суми. : Адитивність за проміжком інтегрування
: Адитивність за проміжком інтегрування
 : Інтеграл Рімана від нерівних функцій
: Інтеграл Рімана від нерівних функцій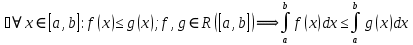
Наслідки
Якщо
 і
і  .
.Інтеграл Рімана.
 :
: 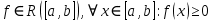
 , то
, то 
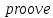 :
: 
Розглянемо
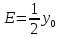 . Тоді
. Тоді 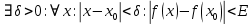 .
.Тобто

 .
.
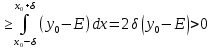
Модуль.
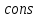 : Якщо
: Якщо  , то
, то  .
.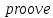 : З пункту 7:
: З пункту 7: 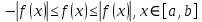
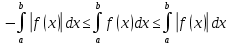
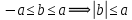
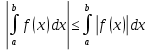
 : Перша про середнє
: Перша про середнє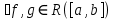 і
і  .
. – не змінює знак на
– не змінює знак на 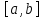

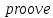 : Будемо вважати, що
: Будемо вважати, що 
Тоді
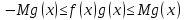
Отже




 : Перша про середнє для неперервної функції
: Перша про середнє для неперервної функціїЯкщо


Інтеграл як функція верхньої межі
 .
.