II часть. ТЕОРЕТИЧЕСКИЕ УПРАЖНЕНИЯ.
1. До показать пользуясь определение, что при
 функция
функция 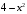 является бесконечно малой.
является бесконечно малой.Функция
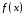 называется бесконечно малой функцией (б. м. ф.) при
называется бесконечно малой функцией (б. м. ф.) при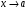 (или в точке
(или в точке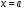 ), если
), если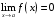 .
.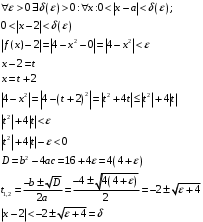
2.
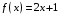
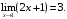 Каково должно быть
Каково должно быть 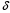 , что бы для
, что бы для 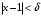 имело место
имело место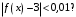
Определение предела
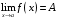
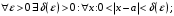
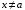 , выполняется неравенство
, выполняется неравенство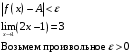
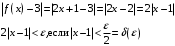
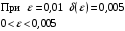
3.
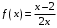
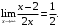 Каково должно быть
Каково должно быть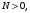 что бы для
что бы для 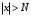 имело место
имело место 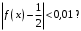
Определение предела
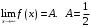
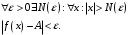
Возьмем произвольным образом
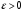
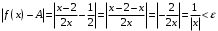
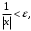 если
если 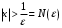
При
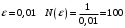
4. Доказать логарифмический признак сходимости рядов: ряд
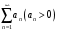 сходится, если существует такое
сходится, если существует такое 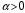 , что
, что 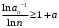 при
при 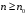 и расходится, если
и расходится, если 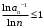 при
при 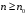 . Можно ли применить логарифмический признак к изучению сходимости ряда
. Можно ли применить логарифмический признак к изучению сходимости ряда 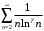 при
при 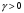 ?
?Логарифмический признак для
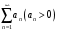 :
:а)
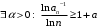 при
при 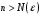
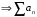 - сходится
- сходитсяДоказательство
при
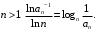
Пусть
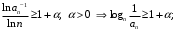
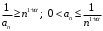 . Ряд
. Ряд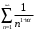 - сходится при
- сходится при 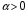
Значит, исходный ряд сходится по I теореме сравнения.
б)
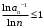 при
при 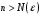
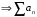 - расходится
- расходится Доказательство
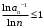
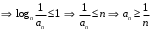
Ряд

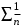 - расходится, значит, исходный ряд тоже расходится (по I теореме сравнения).
- расходится, значит, исходный ряд тоже расходится (по I теореме сравнения). Для ряда
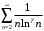 при
при 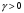 получим:
получим: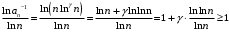 при всех
при всех 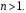 Значит, ряд по логарифмическому признаку, не может расходиться.
Значит, ряд по логарифмическому признаку, не может расходиться. Поскольку
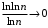 , не существует ни одного
, не существует ни одного 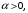 такого, что
такого, что 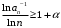 при всех
при всех 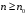 . Значит, первая часть признака не работает. Следовательно, но логарифмическому признаку нельзя сделать вывод сходимости ряда.
. Значит, первая часть признака не работает. Следовательно, но логарифмическому признаку нельзя сделать вывод сходимости ряда. 5. Пусть
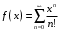 . Доказать непосредственно, что
. Доказать непосредственно, что 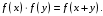
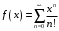
Докажем, что
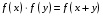
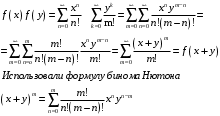
6. Доказать, что ряд
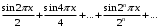 равномерно сходится на всей числовой оси. Показать, что этот ряд нельзя почленно дифференцировать ни на каком интервале.
равномерно сходится на всей числовой оси. Показать, что этот ряд нельзя почленно дифференцировать ни на каком интервале. 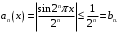
Ряд
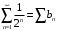 сходится как сумма геометрической прогрессии с
сходится как сумма геометрической прогрессии с 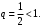 По признаку Вейерштрасса исходный ряд равномерно сходится при всех
По признаку Вейерштрасса исходный ряд равномерно сходится при всех 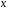 .
. Рассмотрим ряд из производных:
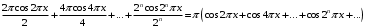 Покажем, что на любом отрезке
Покажем, что на любом отрезке 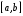 есть точка, в которая
есть точка, в которая 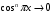
Всегда можно подобрать
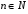 так, что бы на отрезке
так, что бы на отрезке 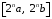 было хотя бы одно целое число
было хотя бы одно целое число 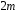 . Положим
. Положим 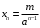 , тогда
, тогда 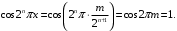 Все остальные слагаемые ряда тоже будут равны 1. Значит, в таких точках для ряда не будет выполнен необходимый признак сходимости
Все остальные слагаемые ряда тоже будут равны 1. Значит, в таких точках для ряда не будет выполнен необходимый признак сходимости 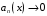 . Значит, исходный ряд нельзя дифференцировать почленно.
. Значит, исходный ряд нельзя дифференцировать почленно. 7. Доказать, что производная от функции
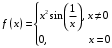
разрывна в точке
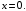
при
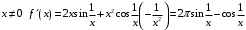
при
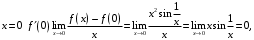
как произведение бесконечно малой функцией не ограниченную.
При этом
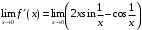 не существует, т. к.
не существует, т. к. 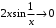 , а
, а 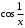 - не имеет предел при
- не имеет предел при 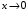 .
.Для доказательства рассмотрим 2 последовательности точек
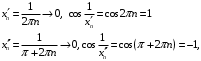
Значит,
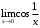 - не существует,
- не существует,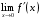 - не существует и
- не существует и 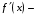 разрывна в
разрывна в 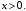
8. Что можно сказать о дифференцируемости суммы
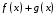 в точке
в точке 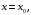 если в этой точке:
если в этой точке:а) функция
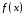 дифференцируема, а функция
дифференцируема, а функция 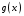 не дифференцируема;
не дифференцируема;б) обе функция
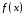 и
и 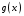 не дифференцируемы.
не дифференцируемы. Теорема. Для того, чтобы функция
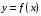 была дифференцируема в точке x , необходимо и достаточно, чтобы она имела конечную производную в этой точке
была дифференцируема в точке x , необходимо и достаточно, чтобы она имела конечную производную в этой точкеПусть
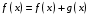
а) Если
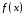 и
и 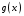 дифференцируема, то
дифференцируема, то 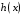 - не дифференцируема, иначе функция
- не дифференцируема, иначе функция 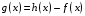 была бы дифференцируема.
была бы дифференцируема. б) Если
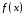 и
и 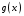 дифференцируема в
дифференцируема в 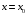 , то
, то 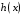 может быть как дифференцируема, так и не дифференцируема
может быть как дифференцируема, так и не дифференцируема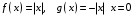 не дифференцируема
не дифференцируема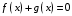 при всех
при всех 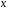 , и дифференцируема в
, и дифференцируема в 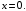
9. Доказать, что функция
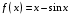 монотонно возрастает на отрезке
монотонно возрастает на отрезкеа)
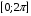 ; б)
; б) 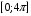 ;
;Следует ли из монотонности дифференцируемой функции монотонность ее производной?
Доказательство
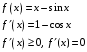
При
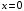 и
и 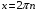
а) Пусть
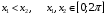
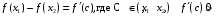
Значит
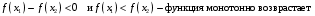
б) Пусть
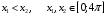
Если
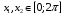 или
или 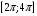 -доказывать как в а);
-доказывать как в а);Если
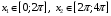
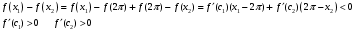 Одно выражение в скобках или оба будут <0.
Одно выражение в скобках или оба будут <0.10.Доказать теорему: если функция
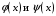 дифференцируемы на отрезке
дифференцируемы на отрезке 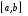 и
и 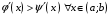 , а
, а 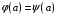 то
то 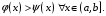
Доказать геометрическую интерпретацию теоремы.
Доказательство
Теорема. Пусть задано на
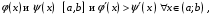
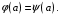 Тогда
Тогда 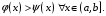
Рассмотрим функцию
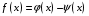 на отрезке
на отрезке 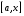 .
. Применим теорему Лагранжа ,где
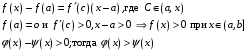

11. Исследовать знаки максимума и минимума функций
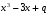 и выяснять условия, при которых уравнение
и выяснять условия, при которых уравнение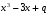 имеет:
имеет:а) Три различных действительных корня
б) Один действительный корень
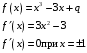
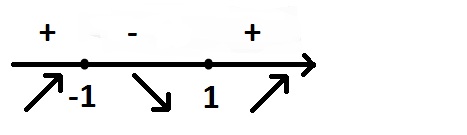
Рисунок 11.1

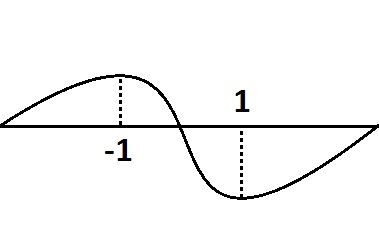
Рисунок 11.2
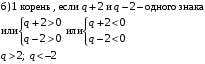
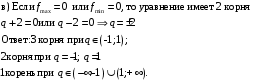
12. Определить «отклонение от нуля» многочлена
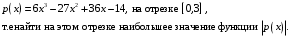
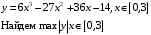
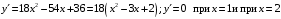
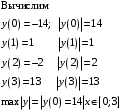
13. Пусть
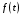 - непрерывная функция, а функции
- непрерывная функция, а функции 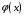 и
и 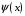
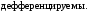 Доказать, что
Доказать, что 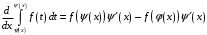
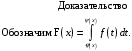
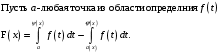
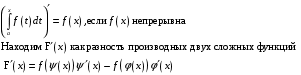
14. Найти точки экстремума функций
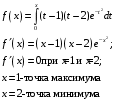
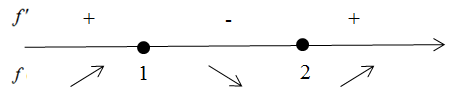
Рисунок 14. 1 точки максимум и минимум
15. Пусть
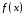 - непрерывная периодическая функция с периодом
- непрерывная периодическая функция с периодом 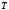 . Доказать, что
. Доказать, что 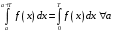
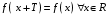
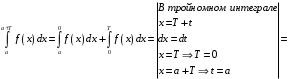
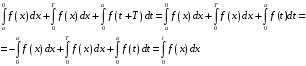
16. При каких целых значений
 интеграл
интеграл 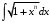 выражается элементарными функциями?
выражается элементарными функциями? 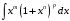 - интеграл Чебышева
- интеграл Чебышева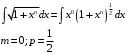
Выражается в элементарных функциях только в случае:
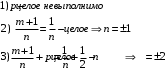
Также
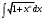 выражается элементарными функциями, если n=0 (в этом случае подынтегральная функция не содержит х)
выражается элементарными функциями, если n=0 (в этом случае подынтегральная функция не содержит х)Ответ:
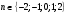
17. Ряды
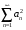 и
и 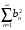 сходится. Доказать, что ряд
сходится. Доказать, что ряд 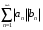 тоже сходится.
тоже сходится. 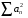 и
и 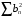 - сходится. Доказать, что
- сходится. Доказать, что 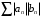 - сходится.
- сходится.Доказательство
Справедливо неравенство
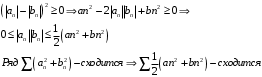
По I теореме сравнения ряд
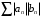
18. Показать, что функция
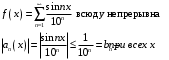
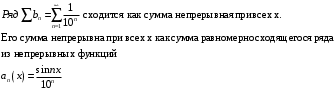
19. Может ли функциональный ряд на отрезке
а) сходится равномерно и не сходится абсолютно,
б) сходится абсолютно и не сходится равномерно?
Рассмотреть примеры:
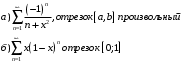
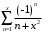 - покажем, что сходится равномерно, но не абсолютно.
- покажем, что сходится равномерно, но не абсолютно. Признак Дирихле равномерной сходимости рядов:
Пусть частичные суммы ряда
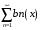 при любых
при любых  и
и  ограниченны, а последовательность функций
ограниченны, а последовательность функций 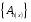 - монотонно и равномерно сходится к области
- монотонно и равномерно сходится к области 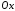 .
.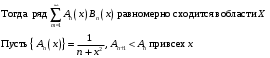
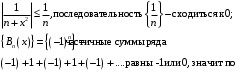
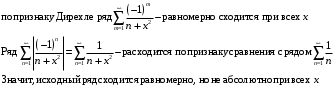

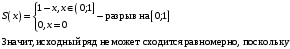

20. Доказать, что