Ім'я файлу: Статистика.docx
Розширення: docx
Розмір: 165кб.
Дата: 17.05.2021
скачати
Пов'язані файли:
мой диплом)).pdf

1.

1) Комбінаційне групування здійснюється за двома ознаками: обсяг капіталу банків та їх прибуток. Це дає комбінаційний ряд розподілу з неперервними ознаками, варіації яких незначні. Застосувавши рівні інтервали, визначимо їх ширину і сформуємо інтервали.

Для обсягу капіталу:

інтервали 3-6. 6-9, 9-12.

Для прибудку:

інтервали <4,8; 4,8-7,2;≥7,2. 

2) Для підтвердження наявності зв’язку між обсягом капіталу (факторна ознака) та прибутком (результативна ознака) використовується аналітичне групування.


Обсяг капіталу
Прибуток млн, грн, разом
На 1 банк

3-6
27,3
3,0

6-9
68,5
5,3

9-12
65,3
8,2

Всього
161,1
x

В середньому
53,7
5,5

Зіставлення групових значень факторної та результативної ознак показує, що прямий зв’язок між ознаками дає змогу визначити інтенсивність змін результативної ознаки. За умови збільшення обсягу капіталу різниця між групами середнього прибутку на один банк зростає, що характеризує збільшення впливу факторної ознаки (обсяг капіталу) на результативну ознаку: прибуток для другої групи – (5,3-3,0)=2,3млн.грн; для третьої групи – (8,2-5,3)=2,9млн.грн.
2.

1) Розмах варіації складає 8 тис. грн

2) Dx=∑i=1n(xi−mx)2pi
Математичне очікування в п.1 xi;pi берем

Dx=(11−13)16∗0.15+(4.2−6.38)2∗0.18+(16−19)2∗0.3+

+(8.5−6.38)2∗0.21+(10.4−6.38)2∗0.16=6.9054

3.

Введемо вектор обсягу споживчих товарів ⃗=(3;10;2); вектор цін у поточному місяці с⃗ ( ); вектор цін у попередньому місяці  (3500;1800;4500). n с Розрахуємо індекс цін. Для цього обчислимо скалярні добутки c  q та c q n  c  q  3 4000 10 2000  2 4000  40000 ; c  q  33500 101800  2 4500  37500; n Тепер перейдемо до індексу інфляції. p  40000 : 37500100 % 106,7 %. А також i  p 100 % 106,7 % 100 %  6,7 %. Таким чином, індекс інфляції становить 6,7%
4.

 ― ймовірність того, що виріб якісний, якщо він з першої партії;

 ― ймовірність того, що виріб якісний, якщо він з другої партії.

Ймовірності того, що вироби браковані, відповідно дорівнюють:   .

а) подія   ― серед двох виробів хоча б один бракований;

протилежна подія   ― обидва вироби якісні, тоді

 .

б) подія   ― обидва вироби браковані:

 .

в) подія   ― один виріб бракований і один якісний:

 .

5.


n = 1 + 3,322log n = 1 + 3,322log(50) = 7
Ширина інтервала складає:

xmax - максимальне значення групувальної ознаки в сукупності

xmin - мінімальне значення групувальної ознаки.

Визначимо межі групи.

Номер групи
Нижня межа
Верхня межа

1
120
131

2
131
142

3
142
153

4
153
164

5
164
175

6
175
186

7
186
200


Одне і теж значення ознаки служить верхньою і нижньою межами двох суміжних (попередньої і наступної) груп.

Для кожного значення ряду підрахуємо, яка кількість разів воно потрапляє в той чи інший інтервал. Для цього сортуємо ряд по зростанню.

120
120 − 131
1

122
120 − 131
2

131
131 − 142
1

133
131 − 142
2

134
131 − 142
3

138
131 − 142
4

140
131 − 142
5

142
142 − 153
1

145
142 − 153
2

147
142 − 153
3

147
142 − 153
4

148
142 − 153
5

148
142 − 153
6

150
142 − 153
7

150
142 − 153
8

152
142 − 153
9

152
142 − 153
10

153
153 − 164
1

156
153 − 164
2

158
153 − 164
3

158
153 − 164
4

159
153 − 164
5

160
153 − 164
6

160
153 − 164
7

160
153 − 164
8

160
153 − 164
9

161
153 − 164
10

164
164 − 175
1

165
164 − 175
2

165
164 − 175
3

167
164 − 175
4

168
164 − 175
5

169
164 − 175
6

170
164 − 175
7

170
164 − 175
8

170
164 − 175
9

172
164 − 175
10

173
164 − 175
11

174
164 − 175
12

176
175 − 186
1

178
175 − 186
2

180
175 − 186
3

180
175 − 186
4

182
175 − 186
5

184
175 − 186
6

190
186 − 197
1

194
186 − 197
2

196
186 − 197
3

198
186 − 197
4

200
186 − 197
5


Результати угруповання оформимо у вигляді таблиці:

Групи
№

Частота fi

120 − 131
6,3
2

131 − 142
49,46,40,35,9
5

142 − 153
39,47,25,34,38,48,4,50,2,13
10

153 − 164
17,32,36,42,24,5,7,10,37,45
10

164 − 175
16,11,27,23,33,26,8,31,41,14,22,44
12

175 − 186
18,28,1,12,19,29
6

186 − 197
30,20,43,21,15
5


Таблиця для розрахунку показників.

Групи
Середина інтервалу, xцентр
Кол-во, fi
xi·fi
Накопичена частота, S
|x-xср|·fi
(x-xср)2·fi
частота, fi/f

120 - 131
125.5
2
251
2
72.02
2593.44
0.04

131 - 142
136.5
5
682.5
7
125.05
3127.501
0.1

142 - 153
147.5
10
1475
17
140.1
1962.801
0.2

153 - 164
158.5
10
1585
27
30.1
90.601
0.2

164 - 175
169.5
12
2034
39
95.88
766.081
0.24

175 - 186
180.5
6
1083
45
113.94
2163.721
0.12

186 - 200
193
5
965
50
157.45
4958.101
0.1

Итого



50
8075.5



734.54
15662.245
1


Для оцінки ряду розподілу знайдемо наступні показники:

Показники центру розподілу.

Середня зважена (вибіркова Середня)

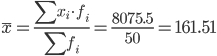
Мода.
Мода - найбільш часто зустрічається значення ознаки у одиниць даної сукупності.
де x0 – початок модального інтервалу; h –величина інтервалу; f2 – частота, відповідна модальному інтервалу; f1 – предмодальная частота; f3-послемодальная частота.

Вибираємо в якості початку інтервалу 164, так як саме на цей інтервал припадає найбільша кількість.
Наиболее часто встречающееся значение ряда – 166.75
Медіана.

Медіана ділить вибірку на дві частини: половина варіант менше медіани, половина — більше.

Медіана служить хорошою характеристикою при асиметричному розподілі даних, тому що навіть при наявності "викидів" даних, медіана більш стійка до впливу відхиляються даних.

В інтервальному ряду розподілу відразу можна вказати тільки інтервал, в якому будуть знаходитися мода або медіана. Медіана відповідає варіанту, що стоїть в середині ранжируваного ряду. Медіанним є інтервал 164-175, тому що в цьому інтервалі накопичена частота S, більше медіанного номера (медіанним називається перший інтервал, накопичена частота S якого перевищує половину загальної суми частот).


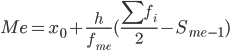
Таким чином, 50% одиниць сукупності будуть менше за величиною 161.8.

У симетричних рядах розподілу значення моди і медіани збігаються з середньою величиною (хср=Me=Mo), а в помірно асиметричних вони співвідносяться таким чином: 3 (хср-Me) ∙ хср-Mo

Середнє значення досліджуваного ознаки за способом моментів.

де а – умовний нуль, рівний варіанті з максимальною частотою (середина інтервалу з максимальною частотою), h-крок інтервалу.

Знаходимо А = 169.5

Крок інтервалу h = 11

Середній квадрат відхилень за способом моментів.


xц
x*i
fi
x*ifi
[x*i]2fi

125.5
-4
2
-8
32

136.5
-3
5
-15
45

147.5
-2
10
-20
40

158.5
-1
10
-10
10

169.5
0
12
0
0

180.5
1
6
6
6

193
2.1
5
10.5
22.05







50
-36.5
155.05




Среднее квадратическое отклонение.

Показатели вариации.
Абсолютные показатели вариации.
Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда.
R = xmax - xmin = 200 - 120 = 80
Среднее линейное отклонение - вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности.

Каждое значение ряда отличается от другого в среднем на 14.691
Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).

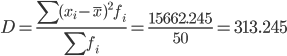
Несмещенная оценка дисперсии - состоятельная оценка дисперсии (исправленная дисперсия).

Среднее квадратическое отклонение.

Каждое значение ряда отличается от среднего значения 161.51 в среднем на 17.699
Оценка среднеквадратического отклонения.

Відносні показники варіації.

До відносних показників варіації відносять: коефіцієнт осциляції, лінійний коефіцієнт варіації, відносне лінійне відхилення.
Коэффициент вариации - мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс.

Поскольку v ≤ 30%, то совокупность однородна, а вариация слабая. Полученным результатам можно доверять.
Линейный коэффициент вариации или Относительное линейное отклонение - характеризует долю усредненного значения признака абсолютных отклонений от средней величины.

Коэффициент осцилляции - отражает относительную колеблемость крайних значений признака вокруг средней.

Доверительный интервал для дисперсии.
Вероятность выхода за нижнюю границу равна P(χ2n-1 < hH) = (1-γ)/2 = (1-0.954)/2 = 0.023. Для количества степеней свободы k = 49 по таблице распределения χ2 находим:
χ2(49;0.023) = 37.68865.
Случайная ошибка дисперсии нижней границы:


Вероятность выхода за верхнюю границу равна P(χ2n-1 ≥ hB) = 1 - P(χ2n-1 < hH) = 1 - 0.023 = 0.977. Для количества степеней свободы k = 49, по таблице распределения χ2 находим:
χ2(49;0.977) = 37.68865.
Случайная ошибка дисперсии верхней границы:


Таким чином, інтервал (415.57; 415.57) покриває параметр S2 з надійністю γ = 0.954

Довірчий інтервал для середньоквадратичного відхилення.

S(1-q) < σ < S(1+q)

Знайдемо довірчий інтервал для середньоквадратичного відхилення з надійністю γ = 0.954 і обсягом вибірки n = 50

По таблиці q=q (γ ; n) визначаємо параметр q (0.954;50) =

17.878(1-) < σ < 17.878(1+)

17.878 < σ < 17.878

Таким чином, інтервал (17.878;17.878) покриває параметр σ з надійністю γ = 0.954

Перевірка гіпотез про вид розподілу.

1. Перевіримо гіпотезу про те, що Х розподілено за нормальним законом за допомогою критерію згоди Пірсона.

де pi-ймовірність потрапляння в i-й інтервал випадкової величини, розподіленої за гіпотетичним законом

Для обчислення ймовірностей pi застосуємо формулу і таблицю функції Лапласа

где
s = 17.699, xср = 161.51
Теоретична (очікувана) частота дорівнює fi = fpi, де f = 50

Імовірність попадання в i-й інтервал: pi = Ф (x2) - Ф ( x1)

xi÷xi+1
fi
x1 = (xi - xср)/s
x2 = (xi+1 - xср)/s
Ф(x1)
Ф(x2)
pi=Ф(x2)-Ф(x1)
Ожидаемая частота, 50pi
Слагаемые статистики Пирсона, Ki

120 - 131
2
-2.3218
-1.7065
-0.4904
-0.4564
0.034
1.7
0.05294

131 - 142
5
-1.7065
-1.0913
-0.4564
-0.3643
0.0921
4.605
0.03388

142 - 153
10
-1.0913
-0.476
-0.3643
-0.1844
0.1799
8.995
0.1123

153 - 164
10
-0.476
0.1393
-0.1844
0.0557
0.2401
12.005
0.3349

164 - 175
12
0.1393
0.7545
0.0557
0.2764
0.2207
11.035
0.08439

175 - 186
6
0.7545
1.3698
0.2764
0.4147
0.1383
6.915
0.1211

186 - 200
5
1.3698
2.1529
0.4147
0.4846
0.0699
3.495
0.6481




50


















1.3875


Визначимо межу критичної області. Так як статистика Пірсона вимірює різницю між емпіричним і теоретичним розподілами, то чим більше її спостережуване значення Кнабл, тим сильніше аргумент проти основної гіпотези.

Тому критична область для цієї статистики завжди правостороння: [Kkp;+∞).

Її кордон Kkp = χ2 (k-r-1;α) знаходимо за таблицями розподілу χ2 і заданими значеннями s, k (число інтервалів), r=2 (параметри xcp і s оцінені за вибіркою).

Kkp = χ2 (7-2-1;0.05) = 9.48773; Кнабл = 1.39

Спостережуване значення статистики Пірсона не потрапляє в критичну область: Кнабл < Kkp, тому немає підстав відкидати основну гіпотезу. Справедливо припущення про те, що дані вибірки мають нормальний розподіл.

Висновок:

Кожне значення ряду відрізняється від середнього значення 161.51 в середньому на 17.699.

Середнє значення приблизно дорівнює моді і медіані, що свідчить про нормальний розподіл вибірки.

Оскільки коефіцієнт варіації менше 30%, то сукупність однорідна. Отриманим результатам можна довіряти.

Перевірка гіпотези за критерієм згоди Пірсона показала, що немає підстав відкидати гіпотезу про нормальний закон розподілу.

6.

Зведений індекс цін визначається за формулою:  

Значення цін у листопаді за умовою завдання не відомі, проте відома їх зміна. Висловимо з формули індивідуального індексу значення ціни за листопад:

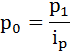
Перетворимо формулу індексу цін:



Ціни зросли на 4 %.

Індекс товарообігу визначається за формулою:





Індекс фізичного обсягу продукції:



Перетворимо формулу індексу фізичного обсягу:





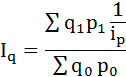
Можна скористатися взаємозв'язком трьох індексів:





Відповідь:

Ціни в цілому зросли на 4 %.

Товарообіг зменшився на 19,6%.

Фізичний обсяг зменшився на 22,2%.
скачати

© Усі права захищені
написати до нас