
Ім'я файлу: 94507.docx
Розширення: docx
Розмір: 799кб.
Дата: 24.11.2020
скачати
Пов'язані файли:
Сферична геометрія.docx
Розширення: docx
Розмір: 799кб.
Дата: 24.11.2020
скачати
Пов'язані файли:
Сферична геометрія.docx
.
Автор - упорядник:
Михальчук Оксана Олександрівна, вчитель, Ізюмська загальноосвітня школа І-ІІІ ступенів
№ 11 Ізюмської міської ради Харківської області, спеціаліст вищої категорії.
Діофантові рівняння.
Дана робота – спроба розробити серію факультативних занять із математики для учнів 6-9 класів за темою « Діофантові рівняння», які містять різнорівневі завдання з теми і ознайомлять дітей із основними способами розв’язання таких рівнянь . Задачі, які зводяться до розв’язання діофантових рівнянь, часто зустрічаються на олімпіадах різних рівнів і є однією з найулюбленіших тем у теоретико-числових дослідженнях математиків. Розв’язання діофантових рівнянь сприяє розвитку теоретичного та логічного мислення школярів.
Робота призначена для вчителів математики середніх і старших класів.
Зміст.

Вступ…………………………….…………………………………………………..4
Математичні основи розв’язування діофантових рівнянь………………….…6
1.1.Рівняння першого степеня з двома невідомими……………………………….6
1.2. Рівняння другого степеня………………………………………………………7
1.2.1. Приклад розв’язування рівняння другого степеня з трьома невідомими…7
1.2.2. Рівняння другого степеня з двома невідомими……………………………..9
1.3. Рівняння з двома невідомими степеня вище другого……………………...…9
2. Методика підготовки учнів до розв’язання олімпіадних задач, пов’язаних із діофантовими рівняннями………………………………..…………………..10
2.1. Принципи відбору теоретичного матеріалу………………………………..10
2.2. Найпростіші методи розв’язування діофантових рівнянь………………….11
3. Додатки…………………………………………………………………………...11
3.1. Розробки факультативних занять за темою «Діофантові рівняння»….…..11
3.1.1. Заняття № 1……………………………………………………………….….11
3.1.2. Заняття № 2…………………………………………………………………..14
3.1.3. Заняття № 3……………………………………………………………….….18
3.1.4. Заняття № 4………………………………………………………………..…20
3.1.5. Заняття № 5………………………………………………………………....24
3.1.6. Заняття № 6………………………………………………………………….29
Висновки……………………………………………………………………………33
Література………………………………………………………………………….34
Вступ.
Теорія чисел вивчає насамперед арифметичні властивості чисел натурального ряду, іншими словами, цілих додатних чисел, і належить до старовинних розділів математики. Однією із центральних задач так званої аналітичної теорії чисел є задача про розподіл простих чисел у натуральному ряду. Простим числом називається будь – яке ціле додатне число, більше одиниці, що поділяється тільки на себе і одиницю. Задача про розподіл простих чисел у натуральному ряду полягає у вивченні правильності поведінки кількості простих чисел, менших деякого числа
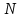 , при великих значеннях
, при великих значеннях 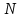 . Перший результат у цьому напрямку ми знаходимо ще у Евкліда (
. Перший результат у цьому напрямку ми знаходимо ще у Евкліда ( ст. до н.е.), саме доведення нескінченності ряду простих чисел; другий результат після Евкліда був отриманий видатним російським математиком П.Л.Чебишевим у другій половині
ст. до н.е.), саме доведення нескінченності ряду простих чисел; другий результат після Евкліда був отриманий видатним російським математиком П.Л.Чебишевим у другій половині ст. Інша основна задача теорії чисел - це задача про подачу цілих чисел у вигляді суми цілих чисел певного типу, наприклад, проблема подачі непарних чисел у вигляді суми трьох простих чисел, яка була розв’язана сучасним представником теорії чисел - радянським математиком І.М.Віноградовим .
ст. Інша основна задача теорії чисел - це задача про подачу цілих чисел у вигляді суми цілих чисел певного типу, наприклад, проблема подачі непарних чисел у вигляді суми трьох простих чисел, яка була розв’язана сучасним представником теорії чисел - радянським математиком І.М.Віноградовим .Дана робота присвячена одному із найбільш цікавих розділів теорії чисел, а саме - розв’язуванню рівнянь у цілих числах або діофантових рівнянь.
Розв’язок у цілих числах алгебраїчних рівнянь з цілими коефіцієнтами більш ніж із одним невідомим являє собою одну із складніших проблем теорії чисел. Цими задачами багато займались самі видатні математики давнини: грецький математик Піфагор (
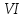 ст. до н.е. ); кращі математики більш близької до нас доби –П.Ферма (
ст. до н.е. ); кращі математики більш близької до нас доби –П.Ферма (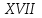 ст.), Л.Ейлер (
ст.), Л.Ейлер (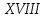 ст. ), Ж.Л.Лагранж (
ст. ), Ж.Л.Лагранж ( 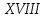 ст.) та інші.
ст.) та інші.Одним із математиків, що займались цією проблемою, був давньогрецький математик Діофант Олександрійський, праці якого мали велике значення для алгебри та теорії чисел. До нашого часу не з’ясовані ні рік народження, ні дата смерті Діофанта ; вважають, що він жив у
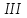 ст. н.е. В одному із давніх рукописних збірників задач у віршах життя Діофанта описується у вигляді наступної алгебраїчної загадки, що являє собою надпис на його могилі:
ст. н.е. В одному із давніх рукописних збірників задач у віршах життя Діофанта описується у вигляді наступної алгебраїчної загадки, що являє собою надпис на його могилі:Прах Диофанта гробница покоит; дивись ей – камень,
Мудрым искусством его скажет усопшего век.
Волей богов шестую часть жизни он прожил ребенком.
И половину шестой встретил с пушком на щеках.
Только минула седьмая, с подругой он обручился.
С нею, пять лет проведя, сына дождался мудрец;
Только полжизни отцовской возлюбленный сын его прожил.
Отнят он был у отца ранней могилой своей.
Дважды два года родитель оплакивал тяжкое горе,
Тут и увидел предел жизни печальной своей.
Задача – загадка зводиться до складання і розв’язування рівняння:
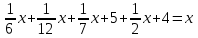 ,
,звідки
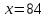 - ось скільки років жив Діофант.
- ось скільки років жив Діофант.Із робіт Діофанта найважливішою є „Арифметика”, з 13 книг якої тільки 6 збереглися до наших днів. Ці книги були відкриті у Венеції у 1463 р. Регіомонтаном, котрий у зв’язку з цим писав, що у праці Діофанта зосереджено „увесь колір арифметики, мистецтва невідомої”.
У збережених книгах Діофанта міститься 189 задач із розв’язанням. У першій книзі викладені задачі, що зводяться до визначених рівнянь першого та другого степенів. Інші п’ять книг містять в основному невизначені рівняння. У цих книгах ще нема систематичної теорії невизначених рівнянь, методи розв’язування змінюються від випадку до випадку. Діофант задовольняється будь – яким одним розв’язком, цілим або дробовим, аби він було додатнім.
Методи розв’язання невизначених рівнянь складають основний вклад Діофанта у математику. Відомо, що у символіці Діофанта був один тільки знак для невідомого. Розв’язуючи невизначене рівняння, він використовував у якості декількох невідомих довільні числа, замість яких можна було взяти і будь – які інші, що і зберігало характер загальності його розв’язку .
Не дивлячись на зусилля багатьох поколінь видатних математиків, у цій області відсутні загальні методи. Проблема розв’язування рівнянь у цілих числах вирішена до кінця тільки для рівнянь другого степеня з двома невідомими. Слід зазначити, що для рівнянь будь – якого степеня з одним невідомим вона не представляє суттєвого інтересу, бо ця задача може бути розв’язана за допомогою кінцевого числа спроб. Для рівнянь вищих степенів із двома та більше невідомими дуже складна не тільки задача знаходження усіх розв’язків у цілих числах, але і більш проста задача встановлення існування кінцевої або нескінченної множини таких розв’язків.
Розв’язання рівнянь у цілих числах має не тільки теоретичний інтерес. Такі рівняння іноді зустрічаються у фізиці та практиці людини. Крім того діофантові рівняння і задачі, які зводяться до діофантових рівнянь досить часто зустрічаються в завданнях математичних олімпіад різних рівнів . Оскільки діофантові рівняння не вивчаються в основному курсі математики в школі, доцільно організовувати знайомство учнів з основними ідеями, пов’язаними з діофантовими рівняннями, на факультативних заняттях.
Тому, метою роботи було розробити серію факультативних занять, на яких учні зможуть оволодіти методами розв’язування олімпіадних задач, пов’язаних із діофантовими рівняннями. Для досягнення цієї мети було поставлено такі завдання:
проаналізувати математичні основи теорії діофантових рівнянь і відібрати теоретичний матеріал, з яким доцільно познайомити учнів;
виділити основні методи розв’язування задач, пов’язаних із діофантовими рівняннями;
підібрати різнорівневу систему завдань для відпрацювання кожного методу;
розробити систему занять по ознайомленню учнів із завданнями, які зводяться до діофантових рівнянь і розробити методичні рекомендації по проведенню цих занять.
1. Математичні основи розв’язування діофантових рівнянь.
1.1. Рівняння першого степеня з двома невідомими.
Спочатку розглянемо рівняння першого степеня з одним невідомим
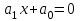 (1)
(1)Нехай коефіцієнти рівняння
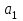 та
та 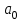 – цілі числа. Зрозуміло, що розв’язок цього рівняння
– цілі числа. Зрозуміло, що розв’язок цього рівняння 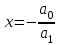 буде цілим числом тільки в тому випадку, коли
буде цілим числом тільки в тому випадку, коли 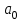 буде ділитись на
буде ділитись на 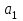 без залишку. Таким чином, рівняння (1) не завжди має розв’язки у цілих числах.
без залишку. Таким чином, рівняння (1) не завжди має розв’язки у цілих числах.Так само і рівняння, степінь яких вище одиниці. Але питання про знаходження цілих коренів рівняння n-го степеня з цілими коефіцієнтами
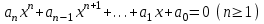 (2)
(2)розв’язується легко.
Дійсно, нехай
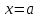 – цілий корінь цього рівняння.
– цілий корінь цього рівняння. Тоді
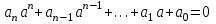 ,
, 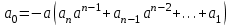 .
.З останньої рівності видно , що а0 ділиться на а без залишку ; отже, кожний цілий корінь рівняння (2) є дільником вільного вільного члена рівняння. Для знаходження цілих розв’язків рівняння треба вибрати ті з дільників
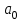 , котрі при підстановці у рівняння перетворюють його у тотожність.
, котрі при підстановці у рівняння перетворюють його у тотожність.Значно більший інтерес являє розв’язання у цілих числах рівнянь з багатьма невідомими.
Отже, розглянемо рівняння першого степеня з двома невідомими
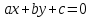 , (3)
, (3)де
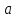 і
і 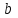 - цілі числа, відмінні від нуля, а
- цілі числа, відмінні від нуля, а 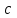 - довільне ціле. Будемо вважати, що коефіцієнти
- довільне ціле. Будемо вважати, що коефіцієнти 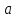 та
та 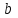 не мають спільних дільників, крім одиниці. Дійсно, якщо найбільший спільний дільник цих коефіцієнтів
не мають спільних дільників, крім одиниці. Дійсно, якщо найбільший спільний дільник цих коефіцієнтів 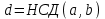 відмінний від одиниці, то справджуються рівності
відмінний від одиниці, то справджуються рівності 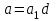 ,
, 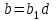 ; рівняння (3) приймає вигляд
; рівняння (3) приймає вигляд 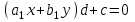 і має мати цілі розв’язки тільки в тому випадку, коли
і має мати цілі розв’язки тільки в тому випадку, коли 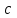 ділиться на
ділиться на 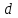 . Таким чином, у випадку
. Таким чином, у випадку 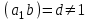 усі коефіцієнти рівняння (3) повинні ділитись на
усі коефіцієнти рівняння (3) повинні ділитись на 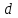 без залишку, і, скоротивши (3) на
без залишку, і, скоротивши (3) на 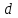 , прийдемо до рівняння
, прийдемо до рівняння 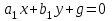 ,
,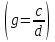 , коефіцієнти якого
, коефіцієнти якого 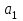 та
та 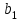 взаємно прості.
взаємно прості.Розглянемо спочатку випадок, коли
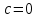 . Рівняння (3) матиме вигляд:
. Рівняння (3) матиме вигляд: 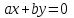 (3’).
(3’).Розв’язуючи це рівняння відносно
 , отримаємо
, отримаємо 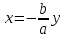 . Зрозуміло, що
. Зрозуміло, що  буде приймати цілі значення лише в тому випадку, коли
буде приймати цілі значення лише в тому випадку, коли  ділиться на
ділиться на 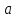 без остачі. Але будь-яке ціле
без остачі. Але будь-яке ціле  , що кратне
, що кратне 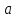 , можна записати у вигляді:
, можна записати у вигляді: 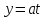 , де
, де 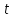 приймає довільні цілі значення
приймає довільні цілі значення 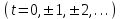 . Підставимо це значення
. Підставимо це значення  у попереднє рівняння , тоді
у попереднє рівняння , тоді 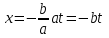 , і ми отримаємо формули, що містять всі цілі розв’язки рівняння (3’) :
, і ми отримаємо формули, що містять всі цілі розв’язки рівняння (3’) :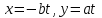
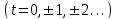 .
. Перейдемо до випадку
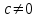 . Для знаходження всіх цілих розв’язків рівняння (3) достатньо знайти будь-який один його розв’язок , тобто знайти такі цілі числа
. Для знаходження всіх цілих розв’язків рівняння (3) достатньо знайти будь-який один його розв’язок , тобто знайти такі цілі числа 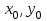 , для яких
, для яких  .
.Теорема I. (без доведення) Нехай
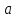 і
і 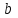 взаємно прості і
взаємно прості і 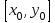 - будь-який розв’язок рівняння
- будь-який розв’язок рівняння 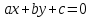 (3). Тоді формули
(3). Тоді формули 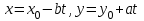 (4) при
(4) при 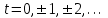 дають усі розв’язки рівняння (3).
дають усі розв’язки рівняння (3). 1.2.Рівняння другого степеня.
1.2.1. Приклад розв’язування рівняння другого степеня з трьома невідомими.
Приклад. Розглянемо рівняння другого степеня з трьома невідомими:
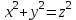 (5)
(5) Геометрично розв’язок цього рівняння у цілих числах можна подати як знаходження всіх піфагорових трикутників, тобто прямокутних трикутників, у яких катети
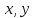 і гіпотенуза
і гіпотенуза 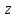 виражені цілими числами.
виражені цілими числами.Позначимо через
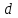 найбільший спільний дільник чисел
найбільший спільний дільник чисел  та
та  :
: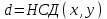 . Тоді
. Тоді 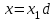 ,
,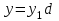 і рівняння (5) прийме вигляд
і рівняння (5) прийме вигляд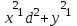
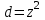
Звідси випливає, що
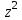 ділиться на
ділиться на 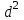 і, значить
і, значить 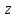 кратне
кратне 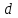 :
: 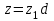
Тепер рівняння (5) можна записати у вигляді
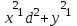
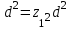
Скоротивши на
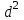 , одержимо
, одержимо 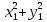 =
=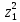 .
.Ми прийшли до рівняння того ж виду, що і початкове, причому тепер величини
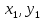 не мають спільних дільників, крім 1. Таким чином, при розв’язанні рівняння (5) можна обмежитись випадком, коли
не мають спільних дільників, крім 1. Таким чином, при розв’язанні рівняння (5) можна обмежитись випадком, коли 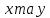 взаємно прості. Отже, нехай НСД
взаємно прості. Отже, нехай НСД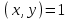 . Тоді, хоча б одна з величин
. Тоді, хоча б одна з величин  та
та  (наприклад,
(наприклад,  ) буде непарною.
) буде непарною.Перенесемо
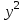 у праву частину рівняння (5), отримаємо
у праву частину рівняння (5), отримаємо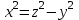 ;
; 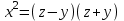 (6)
(6)Позначимо через
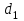 найбільший спільний дільник виразів
найбільший спільний дільник виразів 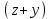 та
та 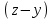 , тоді
, тоді 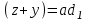 ,
, 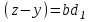 , (7)
, (7)де
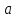 і
і 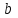 взаємно прості.
взаємно прості.Підставляючи в (6) значення
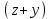 та
та 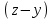 , отримаємо
, отримаємо 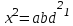 . Так як числа
. Так як числа 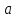 і
і 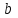 не мають спільних дільників, то одержана рівність можлива лише у випадку , коли
не мають спільних дільників, то одержана рівність можлива лише у випадку , коли 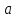 і
і 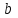 будуть повними квадратами:
будуть повними квадратами: 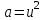 ,
,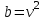
Але тоді
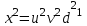 і тоді
і тоді 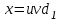 (8)
(8)Знайдемо тепер
 та
та 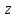 із рівностей (7) . Додавання цих рівностей дає
із рівностей (7) . Додавання цих рівностей дає 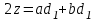
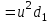
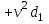 ;
; 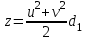 (9)
(9)Віднімаючи другу рівність (7) від першої отримаємо
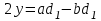
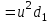
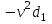 ;
; 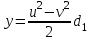 (10)
(10)В силу непарності
 із (15) маємо, що
із (15) маємо, що 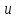 і
і 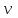 також непарні. Більш того,
також непарні. Більш того, 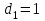 так як інакше з рівностей
так як інакше з рівностей 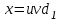 та
та 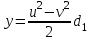 випливало б, що величини
випливало б, що величини  та
та  мають спільний дільник
мають спільний дільник 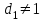 , що суперечить припущенню про їх взаємну простоту. Числа
, що суперечить припущенню про їх взаємну простоту. Числа 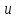 та
та 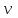 пов’язані із взаємно простими числами та рівностями і в силу цього самі взаємно прості;
пов’язані із взаємно простими числами та рівностями і в силу цього самі взаємно прості;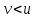 ,бо
,бо 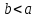 ,що зрозуміло із рівностей (7).
,що зрозуміло із рівностей (7).Підставляючи у рівності (8) – (10)
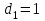 ,отримаємо формули:
,отримаємо формули: 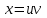 ,
, 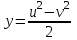 ,
, 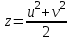 , (11)
, (11) що дають при непарних взаємно простих
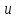 та
та 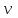 усі вільні від спільних дільників трійки цілих додатних чисел
усі вільні від спільних дільників трійки цілих додатних чисел  , що задовольняють рівнянню (5) . Простою підстановкою
, що задовольняють рівнянню (5) . Простою підстановкою 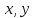 та
та 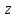 у рівняння (5) легко перевірити, що при будь- яких
у рівняння (5) легко перевірити, що при будь- яких 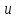 та
та 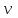 числа (11) задовольняють цьому рівнянню.
числа (11) задовольняють цьому рівнянню.Звідси випливають рівності, які часто зустрічаються:
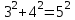 (
(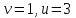 ),
), (
(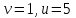 ),
), (
(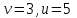 ).
).Як вже було сказано, формули (11) дають тільки ті розв’язки рівняння
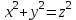 , в яких числа
, в яких числа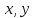 та
та 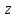 не мають спільних дільників. Всі інші цілі додатні розв’язки цього рівняння можна отримати, якщо помножити розв’язки, що містяться у формулах (11), на довільний спільний множник
не мають спільних дільників. Всі інші цілі додатні розв’язки цього рівняння можна отримати, якщо помножити розв’язки, що містяться у формулах (11), на довільний спільний множник 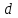 .
.Тим самим шляхом , яким ми одержали усі розв’язки рівняння (5), можуть бути одержані і всі розв’язки інших рівнянь того ж типу.
1 2 3 4 5