Активний опір у колі змінного (синусоїдного) струму
Якщо на синусоїдну напругу увімкнути резистивний елемент, тобто
,то у колі виникне так званий миттєвий струм
.Таким чином можна зробити висновок, що струм у колі з активним опором, увімкнутим на синусоїдну напругу, є синусоїдним та збігається з напругою за фазою.
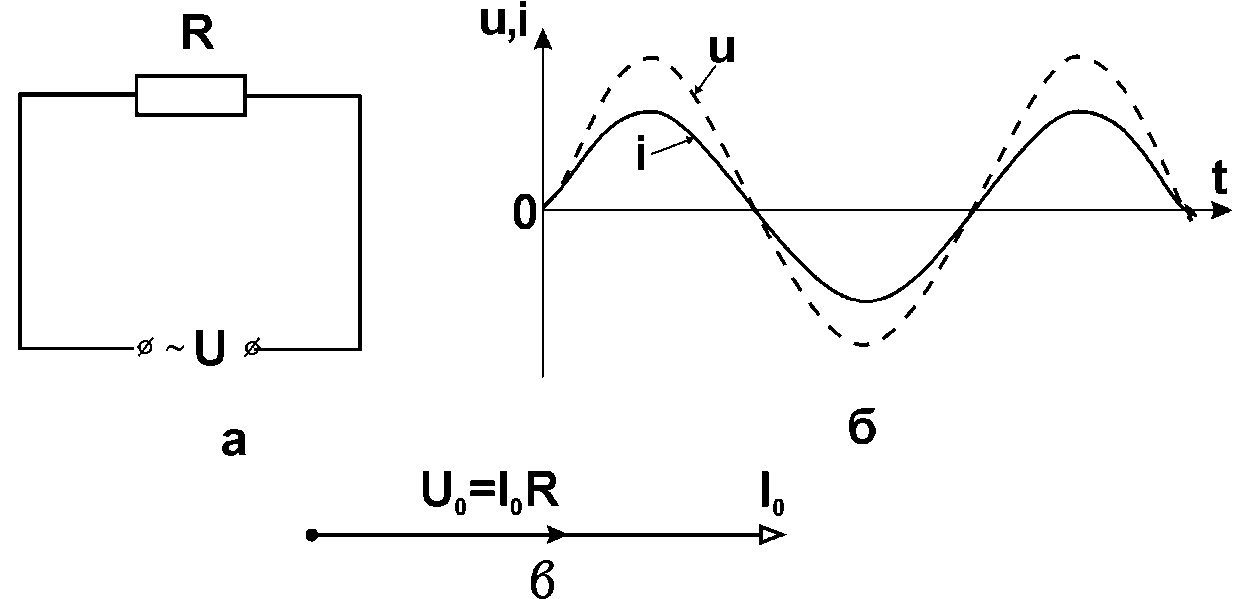
Рис.1 (а, б) Коло з активним опором Рис.1 (в) Векторна діаграма
Векторна діаграма такого кола, зображена на рис.2, де вектор струму збігається за напрямом із вектором напруги, при цьому зсув за фазою дорівнює нулю. Ці дві електричні величини мають лише дійсне значення.
Закон Ома для такого кола через амплітудні значення, діючі значення та в комплексній формі має вигляд:
; 
; 
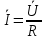
Також необхідно враховувати збільшення опору провідників змінного струму, що пов’язано з явищем витиснення струму на поверхню провідника. Поверхневий ефект враховується введенням коефіцієнта
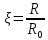
де
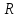– опір провідника до постійного струму;
– опір цього ж провідника до змінного струму.Індуктивність у колі змінного струму
Раніше вже говорили про котушки індуктивності, про параметри індуктивності
, що характеризує здатність елемента електричного кола створювати магнітне поле при протіканні по ньому електричного струму. Умовне позначення індуктивності – L. У колі змінного струму, такий елемент як котушка індуктивності створює навколо себе магнітне поле, яке індукує у витках елемента ЕРС самоіндукції 
. Ця ЕРС є реакцією елемента на появу змінного магнітного поля, тому її можна назвати реактивною.Якщо у колі з індуктивним елементом протікає синусоїдний струм
, то ЕРС самоіндукції 
.За Другим законом Кірхгофа
, звідси напругу можна записати співвідношенням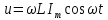 
, або 
,де
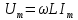.З цієї формули витікає ряд важливих обставин:
По-перше, зсув фаз
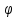між напругою на індуктивності та струмом через індуктивність буде мати вигляд 
. Таким чином, при вмиканні індуктивності на синусоїдну напругу струм у колі залишається синусоїдним і відстає від напруги на чверть періоду (2 в).Коли струм проходить через нуль, напруга на індуктивності досягає максимального(додатного або від’ємного) значення, тому що швидкість зміни струму при його проходженні через нуль є максимальною.
По-друге, величина
має розмірність опору і називається індуктивним опором при частоті струму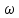 
. Індуктивний опір відрізняється від активного і має назву реактивного опору 
. Комплексний індуктивний опір визначається співвідношенням 
.
Рис. 2
Отже напруга
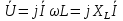на ідеальному індуктивному елементі випереджає вектор струму по фазі на кут 
, або на 
. А символ 
показує, що вектор струму треба повернути на чверть періоду проти ходу годинникової стрілки.Величини, обернена опорові
, називається провідністю і позначається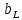 
, 
. І нарешті, миттєві значення потужності що поступає до індуктивності можна визначити:
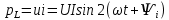. Вона має амплітуду 
і коливається з подвійною частотою (2 б).Енергія магнітного поля, що накопичується в індуктивності, визначається:
Вона змінюється в часі з подвійною частотою в межах від 0 до
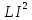, досягаючи максимального значення при амплітудному значенні струму та зменшуючись до нуля 
. При потужності 
, енергія забирається від джерела та запасається у магнітному полі котушки, а при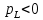 
, енергія магнітного поля повертається назад до джерела. Так відбувається коливання між джерелом та індуктивністюЗакон Ома для кола з індуктивним елементом через амплітудні, діючі та в комплексній формі має вигляд
; 
; 
.Ємність у колі синусоїдного струму
Ємність або ємнісний елемент накопичує енергію в електричному колі. Умовне позначення елемента можна відтворити у вигляді мал. (3 а). Властивості ємнісного елемента обумовлені можливістю накопичення на ньому електричного заряду, пропорційного напрузі на елементі
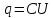. Де 
– заряд (Кл); С – коефіцієнт пропорційності (Ф).Якщо напруга, що прикладається до конденсатора (рис.4), незмінна, то заряди на його обкладинках відповідно
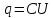та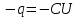 
також будуть незмінними і струм через конденсатор проходити не буде 
. Якщо коло містить ємнісний елемент, то струм змінюється за законом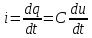 
.
Рис. 3 Конденсатор у колі змінного струму
Відповідно, якщо напруга змінюється за синусоїдним законом, то
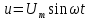,при цьому за синусоїдним законом буде змінюватися і заряд конденсатора
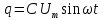,і через конденсатор буде проходити струм
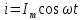
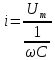
При вмиканні ємності на синусоїдну напругу у колі встановлюється синусоїдний струм, що випереджає струм на чверть періоду.
Величина
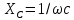має розмірність опору та називається ємнісним опором. Ємнісний опір, як і індуктивний, є реактивним опором. Індуктивний опір підвищується з підвищенням частоти струму та індуктивності елемента. Ємнісний опір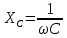 
при постійному струмі дорівнює нескінченності і зменшується при підвищенні частоти змінного струму та ємності елемента.Векторна діаграма кола з ємністю мал. (3 в) складена як, помноження вектора струму, що відповідає повороту цього вектора на
за ходом годинникової стрілки.Закон Ома для кола синусоїдного струму, що містить лише ємнісний опір, має вигляд:
; 
; 
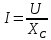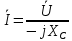.Енергія електричного поля ємності визначається:
