7. Криві другого порядку: коло, еліпс.
Колом називається множина всіх точок площини, рівновіддалених від даної точки цієї площини, яка називається центром.
Рівняння кола з центром у початку координат і радіусом R має вигляд:
.Рівняння кола з центом у точці
і радіусом R має вигляд:
.Рівняння кола у загальному вигляді записують так:
,де
- сталі коефіцієнти.Еліпсом називається множина точок площини, сума відстаней яких до двох даних точок, що називаються фокусами, є величина стала, більша за відстань між фокусами.
Рівняння еліпса, фокуси якого лежать на осі Ох, має вигляд:
,д
Рис. 7.1
е а – довжина великої півосі; b – довжина малої півосі (ріс 7.1).
Залежність між параметрами a,b,c виражається співвідношенням:
.Ексцентриситетом еліпса називається відношення фокусної відстані 2сдо великої осі 2а:
.Якщо центр симетрії еліпса знаходиться у точці
, а осі симетрії паралельні осям
, то рівняння еліпса має вигляд:
.Зразки розв’язування задач.
Задача 1. Складіть рівняння кола з центром у точці М(2;-3) і з радіусом, що дорівнює 2. Побудуйте це коло.
Розв’язання
. За умовою задачі маємо: а=2, b=-3, R=2. Підставивши ці значення в рівняння кола, дістанемо:
або
.Б
Рис. 7.2
удуємо центр кола, тобто точку М(2,-3). З центра М радіусом, який дорівнює 2, опишемо коло ( рис.7.2).
Задача 2. Складіть рівняння кола, яке має центр в точці (5;-7) і проходить через точку (2;-3).
Розв’язання.
Знайдемо радіус кола як відстань від центра до його точки:
.В рівняння кола підставимо координати центра і знайдену величину радіуса:
.Задача 3. Знайдіть координати точок перетину кола
з осями координат.Розв’язання.
Коло перетинається з віссю абсцис у точках, ординати яких дорівнюють нулю. Припустивши, що рівнянні кола y=0, дістанемо:
;
, 
.Отже, коло перетинається з віссю абсцис у точках (-2; 0) і (8;0).
Коло перетинається з віссю ординат у точках, абсциси яких дорівнюють нулю. Припустивши, що в рівнянні кола х=0, дістанемо:
;
; 
.Отже, коло перетинається з віссю ординат у точках
і (0;6).Задача 4. Складіть рівняння кола, яке проходить через точки
, 
, 
.Розв’язання
. Нехай точка
- центр шуканого кола, тоді 
, як радіуси того самого кола. Маємо:
,
,
.Складемо систему рівнянь відносно невідомих а і b та розв’яжемо її:
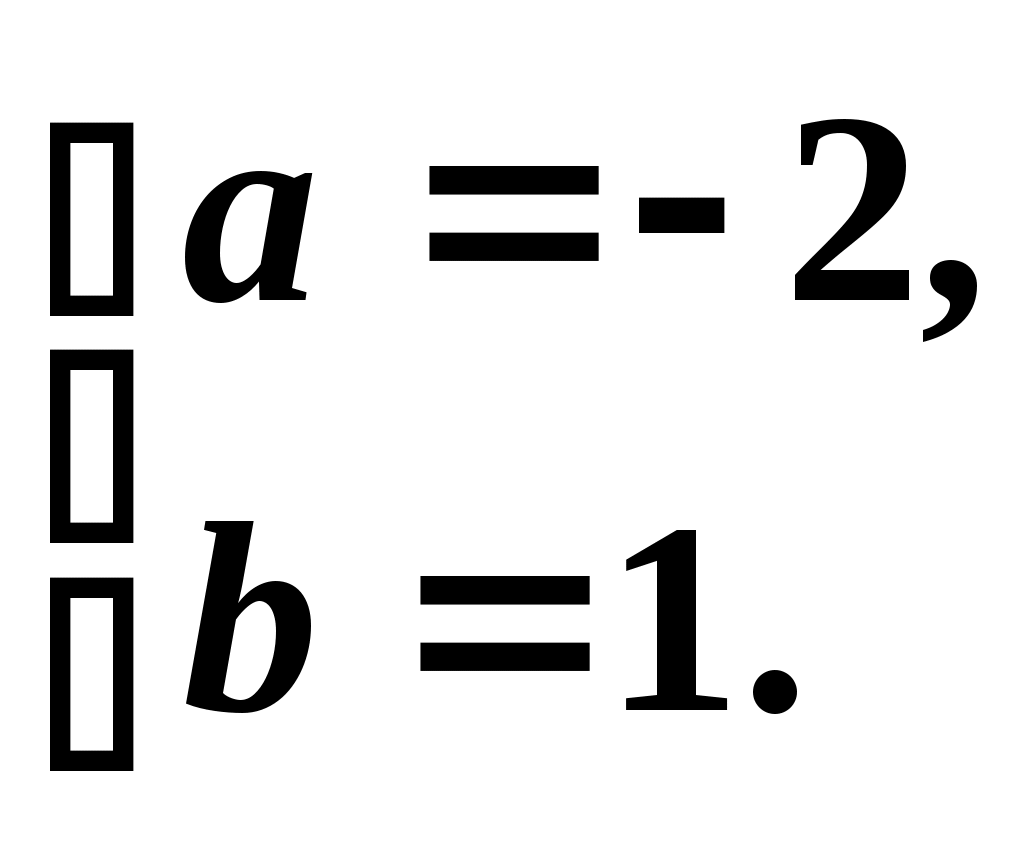
.Знаходимо
.Отже, шукане рівняння кола має вигляд:
.Задача 5. Знайдіть координати центра і радіус кола
.Розв’язання.
Перепишемо це рівняння у вигляді:
.Доповнивши двочлени
і 
до повних квадратів, дістанемо:
або
.Звідки
, 
, 
, тобто центр кола – точка (4;5), а радіус дорівнює 7.Задача 6. Скласти рівняння еліпса з фокусами на осі Ох, якщо велика ось дорівнює 12, а відстань між фокусами дорівнює 8.
Р
Рис. 7.3
озв’язання.
З умови впливає, що
і с=4. Знаходимо . Підставивши значення
і 
в рівняння еліпса, дістанемо 
.Задача 7. Дано еліпс
. Знайти координати фокусів еліпса і відстань між ними.Розв’язання.
З рівняння еліпса маємо
і 
. Тоді 
. Отже координати фокусів 
і 
, а відстань між ними 
.Задача 8. Скласти рівняння еліпса з фокусами на осі Ох, якщо його велика вісь дорівнює 14, а ексцентриситет
.Розв’язання.
З умови маємо:
, 
. Підставивши в це співвідношення значення а, дістанемо 
.Далі знаходимо
. Отже, шукане рівняння має вигляд:
або 
.Задача 9. Скласти рішення еліпса з фокусами на осі Ох, якщо він проходить через точки
і 
.Розв’язання.
Щоб скласти рівняння еліпса, треба знайти параметри
і 
. Підставивши в рівняння еліпса координати даних точок, дістанемо систему рівнянь:
; 
; 
;
; 
; 
; 
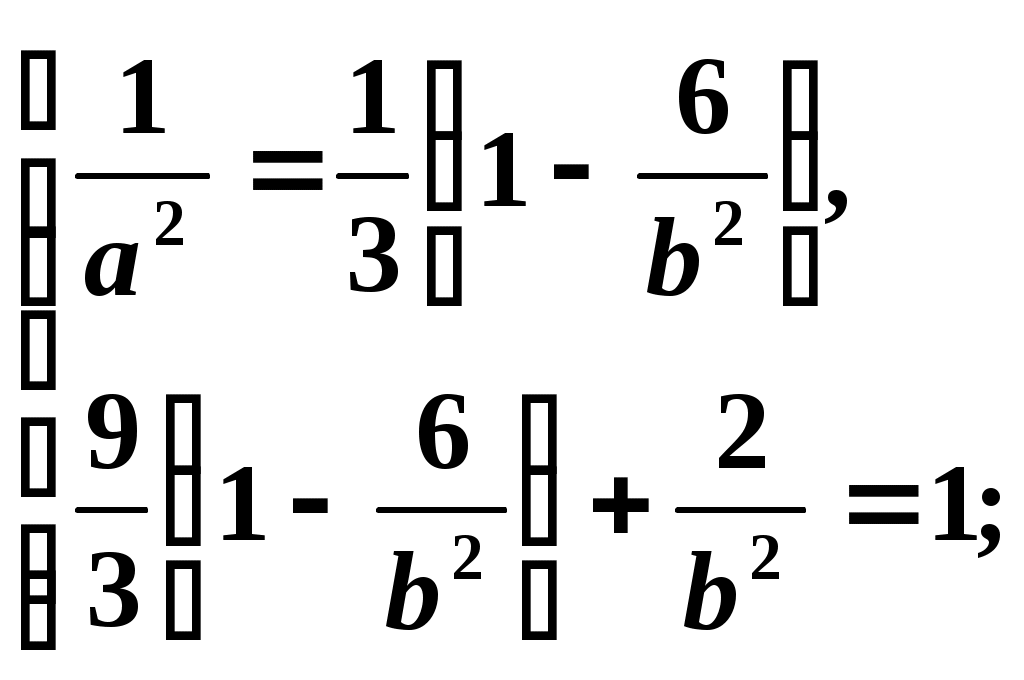
.Отже, шукане рівняння має вигляд:
.Завдання для самостійної роботи.
Задача 1. Складіть рівняння еліпса з фокусами на осі Ох, якщо відстань між фокусами дорівнює 12, ексцентриситет
.Задача 2. Скласти рівняння еліпса з фокусами на осі Ох, якщо він проходить через точки А (6;4) і В (8;3).
Задача 3. Знайдіть відстань між центрами кіл
і 
.Задача 4. Знайдіть кут між прямими, які проходять через центр кола
і через фокуси еліпса .Задача 5. Складіть рівняння кола, яке проходить через точки А(-8;3) і В(2;-7), якщо центр його лежить на прямий
.Задача 6. Записати рівняння лінії, зображеної на рисунку.
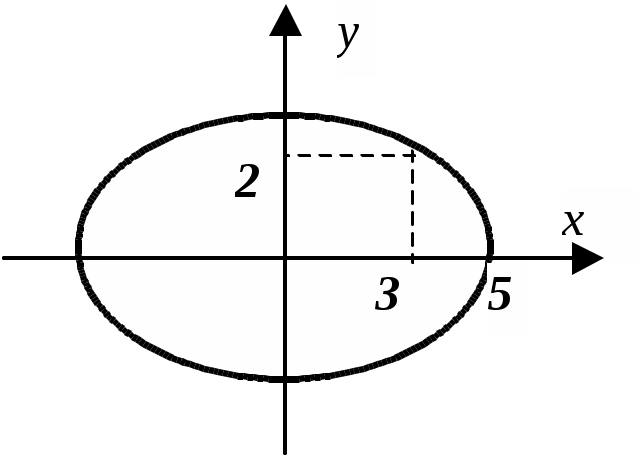
Задача 7. Записати рівняння лінії, зображеної на рисунку.
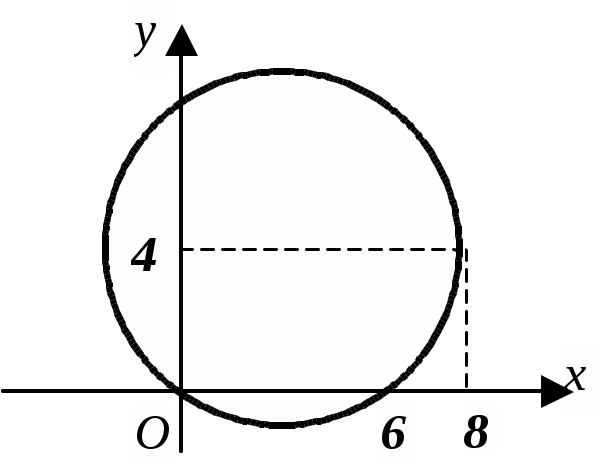
Задача 8. Побудувати криву, задану рівнянням
, та знайти її ексцентриситет.8. Криві другого порядку: гіпербола, парабола.
Гіпербола
Гіперболою називається множина точок площини, абсолютна величина різниці відстаней яких до двох даних точок, що називається фокусами, є величина стала (2а), менша за відстань між фокусами (2с).
Рівняння гіперболи, фокуси якої лежать на осі на осі Ох, має вигляд:
, (8.1)де а – довжина дійсної півосі; b
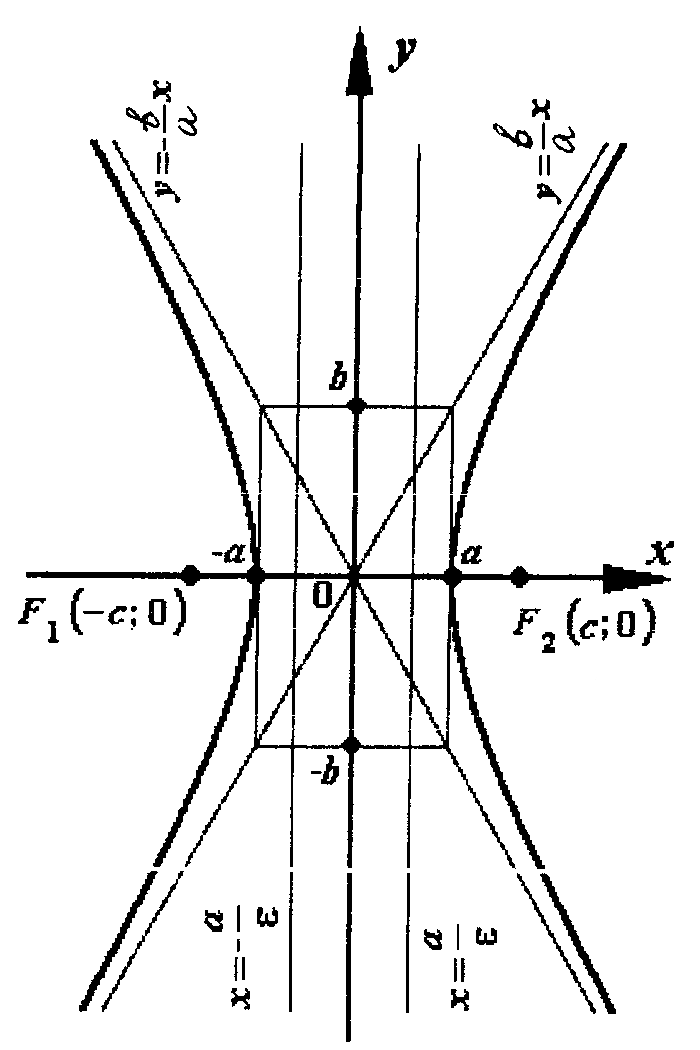
Рис. 8.1
– довжина уявної півосі (рис. 8.1).
Залежність між параметрами а, b, с виражається співвідношенням:
.Ексцентриситетом гіперболи називається відношення півфокусної відстані до її дійсної півосі:
.Фокуси гіперболи знаходяться у точках
, 
.Гіпербола має дві асимптоти, рівняння яких
, а також дві директриси, рівняння яких 
. Якщо дійсна та уявна півосі рівні (а=b), то гіпербола називається рівносторонньою. Рівняння рівносторонньої гіперболи має вигляд:
,а рівняння її асимптот
.Якщо фокуси гіперболи лежать на осі Оy у точках
, 
, то її рівняння має вигляд:
. (8.2)Р
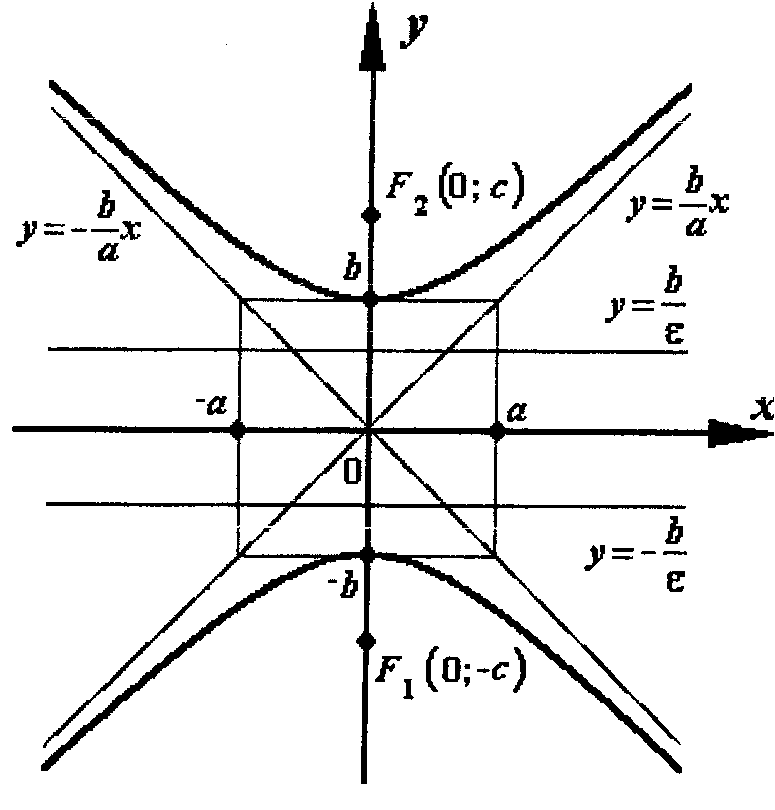
Рис. 8.2
івняння асимптот такої гіперболи
, а рівняння директрис 
(рис. 8.2).Гіперболи (8.1) і (8.2) називається спряженими.
Рівняння рівносторонньої гіперболи з фокусами на осі Оy має вигляд:
.Якщо центр симетрії гіперболи знаходиться у точці
, а осі симетрії паралельні осям Ох, Оy, то рівняння гіперболи має вигляд:
; (8.1*')
. (8.2*)1 2 3 4