28 Спектральное представление стационарных процессов. Прямое и обратное преобразование Фурье.
Для удобства говорим о центрированных случайных процессах.
Периодический процесс (периодическая корреляционная функция).
, 
,где
Так как корреляционная функция - четная функция, то есть
, для центрированного процесса 
- действительная, то мы можем перейти к косинус преобразованиям Фурье:
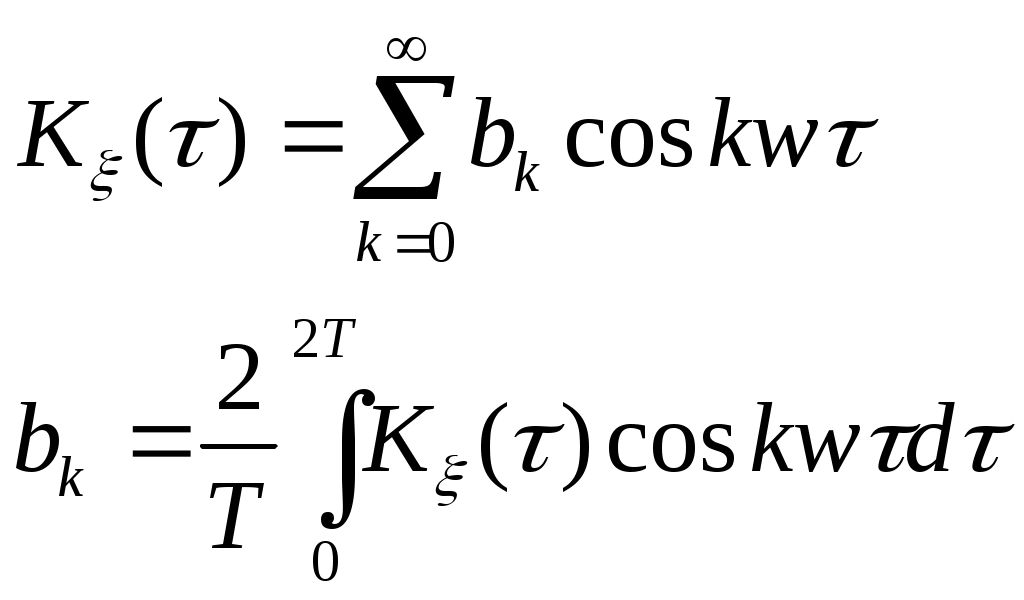
Дисперсия стационарного периодического процесса:
Дисперсия стационарного случайного процесса, представленная спектральным разложением, равна сумме всех дисперсий гармоник его спектрального разложения.
Непериодический процесс:
,
-интервал между соседними частотами.
W(w) -спектральная плотность стационарного случайного процесса, плотность распределения дисперсий по непрерывным частотам.
Она же - спектр мощности, спектральная плотность мощности, энергетический спектр. W(w) характеризует удельную меру мощности.
Опять вернемся к общему преобразованию Фурье.
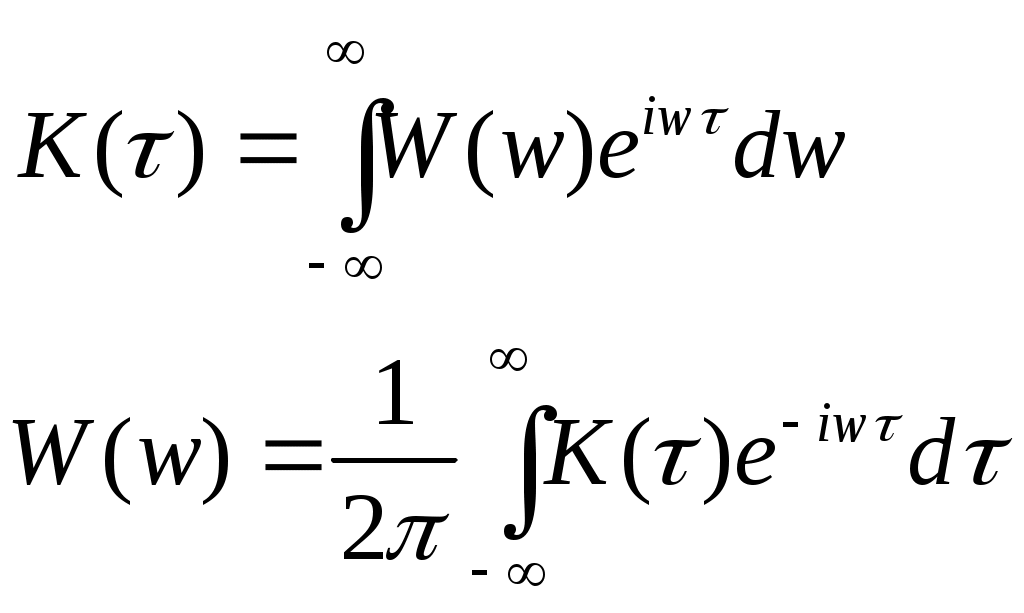- формулы Винера-ХинчинаПрямое преобразование Фурье имеет вид:
Это преобразование существует, если существует
Тогда обратное преобразование Фурье будет иметь вид:
, где S(w) - спектр сигнала.Преобразование Фурье
обладает следующими основными свойствами:линейность
;если сигнал
- действительный, то 
-является четной, а 
-нечетной функцией;для смещенного во времени сигнала
;при изменении масштаба времени
.29. Свойства спектров сигналов. Особенности спектра действительного сигнала.
Свойства спектров сигналов
линейность
;если сигнал
- действительный, то -является четной, а -нечетной функцией;для смещенного во времени сигнала
;при изменении масштаба времени
.Спектр сигнала s(t) содержит компоненты и на отрицательной полуоси частот, причем
( для действительных сигналов они совпадают ).Спектр плотности действительного случайного процесса
:
Найти:
.
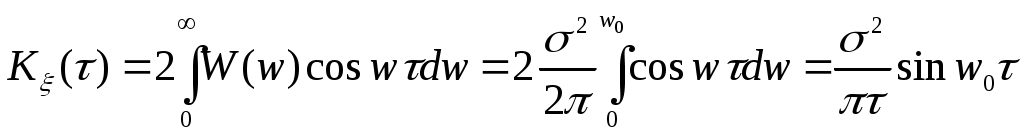
В точках
, то есть сечения ,
- некоррелируемы.2. Существует ли стационарный случайный процесс, имеющий корреляционную функцию вида:
? 
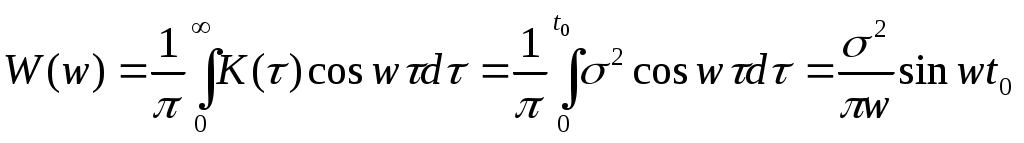
Эта корреляционная функция не может быть корреляционной функцией стационарного процесса, так как спектральная плотность должна быть больше 0, а в данном случае есть синус, который приводит к минусу.
30 Понятие спектральной плотности. Свойства спектральной плотности. Спектральная плотность действительного процесса.
Спектральной плотностью (спектром мощности) стационарного случайного процесса
называют функцию 
, которая связана с корреляционной функцией 
взаимно обратными преобразованиями Фурье:
, 
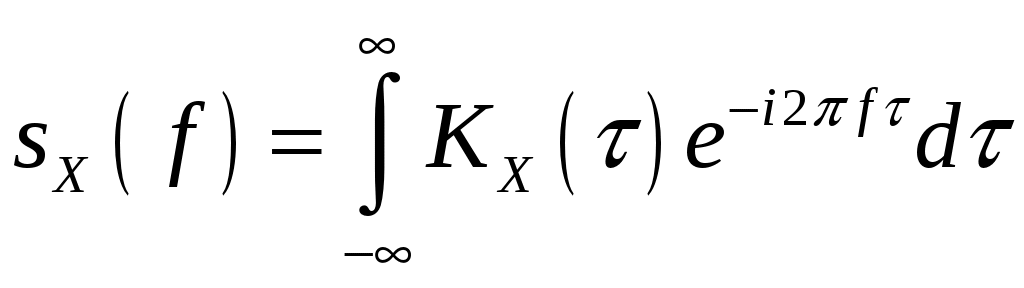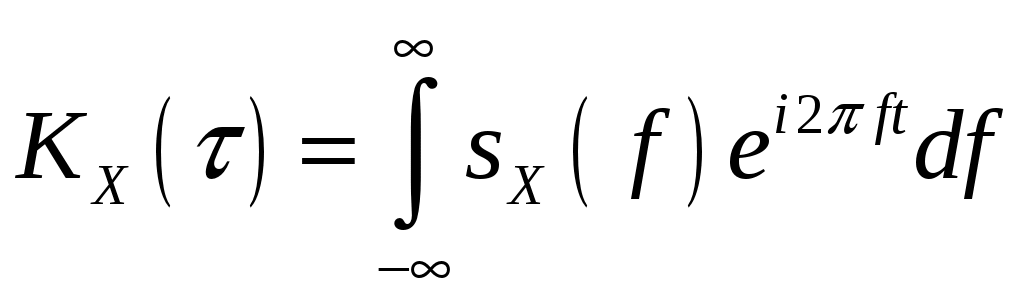.Свойства спектральной плотности.
1. Если
- вещественный, то 
- четная функция.2. Спектральная плотность - неотрицательная функция, то есть:
.3. Если дисперсия
ограничена, то W(w) - интегрируемая функция:
34 Связь спектральной плотности и корреляционной функции. Спектральная плотность периодического процесса.
Функция корреляции и спектр плотности связаны между собой преобразованиями Фурье.Еще раз о физическом смысле W(w).
- распределение энергии по частоте.
- средняя мощность флуктуации процесса.
- односторонний спектр мощности.35 Спектр дискретного сигнала. Смысл теоремы Котельникова.
Спектр же дискретного сигнала, представляет собой периодическую по частоте последовательность копий спектров
исходного сигнала, сдвинутых относительно друг друга на величину 
(или 
), что составляет период последовательности. Очевидно, периодическим по частоте с тем же периодом является и модуль спектра 
и его аргумент, т.е. фазовый спектр.Отметим, что
(или 
) – это частота дискретизации. Таким образом, период спектральной функции дискретного сигнала равен частоте дискретизации.
36 Дискретное преобразование Фурье. Частота дискретизации и частота Найквиста.
При численном моделировании (обработке) процессов непрерывный во времени сигнал заменяется дискретным рядом. Когда реализация
представлена временным рядом с интервалом дискретизации 
, длина реализации 
связана с объёмом выборки 
равенством 
. Предполагается, что рассматриваемая реализация имеет периодический характер и период её равен . Непрерывная реализация заменяется временным рядом 
, где 
, а непрерывное преобразование Фурье 
– дискретной последовательностью 
, 
. Соответствующая пара преобразований Фурье определяется формулами
, ,
, 
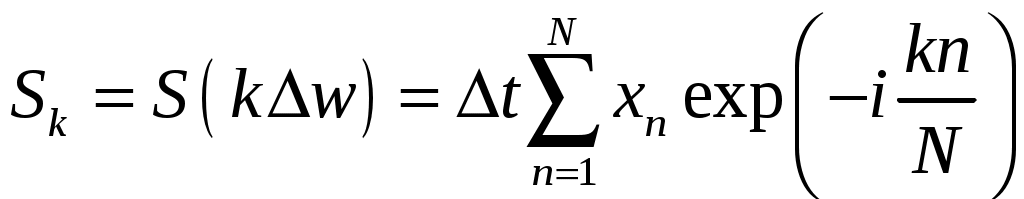.Свойства ДПФ
1. ДПФ — линейно, т.е. сумме сигналов соответствует сумма их спектров.
2.
и 
— периодические функции по модулю 
3.
— постоянная составляющая
.4. Для действительных процессов, т.к.
спектр симметричен
.
Частота дискретизации (или частота сэмплирования) показывает, какое количество раз АЦП произведёт замер той или иной характеристики аналогового сигнала. Измеряется в Герцах, хотя обычно применяют килогерцы.
Формирование дискретного сигнала из аналогового называется дискретизацией сигнала.
Чем выше частота дискретизации, тем более качественной будет оцифровка. Как следует из теоремы Котельникова для того чтобы одназначно восстановить исходный сигнал, частота дискретизации должна превышать наибольшую необходимую частоту сигнала в два раза.
Используемые частоты дискретизации звука:
8 000 Гц — телефон, достаточно для речи;
11 025 Гц;
22 050 Гц — радио;
44 100 Гц — аудио компакт-диск;
48 000 Гц — DVD, DAT
Частота Найквиста — в цифровой обработке сигналов частота, равная половине частоты дискретизации. Названа в честь Гарри Найквиста.
Из теоремы Котельникова следует, что при дискретизации сигнала полезную информацию будут нести только частоты ниже частоты Найквиста. Частоты выше частоты Найквиста являются зеркальным отображением нижних частот. Если спектр сигнала не имеет составляющих выше частоты Найквиста, то он может быть оцифрован и затем восстановлен без искажений.
К примеру, в аудио компакт-дисках используется частота дискретизации 44100 герц. Частота Найквиста для них — 22050 герц, она ограничивает верхнюю полосу частот, до которой звук может быть воспроизведён без искажений.
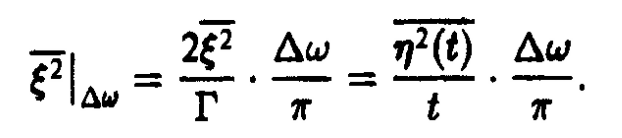
37 Какими способами можно определить спектр и спектральную плотность по временной реализации.
Функции спектральной плотности можно вводить в рассмотрение тремя различными способами: c помощью ковариационных функций, через преобразование Фурье и с помощью фильтрации.
1. Определение спектров через ковариационные функции
Этот способ определения спектральной плотности составляет операция взятия преобразования Фурье от предварительно вычисленной ковариационной функции. Пусть известны ковариационные функции
и случайных процессов и , соответственно, а также их взаимные ковариационные функции 
и . Преобразования Фурье функций в соответствии с (1.33) определяются формулами:  | | | |
 | | | |
 | | | |
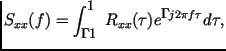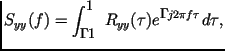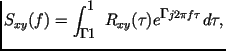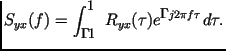 | | | (П56) |
Функции и называются двусторонними спектральными плотностями случайных процессов и , соответственно, т. к. они определены как для положительных, так и для отрицательных частот. Функции и называются двусторонними взаимными спектральными плотностями случайных процессов и .
Обратные преобразования Фурье имеют вид:
 | | | |
 | | | |
 | | | |
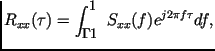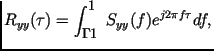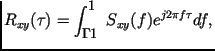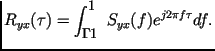 | | | (П57) |
В отличие от спектральной плотности , взаимные спектральные плотности не обязательно должны быть вещественными положительными и четными функциями частоты . Они обладают следующими свойствами.
1.
; здесь знак "*" указывает на комплексно-сопряженную величину. Это свойство показывает, что вместо вычисления двух функций и достаточно вычислить лишь одну из них, а вторую можно определить через вычисленную.2. Вещественные части
и 
являются четными функциями частоты .3. Мнимые части
и 
являются нечетными функциями частоты .4. Для всех частот выполняется неравенство
что позволяет перейти к нормированной взаимной функции -- функции когерентности, которая меняется в пределах от до (см. ниже).
2. Определение спектров через финитное преобразование Фурье
Преобразование Фурье (1.33) дает разные результаты для каждой из реализаций СП, поэтому его можно использовать только как частотное представление отдельной реализации, но не всего случайного процесса. Это означает, что для получения статистической характеристики СП к процедуре преобразования Фурье отдельной реализации необходимо каким-то образом добавить процедуру усреднения по ансамблю. Кроме того, для стационарных случайных процессов преобразование Фурье (1.33) не существует, поскольку не выполняется условие абсолютной интегрируемости (1.35). Это условие не удовлетворяется для любой не равной нулю реализации СП. На практике невыполнение этого условия означает, что полученная характеристика является несостоятельной: разброс (дисперсия) функции сравним со средним значением функции, т.е. ошибка оценки велика.
Для того, чтобы преобразование существовало для каждой реализации, необходимо их видоизменить. Рассмотрим новый случайный процесс , реализации которого ограничены на временном интервале
:
Для усеченного процесса будет существовать преобразование Фурье , поскольку выполняется условие интегрируемости в среднеквадратическом:
 | (П61) |
которое является более строгим, чем условие абсолютной интегрируемости (1.35). Далее необходимо перейти к пределу для того, чтобы построенные в пределе функции являлись оценками исходного случайного процесса.
Оказывается, что такой предельный переход возможен, если вместо функции рассматривать другую функцию:
Если выражение (1.62) разделить на , то его левая часть будет характеризовать среднюю энергию процесса на временном интервале от до .
разделим обе части соотношения (1.62) на , усредним выражение (1.62) по ансамблю путем вычисления математического ожидания и, переходя к пределу при , получим соотношение:
 | (П63) |
Левая часть выражения (1.63) записана с учетом формулы (1.17), в которой .
Для стационарного СП математическое ожидание среднего квадрата реализации равно самому среднему квадрату
, т.е. средней энергии СП. спектр мощности является усредненным по времени математическим ожиданием от квадрата преобразования Фурье усеченной реализации.
Взаимные спектральные плотности двух случайных процессов и выражаются через преобразование Фурье усеченных реализаций следующим образом:
 | | | |
 | | | |
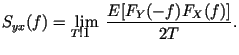3. Определение спектров с помощью фильтрации
Поскольку спектральная плотность характеризует распределение средней энергии по частотам, ее можно определить через процедуру узкополосной фильтрации и усреднение энергии отфильтрованного сигнала. Обычно такая процедура включает следующие операции:
-- получение реализации длительности ;
-- выбор полосно-пропускающего линейного фильтра с центральной частотой и полосой пропускания . Чем уже полоса используемого фильтра, тем выше частотное разрешение спектра мощности;
-- частотную фильтрацию реализации с помощью полосно-пропускающего фильтра с граничными частотами
и . В результате этой операции получается отфильтрованная реализация 
;-- возведение в квадрат мгновенного значения отфильтрованной реализации. В результате получается реализация
;-- усреднение реализации
по ее длительности . В результате получается оценка средней энергии отфильтрованной реализации;-- деление величины средней энергии на ширину полосы пропускания фильтра , в результате чего получается оценка плотности средней энергии в частотном диапазоне от
до , т.е. оценка спектра мощности на частоте :
Далее описанная процедура повторяется для других значений центральных частот фильтра
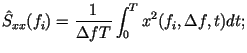:  | | | (П65) |
Для вычисления взаимной спектральной плотности нужно обобщить описанную процедуру на случай двух сигналов:
| | |  | |
 | |  | |
 | |  | |
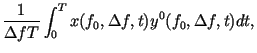где
-- сдвинутый по фазе на отфильтрованный сигнал 
.38 Процесс авторегрессии 1 порядка, его свойства. Алгоритм моделирования.
Случайный процесс
называется процессом авторегрессии 1 порядка или кратко AR(1), если для него выполняется соотношение :
(1)где
- некоторая константа, 
- дискретное время, 
- независимые от значения случайной величины 
.Авторегрессия 1-го порядка - марковский процесс с дискретным временем. Характеризуется тем, что задание его состояния в некоторый момент времени определяет дальнейшее вероятностное поведение процесса безотносительно ко всему прошлому множеству состояний. Чем ближе
к 1, тем более гладко ведут себя траектории. Если 
, то временная реализация будет прыгать. При 
- случайное броуновское движение (
зависит от времени).Мы будем рассматривать только стационарные процессы авторегрессии. Это условие накладывает определенные ограничения на параметр
.Определим числовые характеристики стационарного процесса авторегрессии.
Условия стационарности:
,
.Взяв мат. ожидание от обеих частей (1)
,получим
если 
.Взяв дисперсию от обеих частей (1), получим
. Отсюда следует (учитывая, что 
), что 
, 
.Таким образом, для стационарного процесса AR(1) получаем, что
и для любых 
.Найдем значения корреляционной функции
:
;…
.Из этих соотношений следует, что нормированная корреляционная функция
.39 Обобщенный телеграфный сигнал. Как его промоделировать.
Обобщенный телеграфный сигнал -
случайный процесс
, который может принимать только два значения: 1 и -1. Моменты времени изменения значения процесса образуют простейший пуассоновский поток событий с интенсивностью 
(среднее число смен значений за единицу времени). Теоретические значения характеристик процесса:
, 
,корреляционная функция
,нормированная корреляционная функция
.
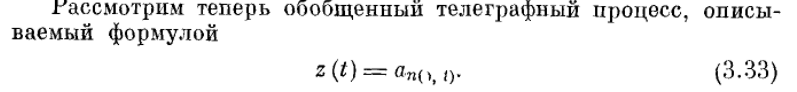
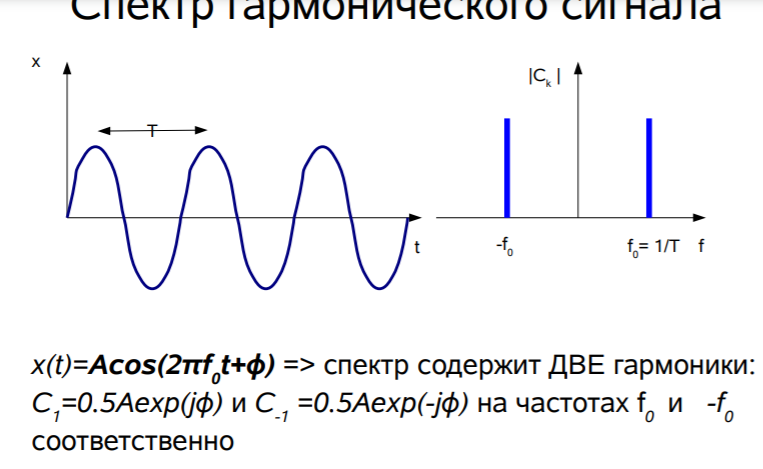
40 Гармонический сигнал со случайной фазой. Его корреляционная функция, спектр. Как его промоделировать.
Гармонический сигнал со случайной фазой -
случайный процесс вида
, где
-случайная величина, имеющая равномерное распределение на отрезке 
, 
и 
- константы, определяющие амплитуду и частоту. Теоретические значения характеристик процесса: , 
, корреляционная функция
, нормированная корреляционная функция
.
41 Простейший поток событий. Его свойства. Как его промоделировать.
Поток событий, обладающий свойствами стационарности, ординарности и отсутствия последействияназывается простейшим (пуассоновским) потоком.
