1. Загальні означення 4 Розфарбовування графа 6

Ім'я файлу: Розфарбування графа двома кольорами.docx
Розширення: docx
Розмір: 118кб.
Дата: 15.12.2020
скачати
Пов'язані файли:
6_Методичне забезпечення індивідуальної роботи студентів (КПІЗ)
САМОСТІЙНА РОБОТА ВПХ.docx
ПМ-І-1_Слюсар_Л_О_лаб2.docx
Практика Голець.pdf
Білорусь.pptx

Зміст

Вступ 3

1. Загальні означення 4

2. Розфарбовування графа 6

1.2 Теоретична частина 6

2.2. Приклади 7

3. Розфарбовування графа двома кольорами 9

3.1. Теорема 1. 9

3.3. Алгоритм розфарбовування графа в два кольори. 10

4. Перевірка графа на двочастковість. 11

4.1. Алгоритм перевірки графа на двочастковість з використанням обхіду в глибину. 11

4.2. Алгоритм перевірки графа на двочастковість з використанням обхіду в ширину. 11

4.3. Реализація 11

Список літератури 13

Вступ

Поняття «граф» пов'язане з поняттям «графічний», «графіка». Дійсно, графові моделі мають просту і зрозумілу графічну інтерпретацію, що дозволяє з їх допомогою образно уявити найрізноманітніші об'єкти, в той же час залишаючись в рамках строгих математичних моделей.
Першою роботою з теорії графів як математичної дисципліни вважають статтю Ейлера (1736 г.), в якій розглядалася задача про Кенігсбергські мости. Ейлер показав, що не можна обійти сім міських мостів і повернутися у вихідну точку, пройшовши по кожному мосту рівно один раз. Наступний імпульс теорія графів одержала через майже 100 років з розвитком досліджень з електричних мереж, кристалографії, органічної хімії та інших наук.
З графами, самі того не помічаючи, люди часто стикаються в житті. Наприклад, графом є схема ліній метрополітену. Точками на ній представлені станції, а лініями - шляхи руху поїздів. Досліджуючи свій родовід і зводячи її до далекого предка, ми будуємо так зване генеалогічне древо. І це древо - граф.
Методи теорії графів широко застосовуються в дискретній математиці. Без них неможливо обійтися при аналізі і синтезі різних дискретних перетворювачів: функціональних блоків комп'ютерів, комплексів програм і т.д.
В даний час теорія графів охоплює великий матеріал і активно розвивається.

1. Загальні означення

Графом, в загальному випадку, називаються дві множини, що знаходяться між собою в деякому відношенні: G = (V, Е), де V - множина вершин, Е - множина зв'язків між ними. Вершини графа зображуються крапками, а зв'язки між ними - лініями довільної конфігурації.
Зв'язок невпорядкованої пари вершин називається ребром, впорядкованої - дугою. Граф, у якого всі вершини з'єднані дугами називається орієнтованим. Граф, у якого всі вершини з'єднані ребрами називається неорієнтованим, якщо в графі присутні і ребра і дуги, то такий граф називається змішаним.
Дві вершини називаються суміжними, якщо вони визначають дугу (ребро), і дві дуги називаються суміжними, якщо вони мають загальну вершину. Вершина инцидентна дузі (ребру), якщо вона є початком або кінцем цієї дуги (ребра). Аналогічно, дуга (ребро) инцидентна вершині, якщо вона входить або виходить з цієї вершини. Число дуг (ребер), інцидентних деякої вершини, називають локальною ступенем даної вершини.
Граф, в якому будь-яка пара вершин з'єднана ребром називається повним. Повний граф зазвичай позначають через К_n (n - число вершин в графі).
Число ребер повного графа m = n * (n-1) / 2. Повний підграф G` = (X`, U`) графа G = (Х, U), X`εX називається максимальним повним підграфом (МПП) або клікою, якщо цей підграф не міститься в більшому (по числу вершин) повному підграфі.
Максимальний повний підграф, що містить найбільшу кількість вершин з усіх МПП графа називається найбільшим повним підграфом (НПП). Число вершин найбільшого повного підграфа називається щільністю графа - φ (G). Якщо дві будь-які вершини підмножини X` графа G (Х, U), де X`εX не суміжні, то підмножина X` називається внутрішньо стійкою.
Підмножина ψ_i X X графа G (Х, U) називається максимальною внутрішньо стійкою підмножиною (МВСП), або незалежною підмножиною (НП), якщо додавання до неї будь-якої вершини x_jεХ робить її не внутрішньо стійкою. Підмножина Y_i буде визначатися як х_jεψ_i (Гх_j uψ_i =)
МВСП розрізняються за кількістю елементів, що входять в неї. МВСП, що містить найбільшу кількість елементів (вершин), називають найбільшою (граничною). Потужність НВСП (число вершин найбільшої ВСП) називається числом внутрішньої стійкості.
h (G) = |mах ψ_i |, где ψ_iεψ, ψ - сімейство всіх МВУП.
Число внутрішньої стійкості називає також нещільністю графа.
Завдання визначення найбільших повних подграфов і НВСП є додатковими друг до друга. Найбільшому повному підграфу графа G = (Х, U) відповідає найбільше ВСП у графі G = (Х, U), де U_повнU, U_повн- безліч ребер повного графа, побудованого на n вершинах. Аналогічні міркування можуть бути зроблені і для максимальних НП і МВСП.
Всі ці завдання відносяться до так званих NP повних завдань, тимчасова складність яких експоненційна щодо входу (числа вершин або ребер графа).
Відповідно до класифікації всіх задач теорії графів за їх складністю, завдання визначення МВСП і МПП (знаходження клік) графа за складністю належать до четвертого класу задач, для яких не існує і не може існувати точного поліномінального алгоритму, так як завдання цього класу обов'язково експоненціальні щодо входу. Завдання визначення НПП і МВСП (найбільшої кліки) відносяться до третього класу, для якого відкриття поліномінального алгоритму можливо.

2. Розфарбовування графа

1.2 Теоретична частина

Розфарбовуванням вершин графа називається призначення кольорів його вершинам. Зазвичай кольори - це числа 1,2, ..., k.
Тоді розфарбування є функцією, визначеною на множині вершин графа і приймаючої значення в множині {1,2, ... k}.
Розмальовку можна також розглядати як розбиття множини вершин:

= , где

- множина вершин кольору i.
Множини

називають кольоровими класами.
Розфарбування називається правильним, якщо кожен кольоровий клас є незалежною множиною. Інакше кажучи, в правильному розфарбовуванні будь-які дві суміжні вершини повинні мати різні кольори.
Завдання про розфарбовування полягає в знаходженні правильної розмальовки даного графа G в найменше число кольорів. Це число називається хроматичним числом графа і позначається

(G).
Правильна розфарбування графа G може виглядати наступним чином:

Рисунок 1 - Приклад розмальовки графа

Функцією Гранді називається функція на вершинах графа, що відображає вершини в безліч {1,2, ... a}, причому якщо вершина xi забарвлена в колір з номером k, то функція Гранді h(xi) = k.
Ясно, що для даного графа хроматичне число є єдиним, але функцій Гранді може бути дуже багато. Зрозуміло, що знайти хоча б одну функцію Гранді - це значить знайти одну з можливих "найкращих" розмальовок (таких розмальовок може бути багато).
Зауважимо, що якщо даний граф є повним, тобто будь-які дві вершини є суміжними, то хроматичної число такого графа одно p, де p - число вершин.

2.2. Приклади

Як приклад візьмемо граф, представлений на рисунку 2.
Кольори позначимо:

червоний: 1,

зелений: 2,

синій: 3.

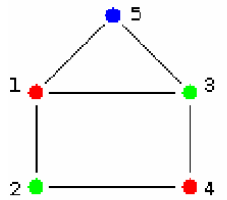
Рисунок 2 - Приклад графа

Неявний перебір
1. Розфарбовуємо вершини по порядку в мінімально можливі кольори: 1-червоний, 2 - зелений, 3 - зелений, 4 - червоний, 5 - синій.
2. Вершина номер 5 має максимальний колір (з номером 3). Спробуємо його позбутися: робимо крок повернення з вершини 5.
3. Суміжна вершина з максимальним номером, яка менше 5 - це 3. Перефарбувати її в колір більший неї (2) і менший, ніж максимальний (3) - не можна. Робимо крок повернення з вершини 3.
4. Суміжна вершина з максимальним номером, які менше 3 - це 1. Ми досягли першу вершину і завершуємо алгоритм.
Евристичний метод
1. Сортуємо вершини за ступенем: 1, 3, 2, 4, 5.
2. Офарблюємо в перший колір (червоний). Ми можемо пофарбувати вершини 1. Вершини 2 і 3 забарвити не можна, оскільки вони суміжні з 1. Вершина 4 неінцидентна, так що може бути пофарбована в червоний. Суміжну з першої вершину 5 забарвити не можна.
3. Сортуємо вершини за кількістю суміжних нефарбованих вершин: 3, 2, 5.
4. Вибираємо наступний колір - зелений. Ми можемо пофарбувати в нього вершини 2 і 3.
5. Сортуємо вершини за кількістю суміжних нефарбованих вершин: залишається тільки 5.
6. Вибираємо наступний колір - синій (3).
7. Офарблюємо останню вершину 5 в синій колір.

3. Розфарбовування графа двома кольорами

3.1. Теорема 1.

Граф можна розфарбувати в два кольори тоді і тільки тоді, коли він двочастковий.
Доведення: Якщо безліч вершин двочасткового графа можна розділити на дві незалежні підмножини так, що жодна з вершин ні в одному з цих підмножин не є суміжною до вершини з цієї ж підмножини, тоді граф G = (W, E) можна розфарбувати в два кольори.

χ (G) = 2.
Якщо ж граф можна розфарбувати в два кольори, то множину його вершин можна розділити на два непересічних множини так, щоб в кожної з них не знайшлося двох суміжних вершин. Тоді граф буде двочастковим.
3.2. Теорема Кьоніга.
Граф G = (V, E) є двоколірним тоді і тільки тоді, коли в ньому немає циклів непарної довжини.
Доведення. Якщо в графі G = (V, E) є цикл непарної довжини, то вершини цього циклу в два кольори не розфарбувати.
Доказ (продовження). Нехай в графі G = (V, E) немає циклів непарної довжини. Будемо вважати, що G - зв'язний граф, інакше можна провести аналогічні міркування для

кожної його компоненти зв'язності. Побудуємо в графі G його кістяк D. У будь-якому дереві для кожної пари вершин v, w існує рівно один шлях з v в w.

Нехай v ∈ V - якась вершина. Пофарбуємо вершини в дереві D в два кольори за таким правилом:

1) вершину w ∈ V фарбуємо в колір 1, якщо довжина шляху з v в w

парна;

2) вершину w ∈ V фарбуємо в колір 2, якщо довжина шляху з v в w

непарна.

Доказ (продовження). Доведемо, що при такій розфарбуванні в графі G = (V, E) не ребер, обидва кінці яких пофарбовані в один і той же колір. Припустимо гидке: нехай (u, w) ∈ E таке ребро, і вершини u, w пофарбовані в колір 1.

Розглянемо замкнутий маршрут в графі G: з u в v в дереві D, потім з v в w в дереві D і по ребру (u, w) в u. Довжина цього маршруту непарна, тому що довжини шляхів з u в v і з v в w в дереві D мають однакову парність. Значить, з нього можна виділити цикл непарної довжини. Протиріччя.

3.3. Алгоритм розфарбовування графа в два кольори.

Нехай заданий зв'язний граф G = (V, E).

1. Будуємо кістяк D для графа G.

2. Починаючи з довільної вершини v ∈ V пошуком в ширину розбиваємо все вершини на дві незалежних множини V1 і V2 по парності / непарності шляху з v.

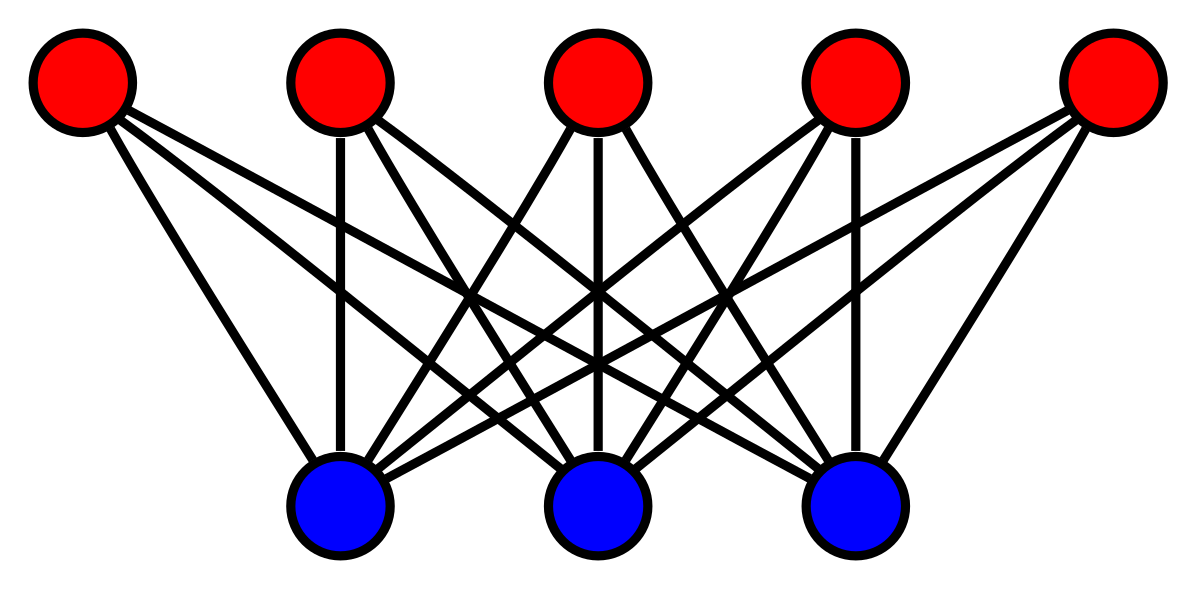
Рисунок 2 - Зображення розфарбованого двочастковго графа.

4. Перевірка графа на двочастковість.

4.1. Алгоритм перевірки графа на двочастковість з використанням обхіду в глибину.

Так як граф є двочастковим тоді і тільки тоді, коли всі цикли парні, визначити двочасткові можна за один прохід в глибину. На кожному кроці обходу в глибину помічаємо вершину. Припустимо, ми пішли в першу вершину - помічаємо її як 1. Потім переглядаємо всі суміжні вершини, і якщо не позначена вершина, то на ній ставимо позначку 2 і рекурсивно переходимо в неї. Якщо ж вона позначена і на ній стоїть та ж позначка, що і у тій, з якої йшли (в нашому випадку 1), значить граф НЕ двочастковий.

4.2. Алгоритм перевірки графа на двочастковість з використанням обхіду в ширину.

Зробимо серію пошуків в ширину. Тобто будемо запускати пошук в ширину з кожної з невідвіданих вершини. Ту вершину, з якої ми починаємо йти, ми поміщаємо в першу долю. У процесі пошуку в ширину, якщо ми йдемо в якусь нову вершину, то ми поміщаємо її в долю, відмінну від долі поточної вершину. Якщо ж ми намагаємося пройти по ребру в вершину, яка вже переглянута, то ми перевіряємо, щоб ця вершина і поточна вершина знаходилися в різних долях. В іншому випадку граф двочастковим не є. Після закінчення роботи алгоритму ми або виявимо, що граф не двочастковий, або знайдемо розбиття вершин графа на дві частки.

4.3. Реализація

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

#include

using namespace std;

vector<int> graph[100000];

char color[100000]; // Колірбудемопредставлятитипом char

// 0 - вершина ще не пофарбована; 1, 2 - різні кольори.

inline char invert(int c) {

return c == 1 ? 2 : 1;

}

void dfs(int v, char c) { //c - колірпоточноївершини

color[v] = c;

for (int u: graph[v]) {

if (color[u] == 0) { // невідвідана вершина

dfs(u, invert(c));

} else if (color[u] == c) {

cout << "Graph is not bipartite." << endl;

exit(0);

}

}

}

int main() {

// Введення графа ...

// дводольні граф може бути незв'язним (тоді існують кілька

способів фарбування).

for (int i = 0; i < n; i++) {

if (color[i] == 0) {

dfs(i, 1);

}

}

cout << "Graph is bipartite." << endl;

}

Список літератури

1. Харари Т. Теорія графів.- М., 1973.

2. Лекції по теорії графів / Емелічев В.А., Мельников О.І., Сарванов В.І., Тишкевич Р.І.- М., 1990.

3. Зиков А.А. Основи теорії графов.- М., 1987.

4. Оре О. Теорія графов.- М., 1980.

5. Свамі М., Тхуласіраман К. Графи, мережі, алгорітми.- М., 1984.

6. Вілсон Р. Введення в теорію графов.- М., 1977

7. Крістофідес Н. Теорія графів. Алгоритмічний підхід.- М., 1978

8. Рейнгольд Е., Нівергельт Ю., Део Н. Комбінаторні алгоритми.-М., 1980

скачати