1.Предмет теорії ймовірності.Класифікація подійПредмет теорії ймовірностей– вивчення ймовірнісних закономірностей масових однорідних випадкових подій.Математична наука, яка вивчає загальні закономірності випадкових явищ, незалежно від їх конкретної природи і дає методи кількісної оцінки впливу випадкових факторів на різні явища,називається теорієюймовірностей.Класифікаціяподій:Подія А називається достовірною, якщо вона обов’язково відбудеться при заданих умовах і неможливою, якщо вона при цих умовах відбутися не може.Подія А, яка може відбутися або не відбутися в одному випробуванні, називається випадковою.Події А1, А2, А3, ..., Аn називаються рівноможливими, якщо при виконанні комплексу умов, кожна з них має однакову можливість відбутися.Події А1, А2, А3, ..., Аn називаються сумісними, якщо поява однієї із них не виключає можливості появи інших, або відбуваються одночасно.Приклад № 1: 1) А – поява трьох очок при підкиданні грального кубика; В – поява непарної кількості очок при підкиданні грального кубика; 2) постріл по мішені із 3-х гармат – влучення кожної з них не виключає можливість влучення іншої. Вони можуть влучити всі три одночасно при одному пострілі.Події А і В називаються несумісними, якщо вони не можуть відбутися разом (одночасно) в одному випробуванні. (П-д: підкидання монети – якщо випав герб, то решка вже в одному випробуванні з’явитися не може).Якщо в одному випробуванні обов’язково відбудеться одна із несумісних подій A1,..., An, то ці події утворюють повну групу подій. Дві події, які утворюють повну групу, називаються протилежними. Подію, протилежну до події А, позначають A (чит. „не А”).
2.Класичне означення ймовірності.Відносна частота………………………..Відношення числа m елементарних подій, які сприяють події А, до загальної кількості n подій простору називається ймовірністю випадкової події А і позначається Р(А), тобто
.де m – число подій, які сприяють події А, n – число подій простору елементарних подій (0≤m≤n). Імовірність вірогідної події дорівнює 1, імовірність неможливої події дорівнює 0, а ймовірність Р(А) випадкової події А задовольняє умову 0<Р(А)<1.Відносною частотою події називають відношення числа випробувань, у яких подія з’явилася, до загального числа фактично зроблених випробувань. Таким чином, відносна частота події А визначається формулою
де m - число появ події, n - загальне число випробувань.Зіставляючи визначення ймовірності і відносної частоти, робимо наступний висновок: визначення ймовірності не вимагає, щоб випробування проводилися в дійсності; визначення ж відносної частоти передбачає, що випробування були проведені фактично.Іншими словами, ймовірність обчислюють до випробування, а відносну частоту - після випробування.Приклад 1. Відділ технічного контролю знайшов 3 нестандартні деталі в партії з 80 випадково відібраних деталей. Відносна частота появи нестандартних деталей
3. Статистичне означення ймовірності.Практично неможливі подіїНехай n – кількість усіх випробувань в окремій серії випробувань, а m – кількість тих випробувань, у яких відбулася подія А.Статистичною ймовірністю події А називається границя, до якої наближається відносна частота
події А при необмеженому збільшенні числа всіх випробувань, тобто
. Неможли́вою поді́єю в теорії ймовірності називається подія V{\displaystyle V}, яка в результаті досліду статися не може.Очевидно, що ймовірність неможливої події дорівнює нулю.Проте, не всяка подія, ймовірність якої дорівнює нулю, є неможливою подією. Приклад: подія, що полягає в тому, що нормально розподілена випадкова величина набуде деякого конкретного значення. Для будь-якої неперервної випадкової величини вірне твердження: ймовірність того, що випадкова величина набуде визначеного, наперед заданого значення, дорівнює нулю P={E=x0}=0.{\displaystyle P\{\xi =x_{0}\}=0} Інший приклад події з нульовою ймовірністю: експеримент полягає в тому, що монета підкидається нескінченне число разів. Подія «Монета нескінченне число разів впаде цифрою вгору» має нульову ймовірність, але вона може статися, тому також не є неможливою.Якщо обумовлена деяка допустима похибка (наприклад,{\displaystyle 10^{-50}}10 10 в -50), ту подію, ймовірність якої не перевищує значення цієї похибки, називають практично неможливою. Подія, протилежна неможливій, називається достовірною подією4.Теорема додавання ймовірності несумисних подій……Теорема 1. Ймовірність появи однієї з двох несумісних подій, байдуже якої, дорівнює сумі ймовірностей цих подій:
Дійсно, нехай - загальне число всіх можливих елементарних результатів випробувань,
– число результатів, що сприяють появі події А,
– число результатів, що сприяють появі події В. Тоді число результатів, що сприяють появі або А, або В, дорівнює
.Отже, 
, і теорема доведена. Наслідок. Ймовірність появи однієї з декількох попарно несумісних подій, байдуже, якої, дорівнює сумі ймовірностей цих подій: 
Дійсно, взявши для простоти 
та позначивши
, маємо: 
Теорема 2. Сума ймовірностей подій 
, які утворюють повну групу несумісних подій, дорівнює одиниці: 
Дійсно,подія є достовірною. Тому
. Оскільки події несумісні, то , що і доводить теорему 2.Нагадуємо, що протилежним називаються дві єдино можливі події, які утворюють повну групу несумісних подій: 
та
.Із теореми 2 випливає, що сума ймовірностей протилежних подій дорівнює одиниці: 
Прийнято позначати 
,
; отже,
.5.Теорема додавання ймовірностей сумісних подій……Розглянемо питання про ймовірність суми сумісних подій.Нагадаємо, що дві події називаються сумісними, якщо поява однієї з них не виключає появи іншої події в одному і тому ж випробуванні.Має місце така теорема про ймовірність суми сумісних подій.Теорема. Ймовірність появи хоча б однієї з двох сумісних подій дорівнює сумі ймовірностей цих подій без ймовірності їх сумісної появи.Дійсно, подію
можна представити як суму трьох несумісних подій:
.Отже, згідно з наслідком з теореми 1, маємо:
.Зауважимо, що події А та В можна представити, як суми двох несумісних подій: 
,
.Тому 
,
.Звідси знаходимо:
Такимчином, 
, і, остаточно,
, що і потрібно було довести.Зауважимо, що у випадку несумісних подій 
, і ми одержуємо теорему додавання ймовірностей несумісних подій (теорему 1). Відзначимо також, що події А та В можуть бути як незалежними, так і залежними.Ми підійшли до питання про те, як знаходити 
– ймовірність добутку двох подій.6.Теорема множення ймовірностей незалежних подій………Означення: подія А називається незалежною від події В, якщо ймовірність події А не залежить від того, відбулась чи ні подія В.Теорема: Ймовірність добутку двох незалежних подій А і В дорівнює добутку ймовірностей цих подій, тобто Р(АВ) = Р(А) Р(В).Наслідок.Твердження справджується і для подій. Тобто, якщо події Аі , де , попарно незалежні та здійснення довільної кількості із них не змінює ймовірності здійснення інших, то .
7.Умовна ймовірності.Теорема множення ймовірностей залежних подій……..Умовна ймовірність.Означення ймовірності події ґрунтується на припущенні про існування деякого незмінного комплексу умов S. Якщо жодних інших обмежень, крім умов S, під час обчислення ймовірності Р(А) не накладається, то таку ймовірність називають безумовною. Однак часто доводиться розглядати ймовірності випадкових подій із додатковою умовою, що відбулася деяка подія В, яка має додатну ймовірність. Такі ймовірності будемо називати умовними і позначати P(A B) або Р(А / В), або P (A) B – це означає ймовірність події А за умови, що подія В відбулася. Пояснимо спочатку на прикладі суть умовної ймовірності та пов’язані з нею питання. Теорема множення ймовірностей залежних подій.Означення. Умовною ймовірністю
називається ймовірність події В, обчислена в припущенні, що подія А вже з’явилась.Сформулюємо теорему множення ймовірностей.Теорема. Ймовірність сумісної появи двох подій дорівнює добутку ймовірності однієї з них на умовну ймовірність другої, обчислену в припущенні, що перша подія вже з’явилась: 
Оскільки 
, то
і, отже,
. 8.Формула повної ймовірності та формула БейссаНехай подія А може відбутись тільки разом з однією із попарно несумісних подій
…, , які називаються гіпотезами (hypothesis) і утворюють повну групу 
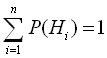. Тоді, якщо відбулась подія А, то це означає, що відбулась одна із попарно несумісних подій 
. Це означає: 
. Використавши теорему додавання, одержимо:
.З теореми множення ймовірностей
, і =1, 2, 3, …, n.
. (1.1)Одержана формула (1.1) називається формулою повної імовірності.
Після цього нас цікавить питання про те, як зміняться ймовірності гіпотез , і= 1, 2…, n, якщо подія А відбулась. Тобто, як обчислити
. Справедливі рівності: 
, звідки
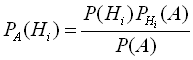(1.2)Ця формула називається формулою Байєса.
9.Повторні випробування .Формула Бернуллі…….Коли виконуються послідовні випробування, то за результатом кожного з них може відбутися або не відбутися деяка подія A.Нехай проводиться п випробувань (одноразових експериментів), причому ймовірність настання події А у кожному випробуванні Р(А) = р і не залежить від результатів інших випробувань. Такі випробування називаються незалежними. Оскільки ймовірність настання події А в одному випробуванні дорівнює p, то ймовірність її ненастання Р(Ặ) = 1 - р = q.Знайдемо ймовірність того, що при п випробуваннях подія А настане рівно k разів (0<k<п). Виконавши п послідовних випробувань, матимемо різні комбінації результатів. Ті комбінації результатів, в яких подія відбудеться к разів, називатимемо сприятливими.Визначимо ймовірність Р однієї сприятливої комбінації. Сприятливою комбінацією є добуток п незалежних у сукупності подій: k появ події Ặ і п - k появ події Ặ. Отже, за теоремою про ймовірність добутку подій, незалежних у сукупності, дістанемо, що ймовірність однієї сприятливої комбінації дорівнює
Здійснення складної події, яка полягає в тому, що подія А настає рівно k разів, рівносильна появі принаймні однієї сприятливої комбінації. Іншими словами, така складна подія є сумою всіх сприятливих комбінацій. Проте сприятливі комбінації попарно несумісні. Тому за теоремою про додавання ймовірностей попарно несумісних подій дістанемо ймовірність появи події А k разів при п випробуваннях: 
де N - кількість усіх можливих комбінацій.Залишається визначити N. Розглянемо спочатку приклад.Нехай п = 3, k = 2. Сприятливими тут є такі комбінації результатів випробувань, коли з трьох випробувань подія А відбувається двічі. Позначатимемо появу події А знаком "+", а появу події Ặ знаком "-". Тоді сприятливі комбінації можна зобразити у вигляді рядків такої таблиці:| 1 | 2 | 3 |
| - | - | - |
| + | + | - |
| + | - | + |
| - | + | + |
1 2 3 4 5 6 7