Ім'я файлу: 4 Метод дихотомии алгоритм и блок-схема.docx
Розширення: docx
Розмір: 24кб.
Дата: 16.12.2022
скачати
Пов'язані файли:
339-737-1-SM.pdf
Розширення: docx
Розмір: 24кб.
Дата: 16.12.2022
скачати
Пов'язані файли:
339-737-1-SM.pdf
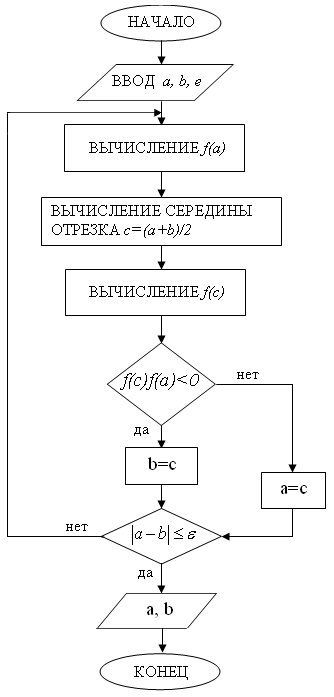
\\ Обобщенный алгоритм выглядит так:
задать начальный интервал [Xleft..Xright];
убедиться, что на концах функция имеет разный знак;
повторять
выбрать внутри интервала точку X;
сравнить знак функции в точке X со знаком функции в одном из концов;
если совпадает, то переместить этот конец интервала в точку X,
иначе переместить в точку X другой конец интервала;
пока не будет достигнута нужная точность.
В этом алгоритме есть пара мест, нуждающихся в уточнении:
"Нужная точность" определяется условиями задачи. Иногда требуется, чтобы значение функции было меньше некой наперед заданной величины, но это редко; чаще всего требуется определить значение корня с отклонением от истинного в заданных пределах. Лучше всего, если можно с уверенностью гарантировать интервал, в котором находится корень.
Метод выбора точки деления - ключевой для скорости работы метода. Хорошо, если функция, чей корень мы ищем, проста и быстро вычисляется; но внутри функции могут быть и матричные операции, и численное интегрирование, и все что угодно; так что главным критерием оптимизаци является минимизация числа делений (естественно, без ухудшения точности метода).