
Ім'я файлу: КУРСОВА РОБОТА.docx
Розширення: docx
Розмір: 73кб.
Дата: 30.05.2021
скачати
Пов'язані файли:
Оператори проектування.doc
Розширення: docx
Розмір: 73кб.
Дата: 30.05.2021
скачати
Пов'язані файли:
Оператори проектування.doc
Відношення ортогональності для характерів
Спочатку, введемо позначення. Нехай
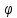 і
і 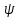 – дві функції з групи
– дві функції з групи 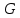 на поле комплексних чисел. Покладемо:
на поле комплексних чисел. Покладемо: 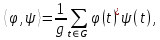 | (30) |
де
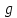 – порядок групи
– порядок групи 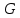 . Визначений таким чином добуток
. Визначений таким чином добуток 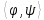 задовольняє всім аксіомам скалярного добутку: він полілінійний по
задовольняє всім аксіомам скалярного добутку: він полілінійний по 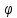 , та лінійний по
, та лінійний по 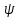 , та
, та 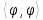 > 0 для кожної функції
> 0 для кожної функції 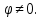 Такий добуток називається скалярним добутком функції, визначених на групі.
Такий добуток називається скалярним добутком функції, визначених на групі.Теорема 3. (1) Нехай
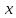 – характер деякого незвідного зображення. Тоді
– характер деякого незвідного зображення. Тоді 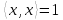 (інакше кажучи
(інакше кажучи 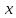 має “довжину 1”).
має “довжину 1”).(2) Нехай
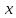 і
і 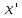 – характери неізоморфних незвідних зображень, тоді
– характери неізоморфних незвідних зображень, тоді 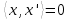 (інакше кажучи
(інакше кажучи 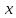 та
та 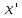 ортогональні).
ортогональні).Д о в е д е н н я. Нехай
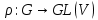 – незвідне зображення з характером
– незвідне зображення з характером 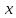 , і нехай
, і нехай 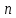 – його степінь, тоді
– його степінь, тоді 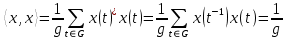 | (31) |
(за твердженням 1). Якщо ж зображення
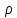 задано в матричній формі
задано в матричній формі 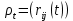 , то
, то 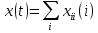 , звідки
, звідки 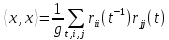 | (32) |
Використовуючи наслідок 3 тверження 3, бачимо, що
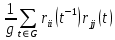 дорівнює 0 при
дорівнює 0 при 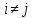 і дорівнює
і дорівнює 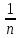 при
при 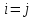 . Але так як індекс
. Але так як індекс 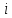 приймає
приймає 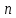 значень, то ми отримуємо звідси, що
значень, то ми отримуємо звідси, що 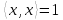 .
.Друге твердження теореми доводиться аналогічно з використанням наслідку 2 замість наслідку 3.
Теорема 4. Нехай
 –- лінійне зображення групи
–- лінійне зображення групи 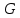 з характером
з характером 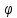 ; припустимо, що
; припустимо, що  розкладається в пряму суму незвідних зображень,
розкладається в пряму суму незвідних зображень, 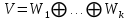 . . | (33) |
Тоді, якщо
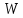 – деяке незвідне зображення з характером
– деяке незвідне зображення з характером 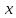 , то число
, то число 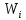 ізоморфних зображенню
ізоморфних зображенню 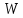 , дорівнює скалярному добутку
, дорівнює скалярному добутку 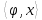 .
.Д о в е д е н н я. Нехай
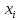 – характер зображення
– характер зображення 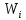 . Тоді на основі твердження 2 ми маємо:
. Тоді на основі твердження 2 ми маємо: 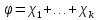 . . | (34) |
Звідки
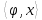 =
= 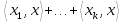 . Але за попередньою теоремою
. Але за попередньою теоремою 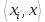 дорівнює 1 або 0 в залежності від того, чи ізоморфне зображення
дорівнює 1 або 0 в залежності від того, чи ізоморфне зображення 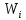 зображенню
зображенню 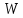 , чи ні. Що і доводить теорему.
, чи ні. Що і доводить теорему.Наслідок 1. Число зображень
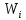 , ізоморфних даному зображенню
, ізоморфних даному зображенню 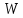 , не залежить від вибору розкладу.
, не залежить від вибору розкладу.(Це число називається кратністю входження
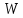 в зображення
в зображення  .)
.)Д о в е д е н н я. Дійсно, скалярний добуток
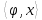 не залежить від вибраного розкладу.
не залежить від вибраного розкладу.З а у в а ж е н н н я. В цьому сенсі можна говорити про “едність” розкладу даного зображення на незвідні.
Наслідок 2. Два зображення, що мають один і той же характер – ізоморфні.
Д о в е д е н н я. Згідно з наслідком 1, очевидно, що це справді так, адже вони містять однакову кількість разів будь яке задане незвідне зображення.
Згідно з попередніми результатами вивчення зображень ототожнюється з вивченням їх характерів. Нехай
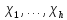 – усі різні характери незвідних зображень групи
– усі різні характери незвідних зображень групи 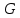 і
і 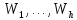 - відповідні незвідні зображення, тоді кожне зображення
- відповідні незвідні зображення, тоді кожне зображення  ізоморфно прямій сумі вигляду:
ізоморфно прямій сумі вигляду: 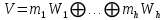 , , | (33) |
де
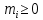 – цілі числа. В такому випадку характер
– цілі числа. В такому випадку характер 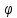 зображення
зображення  дорівнює сумі
дорівнює сумі  і
і 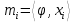 . (Зокрема такі зображення можна застосувати до тензорного добутку
. (Зокрема такі зображення можна застосувати до тензорного добутку 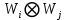 двох незвідних зображень
двох незвідних зображень 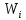 та
та  і показати що добуток
і показати що добуток 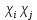 розкладається, як:
розкладається, як: 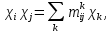 | (34) |
де всі
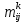 – цілі числа, та усі
– цілі числа, та усі 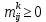 . Із відношення ортогональності між
. Із відношення ортогональності між 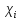 випливає, що
випливає, що 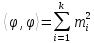 | (34) |
Звідси, також, випливає наступна теорема.
Теорема 5. Якщо
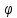 характер деякого зображення
характер деякого зображення  , то
, то 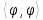 є цілим числом і
є цілим числом і 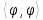 = 1 тоді і тільки тоді, коли
= 1 тоді і тільки тоді, коли  – незвідна.
– незвідна.Справді,
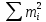 – ціле число, що дорівнює 1 тоді і тільки тоді, коли одне з
– ціле число, що дорівнює 1 тоді і тільки тоді, коли одне з 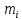 дорівнює 1, а всі інші 0, тобто
дорівнює 1, а всі інші 0, тобто  ізоморфно одному з
ізоморфно одному з 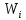 .
.Таким чином, ми отримаємо критерій незвідності зображення.
ВИСНОВОК
В даній роботі розглянуто загальні відомості про теорію зображення груп та її принципи. Розглянуто фундаментальні теореми, твердження та їх наслідки. Досліджено розвинення ідей спрощення та оптимізації цих теоретичних викладок.
А також розглянуті початки теорії характерів. Переосмислено Лему Шури та решту фундаментальних матеріалів. Вироблена нова методологія до використання характерів.
В процесі написання роботи було зроблено багато висновків, щодо теорії груп, та зображень останніх.
Список використаної літератури
Винберг Э.Б. Линейные представления групп. Наука, 1985.
Дрозд Ю.А., Кириченко В.В. Конечномерные алгебры. Вища школа, 1980.
Наймарк М.А. Теория представлений групп. М., Наука, 1976.
Ж.-П. Серр. Линейные представления конечных групп. Мир, 1970.
Холл М. Теория групп. М., изд-во иностр. л-ры, 1962. − 468 с.
1 2 3 4 5 6 7