
Ім'я файлу: КУРСОВА РОБОТА.docx
Розширення: docx
Розмір: 73кб.
Дата: 30.05.2021
скачати
Пов'язані файли:
Оператори проектування.doc
Розширення: docx
Розмір: 73кб.
Дата: 30.05.2021
скачати
Пов'язані файли:
Оператори проектування.doc
ТЕОРІЯ ХАРАКТЕРІВ
Характер зображення
Нехай
 – векторний простір з базисом
– векторний простір з базисом 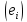 із
із 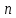 елементів і
елементів і 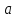 – деяке відображення простору
– деяке відображення простору  в себе з матрицею
в себе з матрицею 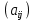 . Слідом відображення називається скаляр:
. Слідом відображення називається скаляр: 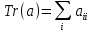 . . | (16) |
Відомо що слід дорівнює сумі власних значень відображення
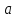 (з урахуванням їх кратностей і не залежить від вибору базису
(з урахуванням їх кратностей і не залежить від вибору базису  .
.Нехай тепер
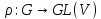 – деяке лінійне зображення скінченної групи
– деяке лінійне зображення скінченної групи 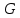 в векторному просторі
в векторному просторі  .
.Для кожного елементу
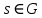 покладемо:
покладемо: 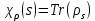 . . | (17) |
Звідки ми отримуємо, таким чином, функції
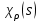 на групі
на групі 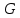 з комплексними значеннями котра називається характером зображення
з комплексними значеннями котра називається характером зображення 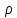 . Важливість цієї функції визначається тим, що вона характеризує зображення, що розглядається.
. Важливість цієї функції визначається тим, що вона характеризує зображення, що розглядається. Твердження 1. Нехай
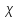 – характер деякого зображення
– характер деякого зображення 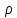 степені
степені 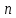 , тоді
, тоді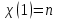 ;
;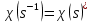 для будь-якого
для будь-якого 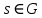 ;
;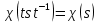 , для будь-яких
, для будь-яких 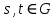 .
.Де
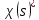 – комплексне спряжене до
– комплексне спряжене до 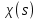 .
.Д о в е д е н н я. Так як простір
 , має розмірність
, має розмірність 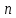 , то
, то 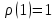 і
і 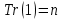 , звідки слідує твердження (1).
, звідки слідує твердження (1).Для доведення твердження (2) помітимо, що кожний елемент
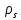 має скінченний порядок, відповідно, ця властивість є характерною і для всіх його власних значень
має скінченний порядок, відповідно, ця властивість є характерною і для всіх його власних значень 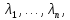 і, зрозуміло, що вони по абсолютній величенні дорівнюють 1 (це слідує зокрема і з того, що
і, зрозуміло, що вони по абсолютній величенні дорівнюють 1 (це слідує зокрема і з того, що 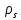 можуть бути зображенні в вигляді унітарних матриць, що було розглянуто в пункті 3 попереднього розділу). Маємо,
можуть бути зображенні в вигляді унітарних матриць, що було розглянуто в пункті 3 попереднього розділу). Маємо, 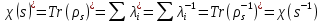 . . | (18) |
Формулу
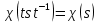 , можна переписати в вигляді
, можна переписати в вигляді 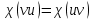 , припустивши, що
, припустивши, що 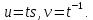 В такому вигляді вона є наслідком відомої формули:
В такому вигляді вона є наслідком відомої формули: 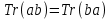 , , | (19) |
що є дійсною для довільних лінійних відображень
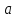 і
і 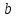 простору
простору  в себе. Доведення закінчено.
в себе. Доведення закінчено.З а у в а ж е н н н я. Функція
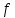 на групі, що задовольняє рівності
на групі, що задовольняє рівності 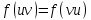 – називається центральною функцією. Пізніше ми розглянемо властивість, за якою будь-яка центральна функція є лінійною комбінацією характерів.
– називається центральною функцією. Пізніше ми розглянемо властивість, за якою будь-яка центральна функція є лінійною комбінацією характерів.Твердження 2. Нехай
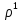 :
: 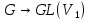 ,
, 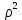 :
: 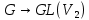 − лінійні зображення групи
− лінійні зображення групи 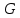 і
і 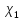 ,
, 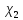 − їхні характери. Тоді
− їхні характери. ТодіХарактер
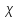 прямої суми зображень
прямої суми зображень 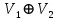 дорівнює
дорівнює 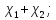
Характер
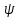 тензорного добутку зображень
тензорного добутку зображень 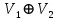 дорівнює
дорівнює 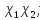
Д о в е д е н н я. Уявимо
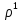 і
і 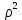 в матричній формі
в матричній формі 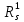 і
і 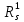 . Тоді зображення
. Тоді зображення 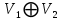 в матричній формі має вигляд:
в матричній формі має вигляд: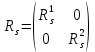
Звідки
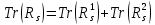 , тобто
, тобто 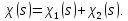
Аналогічно доводиться і твердження (2).
В позначення п. 2.5 маємо
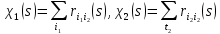 | (20) |
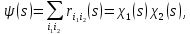 | (21) |
що і треба було довести.