
Ім'я файлу: КУРСОВА РОБОТА.docx
Розширення: docx
Розмір: 73кб.
Дата: 30.05.2021
скачати
Пов'язані файли:
Оператори проектування.doc
Розширення: docx
Розмір: 73кб.
Дата: 30.05.2021
скачати
Пов'язані файли:
Оператори проектування.doc
Підзображення
Нехай
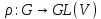 − деяке лінійне зображення
− деяке лінійне зображення  – векторний підпростір простору V. Припустимо, що підпростір
– векторний підпростір простору V. Припустимо, що підпростір  інваріантний щодо дій групи
інваріантний щодо дій групи 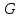 в уявленні ρ, тобто для кожного елемента
в уявленні ρ, тобто для кожного елемента 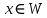 всі елементи виду
всі елементи виду  . Тоді обмежене
. Тоді обмежене 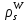 автоморфізму
автоморфізму 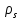 на
на  є автоморфізмом цього підпростору і, очевидно,
є автоморфізмом цього підпростору і, очевидно, 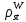 =
=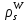 ◦
◦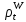 . Таким чином,
. Таким чином, 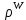 :
:  є лінійним поданням групи
є лінійним поданням групи 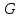 у просторі
у просторі  . Ми будемо називати його підзображенням зображення ρ.
. Ми будемо називати його підзображенням зображення ρ.Приклад. Розглянемо регулярне зображення групи
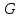 у просторі
у просторі 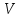 (Аналогічно до прикладу (В) з розділу 2.2), і візьмемо в якості
(Аналогічно до прикладу (В) з розділу 2.2), і візьмемо в якості  одномірний підпростір простору
одномірний підпростір простору 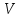 , породжене елементом
, породжене елементом 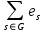 . Тоді
. Тоді 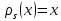 , звідки слідує, що
, звідки слідує, що  підзображення підставлення ρ, яке ізоморфно одиничному зображенню.
підзображення підставлення ρ, яке ізоморфно одиничному зображенню. Перш ніж рухатися далі, нагадаємо деякі поняття, які стосуються векторних просторів. Нехай
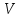 − векторний простір і
− векторний простір і  ,
, 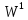 – підпростори простору
– підпростори простору 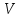 . Кажуть, що
. Кажуть, що 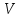 є пряма сума підпросторів
є пряма сума підпросторів  і
і 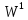 , якщо для кожного вектору
, якщо для кожного вектору 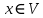 існує однозначне розкладання виду
існує однозначне розкладання виду 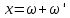 , де
, де  і
і  це рівносильно тому, що перетин W ⋂
це рівносильно тому, що перетин W ⋂ 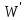 дорівнює нулю і
дорівнює нулю і 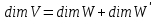 . Будемо писати тоді
. Будемо писати тоді 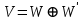 і називати підпростір
і називати підпростір 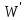 доповненням до підпростору
доповненням до підпростору  . Відображення
. Відображення 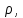 зіставляє кожному вектору
зіставляє кожному вектору 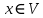 його компоненту ω із простору
його компоненту ω із простору  , називається проектором простору V на простір
, називається проектором простору V на простір  (асоційованим з прямим розкладанням
(асоційованим з прямим розкладанням  ⊕
⊕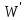 ) Образом проектору
) Образом проектору 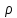 є всі підпростори
є всі підпростори  і
і  для кожного вектору
для кожного вектору 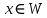 . Навпаки, якщо деяке лінійне відображення
. Навпаки, якщо деяке лінійне відображення 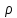 володіє цими властивостями, то простір
володіє цими властивостями, то простір 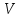 , як легко бачити, зображується у вигляді прямої суми образу
, як легко бачити, зображується у вигляді прямої суми образу  і ядра
і ядра 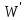 (тобто множини тих векторів
(тобто множини тих векторів 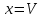 , для яких
, для яких 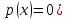 відображення
відображення 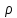 ; при цьому
; при цьому 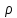 є проектором. Цим способом встановлюється взаємно однозначна відповідність між проекторами простору V на підпростір
є проектором. Цим способом встановлюється взаємно однозначна відповідність між проекторами простору V на підпростір  і доповненням
і доповненням 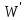
до підпростору
 .
.Повернемося знову до підзображень.
Теорема 1. Нехай
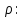
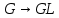 (
(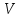 ) – лінійне зображення групи
) – лінійне зображення групи 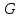 у просторі
у просторі 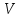 і
і  – деякий підпростір векторного простору
– деякий підпростір векторного простору 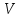 , інваріантне відносно
, інваріантне відносно 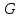 . Тоді існує доповнення
. Тоді існує доповнення 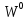 до підпростору
до підпростору  у
у 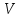 , яке також інваріантне відносно G.
, яке також інваріантне відносно G.
Д о в е д е н н я. Нехай
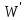 − яке-небудь доповнення до підпростору
− яке-небудь доповнення до підпростору  у
у 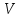 і
і 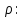
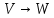 − відповідний проектор. Розглянемо усереднення
− відповідний проектор. Розглянемо усереднення  образів проектору
образів проектору 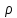 при діях елементів групи
при діях елементів групи 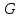 ,
,  | (9) |
(де g – порядок групи
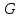 ). Оскільки
). Оскільки 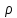 відображає
відображає 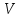 на
на  і
і  переводить підпростір W в себе, то
переводить підпростір W в себе, то  також відображає V в W. З іншої сторони, якщо
також відображає V в W. З іншої сторони, якщо 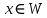 , то
, то 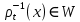 , звідки
, звідки 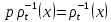 ,
,  і
і 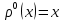 . Таким чином,
. Таким чином,  є проектором, відповідним деякому доповненню
є проектором, відповідним деякому доповненню 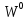 до підпростору
до підпростору  у
у 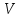 . При цьому
. При цьому 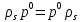 для кожного елементу
для кожного елементу 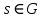 . Справді,
. Справді, 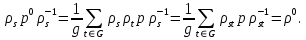 | (10) |
Якщо ж
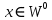 і
і 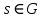 , то
, то  , звідки
, звідки 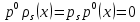 , тобто
, тобто 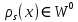 . Це означає, що підпростір
. Це означає, що підпростір 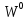 інваріантний відносно G. Теорма доведена.
інваріантний відносно G. Теорма доведена.З а у в а ж е н н я. Припустимо, що простір
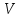 забезпечено деяким скалярним добутком
забезпечено деяким скалярним добутком 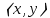 , задовольняє звичайним вимогам: лінійність по y, напівлінійність по
, задовольняє звичайним вимогам: лінійність по y, напівлінійність по 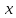 і
і 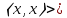 0 при
0 при 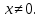 Припустимо, крім того, що цей скалярний добуток інваріантний відносно дій групи
Припустимо, крім того, що цей скалярний добуток інваріантний відносно дій групи 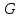 , інакше кажучи, справедлива рівність
, інакше кажучи, справедлива рівність 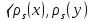 〉=
〉=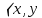 〉 для усіх
〉 для усіх 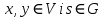 . Цьому ми завжди можемо домогтися, замінюючи у випадку необхідності
. Цьому ми завжди можемо домогтися, замінюючи у випадку необхідності 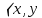
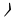 на
на 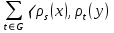
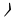 . При цих припущеннях ортогональне доповнення
. При цих припущеннях ортогональне доповнення 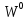 до інваріантного підпростору W в V буде, очевидно, інваріантним відносно
до інваріантного підпростору W в V буде, очевидно, інваріантним відносно 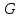 доповненням до W, ми отримуємо інше доведення теореми 1. Відмітимо, що інваріантність скалярного добутку
доповненням до W, ми отримуємо інше доведення теореми 1. Відмітимо, що інваріантність скалярного добутку 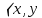
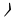 означає, що в ортонормальному базисі (
означає, що в ортонормальному базисі ( 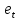 ) простору
) простору 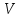 всі матриці
всі матриці 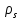 ,
, 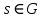 , є унітарними.
, є унітарними. Збережемо позначення та припущення теореми 1. Нехай
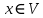 − довільний вектор і ω,
− довільний вектор і ω, 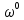 − його проекції на підпростори
− його проекції на підпростори  і
і 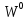 відповідно. Тоді
відповідно. Тоді  , звідки
, звідки 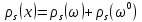 , і оскільки підпростори
, і оскільки підпростори  і
і 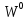 інваріантні відносно групи
інваріантні відносно групи 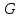 , то
, то 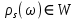 і
і 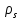 (
(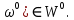 Отже,
Отже, 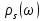 і
і 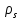 (
(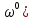 є проекціями вектора
є проекціями вектора 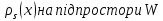
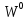 . З цього слідує, що знання зображень
. З цього слідує, що знання зображень  і
і 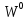 дозволяє відновити зображення
дозволяє відновити зображення 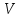 . У такому випадку говорять, що зображення V є пряма сума зображень
. У такому випадку говорять, що зображення V є пряма сума зображень  і
і 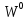 і позначають це так:
і позначають це так: 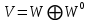 . Кожен елемент простору
. Кожен елемент простору 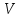 ототожнюється при цьому з парою
ототожнюється при цьому з парою 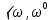 〉, де
〉, де  і
і  зображення
зображення  і
і 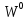 задані в матричній формі
задані в матричній формі 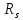 і
і 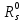 , то зображення
, то зображення 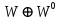 задається матрицями виду
задається матрицями виду 
Аналогічно визначається пряма сума будь-якого кінцевого сімейства зображень.