
2.4 Обертання в просторі
Задача
В дану правильну чотирикутну призму вписати правильну трикутну призму так, щоб площини їх основ збіглися і одне ребро знаходилося на прямій
 , яка лежить на бічній грані та паралельна бічному ребру призми.
, яка лежить на бічній грані та паралельна бічному ребру призми.Аналіз. Припустимо, що задача розв’язана і правильна трикутна призма
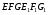 вписана в дану правильну чотирикутну призму
вписана в дану правильну чотирикутну призму  (Рис.2.9). Помічаємо, що при повороті ребра
(Рис.2.9). Помічаємо, що при повороті ребра  навколо прямої
навколо прямої  на
на 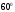 воно співпадає з ребром
воно співпадає з ребром 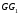 . Якщо разом з ребром повернути і площину
. Якщо разом з ребром повернути і площину 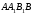 , тоді ребро
, тоді ребро 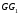 можна розглядати як лінію перетину поверненої грані з гранью
можна розглядати як лінію перетину поверненої грані з гранью 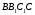 .
. Побудова
ПобудоваБудуємо правильну чотирикутну призму
 , будуємо пряму
, будуємо пряму 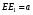 (
(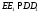 ).
).Повертаємо грань навколо прямої на та знайдемо лінію перетину її з гранью. Це буде друге ребро шуканої призми.
Повертаємо ребро
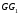 в зворотному напрямку на
в зворотному напрямку на 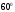 і знаходимо третє ребро
і знаходимо третє ребро  . Перше ребро призми співпадає з прямою
. Перше ребро призми співпадає з прямою  .
.Доведення. Побудована призма-шукана. Дійсно, ребра її лежать на гранях призми, при тому одне з них співпадає з прямою
 та двогранні кути дорівнюють
та двогранні кути дорівнюють 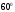 [1, c. 86].
[1, c. 86].Дослідження. Задача завжди можлива, так як бічні грані перпендикулярні між собою і після повороту на
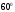 грань
грань 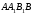 не буде паралельна грані
не буде паралельна грані 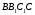 і тому перетнеться з нею. Так як можна повернути також грань
і тому перетнеться з нею. Так як можна повернути також грань 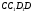 на кут
на кут 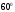 навколо прямої
навколо прямої  , тоді буде мати місце друге розв’язання.
, тоді буде мати місце друге розв’язання.2.5 Задачі на побудову перерізів многогранників
Задача
Побудувати переріз призми
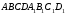 площиною, що проходить через точки
площиною, що проходить через точки 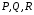 .
.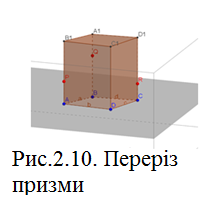 Побудуємо слід січної площини на площину нижньої основи призми. Розглянемо грань
Побудуємо слід січної площини на площину нижньої основи призми. Розглянемо грань 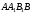 . У цій грані лежать точки перетину
. У цій грані лежать точки перетину  і
і  . Проведемо пряму
. Проведемо пряму 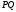 .
. Продовжимо пряму
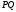 ,яка належить перерізу, до перетину з прямою
,яка належить перерізу, до перетину з прямою  Отримаємо точку
Отримаємо точку 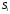 , що належить сліду.
, що належить сліду.Аналогічно отримаємо точку
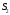 перетином прямих
перетином прямих  і
і 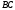 .
.Пряма
 -слід січної площини на площину нижньої основи призми.
-слід січної площини на площину нижньої основи призми.Пряма
 перетинає сторону
перетинає сторону 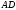 в точці
в точці 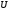 , сторону
, сторону 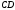 в точці
в точці  З’єднаємо точки
З’єднаємо точки  і
і 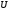 , так як вони лежать в одній площині грані
, так як вони лежать в одній площині грані 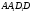 Аналогічно отримуємо
Аналогічно отримуємо 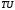 і
і 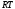 .
. -шуканий переріз.
-шуканий переріз.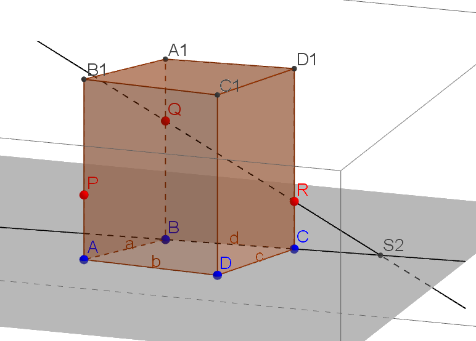


Задача
Побудувати переріз паралелепіпеда
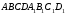 площиною, що проходить через точки
площиною, що проходить через точки 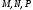 .
.Точки
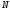 і
і  лежать в площині перетину і в площині нижньої основи паралелепіпеда. Побудуємо пряму, яка проходить через ці точки . Ця пряма є слідом січної площини на площині основи паралелепіпеда.
лежать в площині перетину і в площині нижньої основи паралелепіпеда. Побудуємо пряму, яка проходить через ці точки . Ця пряма є слідом січної площини на площині основи паралелепіпеда.Продовжимо пряму на якій лежить сторона
 паралелепіпеда. Прямі
паралелепіпеда. Прямі  і
і 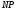 перетнуться в деякій точці
перетнуться в деякій точці 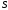 . Ця точка належить площині перерізу.
. Ця точка належить площині перерізу. Так як точка
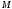 також належить площині перерізу і перетинає пряму
також належить площині перерізу і перетинає пряму 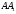 в деякій точці
в деякій точці 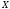 .
.Точки
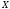 і
і 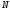 лежать в одній площині на грані
лежать в одній площині на грані 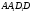 , з’єднаємо їх і отримуємо пряму
, з’єднаємо їх і отримуємо пряму  .
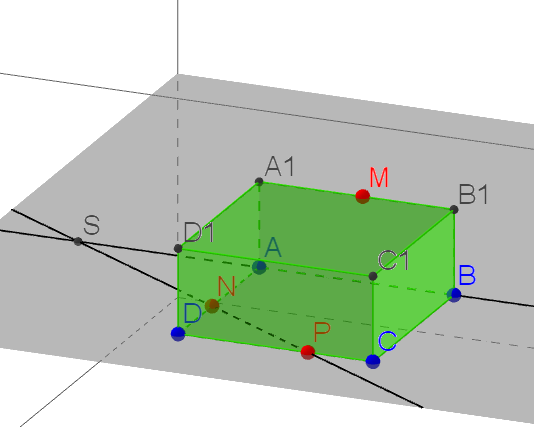
.Так як площини граней паралелепіпеда паралельні, то через точку
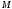 можна провести пряму в грані
можна провести пряму в грані 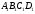 , паралельну прямій
, паралельну прямій 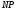 . Ця пряма перетне сторону
. Ця пряма перетне сторону 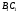 в точці
в точці  .
.Аналогічно проводимо пряму
 , паралельно прямій
, паралельно прямій  . З’єднуємо
. З’єднуємо  з
з  і отримуємо шуканий переріз-
і отримуємо шуканий переріз-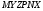 .
.
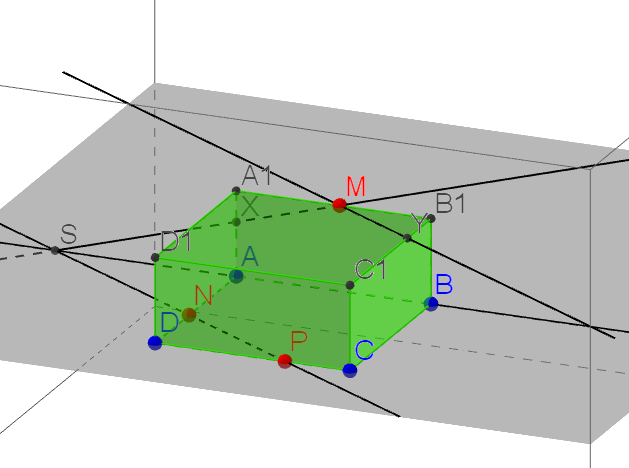
Задача
На ребрах
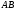 і
і 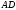 піраміди
піраміди 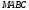 задамо відповідно точки
задамо відповідно точки 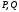 -середини цих ребер, а на ребрі
-середини цих ребер, а на ребрі  задамо точку
задамо точку  . Побудуємо переріз піраміди площиною, що проходить через точки
. Побудуємо переріз піраміди площиною, що проходить через точки 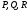 .
.Основним слідом площини
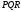 є пряма
є пряма 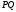 .
.Знайдемо точку
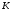 , в якій площину
, в якій площину 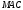 перетинає пряма
перетинає пряма 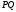 . Точки
. Точки  належать і площині
належать і площині 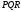 ,і площині
,і площині 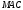 . Тому провівши пряму
. Тому провівши пряму  , ми отримаємо лінію перетину площин.
, ми отримаємо лінію перетину площин.Знайдемо точку
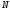 в площині
в площині 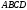 , проведемо пряму
, проведемо пряму 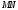 і знайдемо точку
і знайдемо точку 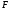 в площині
в площині 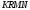 .
.Точка
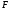 є загальною точкою площин
є загальною точкою площин 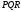 і
і 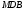 , тобто ці площини перетинаються по прямій , що проходить через точку
, тобто ці площини перетинаються по прямій , що проходить через точку 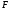 .
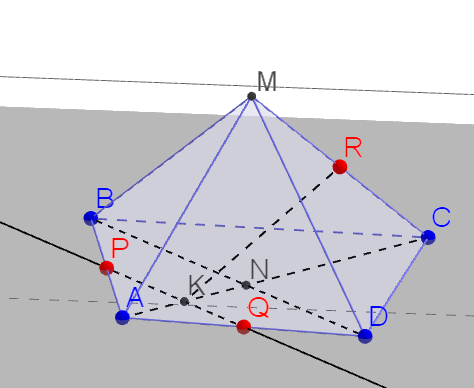
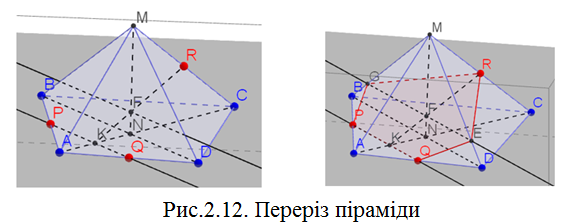
.Подальші побудови зрозумілі з рисунка.Отримуємо
 -шуканий переріз.
-шуканий переріз.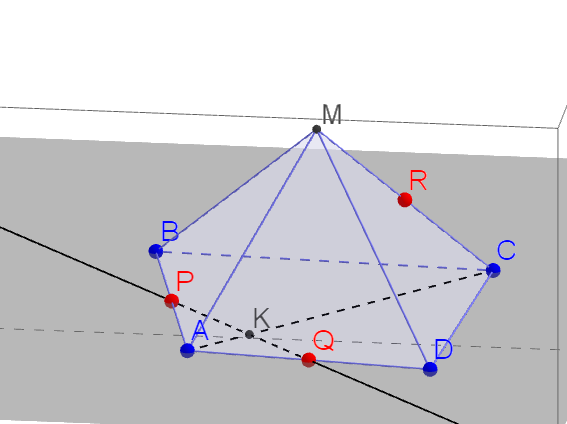
ВИСНОВКИ
Курс «Геометрія» є одним з основних математичних курсів, складових фундаментів математичної підготовки учнів. Складання динамічних креслень в навчанні геометрії має пронизувати всі роки навчання. Оскільки курс стереометрії для розуміння дітей є досить абстрактним і досить складним для сприйняття , то завдання вчителя полягає в тому, щоб зробити вивчення цього навчального матеріалу максимально наочним і зрозумілим.
Одним із шляхів розв’язування даної задачі є використання комп'ютерних технологій, що дозволяє не тільки побачити на екрані динамічну 3D модель, але і розглянути безліч варіацій, як, наприклад, при побудові перерізів різних многогранних фігур. Найкращим чином для цих цілей підходить комп'ютерне середовище GeoGebra з її можливостями [5, c. 80].
Суть методу геометричних перетворень при розв’язуванні геометричних задач на побудову полягає в залученні того чи іншого геометричного перетворення, спираючись на властивості якого задача може бути розв’язана.
Щоб оволодіти вмінням розв’язувати задачі методом перетворень, необхідно виробити у себе такі вміння-компоненти методу:
вміння будувати образи фігур в кожному перетворенні;
вміння бачити відповідні при зазначеному перетворенні точки на відповідних фігурах;
вміння виділяти елементи, що визначають те чи інше перетворення (вісь або центр симетрії, центр і кут обертання, вектор паралельного переносу, центр і коефіцієнт гомотетії);
Важливо враховувати, що при розв’язуванні тієї чи іншої геометричної задачі на побудову вибір відповідного перетворення зумовлює особливостями базової фігури і відносинами між даними і шуканими елементами, пов'язаними з цією фігурою. А правильний вибір призводить, як правило, до раціонального розв’язування задачі. При цьому форма і властивості базової фігури грають в підборі перетворення визначальну роль. Так симетрію слід вводити в тих випадках, коли базова фігура має центр симетрії (паралелограм, коло та ін.) Або вісь симетрії (трикутник, рівнобедрена трапеція, коло та ін.)
Застосування в задачах гомотетії передбачає наявність у двох базових фігур центру гомотетії. Слід враховувати, що в задачах на побудову за допомогою гомотетії або подібності часто застосовується такий прийом: при проведенні аналізу відкидають дані лінійні елементи або нехтують тією чи іншою позицією однієї з даних фігур (як правило, позицією однієї їх точок) і розглядають можливості побудови за знайденими даними фігури, подібної або гомотетичної шуканої фігури, після чого використовують відкинутий елемент, що остаточно визначає шлях побудови.
Отже, бачимо, що застосування методу перетворень при розв’язуванні задач на побудову вимагає ретельного аналізу умов і грамотного підходу до вибору перетворення, з яким не рекомендується поспішати: 1) проаналізувавши умови і вимоги задачі, потрібно виділити базову фігуру; 2) намітивши те чи інше перетворення, перевірити заздалегідь, чи є всі елементи, які задають його; 3) згадати властивості перетворення і прикинути, чи допоможуть вони розв’язати задачу. Тільки після цього слід приступати до розв’язування задачі [4, c. 36].
Для досягнення мети були вирішенні такі завдання:
дослідження вже наявної науково-методичної літератури з цієї теми;
розглянути конструктивні, обчислювальні і анімаційні можливості систем динамічної геометрії, як засіб розв’язування задач на побудову в просторі;
розглянути задачі на побудову перерізів;
Розглянути задачі на геометричні перетворення в просторі;
Поставлена мета дослідження (вивчення різних методів розв’язування задача на побудову в просторі, використовуючи систему динамічної геометрії GeoGebra) була досягнута.
СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ
Наумович Н.В. Простейшие геометрические преобразования в пространстве и задачи на построение. Москва, 1959. 9-56 с.
Понарин Я.П. Стереометрия, преобразования в пространстве. Москва, Издательство МЦНМО,2006. 65 с.
Далингер В.А. Геометрия:стереометрические задачи на построение. Москва, 2019. 54 с.
Метод геометрических преобразований при решении геометрических задач на построение. 1-2 с.
URL:https://referat.bookap.info/work/171304/Metod-geometricheskix- preobrazovanij-pri
Тиличеева И.В. Магистерская диссертация. Методика обучения решению стереометрических задач в 10 классе с использованием систем динамической геометрии. Красноярск, 2019.3 c.
Методика решения задач на построения в стереометрии. URL:http://dodiplom.ru/ready/104561
Решение задач на построение в стереометрии. 14-15 c.
URL:https://infourok.ru/kursovaya-rabota-po-geometrii-na-temu-reshenie-zadach-na-postroenie-v-stereometrii-4055480.html
E.М. Кондрушенко, В.А. Нелюбина. Задачи на построение в пространстве и методика обучения их решению. Великий Новгород, 2016. 5 с.
Танкевич Л.М., Шкляр А.Е. GeoGebra как средство решения стереометрических задач. Молодой ученый, 2018. 53 с.
.
1 2 3 4 5 6