
Перетворення подібності (гомотетія)
Задача
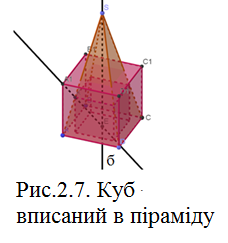
В правильну чотирикутну піраміду вписати куб так ,щоб чотири його ребра знаходились на бічних гранях піраміди.
Аналіз. Припустимо, що задача розв’язана і в піраміду SABCD вписали куб
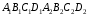 , так що площина його основи
, так що площина його основи 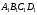 співпадає з площиною основи
співпадає з площиною основи  даної піраміди, а ребра
даної піраміди, а ребра 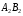 ,
, ,
,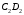 ,
, 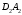 лежать на її бічних гранях. Відмітимо, що
лежать на її бічних гранях. Відмітимо, що 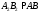 ,
,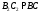 ,
,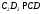 ,
, ,так як кожне з них паралельне площині
,так як кожне з них паралельне площині 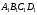 .
. 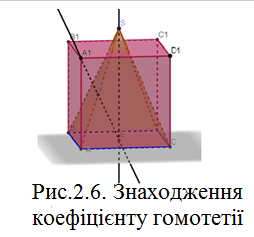 Основа висоти піраміди є центр гомотетії основи піраміди і основи куба, який ми шукаємо. Тоді точка О може бути прийнята за центр гомотетії шуканого та будь-якого допоміжного куба(Рис.2.6). В якості допоміжного куба можна взяти куб, основа якого лежить на площині
Основа висоти піраміди є центр гомотетії основи піраміди і основи куба, який ми шукаємо. Тоді точка О може бути прийнята за центр гомотетії шуканого та будь-якого допоміжного куба(Рис.2.6). В якості допоміжного куба можна взяти куб, основа якого лежить на площині 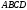 , а сторони основи паралельні сторонам
, а сторони основи паралельні сторонам 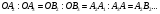
 ,
,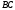 ,
,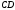 ,
,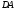 основи піраміди. При цьому центрі основи повинні збігтись.
основи піраміди. При цьому центрі основи повинні збігтись. Якщо ми будуємо в просторі, за основу допоміжного куба можна взяти основу піраміди
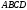 . Основа куба лежить на площині
. Основа куба лежить на площині 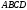 симетрично цій грані (
симетрично цій грані (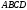 ), а це означає, що центри нижніх граней співпадуть. Значить цю точку можна взяти за центр гомотетії( т. Е). Вершину
), а це означає, що центри нижніх граней співпадуть. Значить цю точку можна взяти за центр гомотетії( т. Е). Вершину 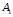 ми повинні перенести на ребро
ми повинні перенести на ребро 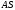 піраміди. Так як точка Е –центр гомотетії, то вона «піде» по прямій
піраміди. Так як точка Е –центр гомотетії, то вона «піде» по прямій 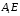 , а це означає ,що точка
, а це означає ,що точка 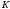 - це точка перетину
- це точка перетину 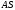 з
з 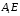 . Для інших вершин (ребер) нічого будувати не потрібно, так як піраміда правильна. В результаті отримаємо куб
. Для інших вершин (ребер) нічого будувати не потрібно, так як піраміда правильна. В результаті отримаємо куб 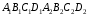 , коефіцієнт гомотетії
, коефіцієнт гомотетії  [1, c. 40].
[1, c. 40].  Побудова. Будуємо куб
Побудова. Будуємо куб 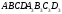 , так щоб точки
, так щоб точки  лежали по ту сторону площини
лежали по ту сторону площини 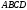 , що і вершина
, що і вершина 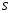 піраміди. Далі з’єднаємо відрізком прямої точки О і
піраміди. Далі з’єднаємо відрізком прямої точки О і 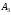 . Пряма
. Пряма 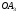 перетинається з ребром
перетинається з ребром 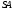 в точці
в точці 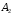 , яка буде однією із вершин шуканого кубу . Для знаходження вершин
, яка буде однією із вершин шуканого кубу . Для знаходження вершин 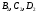 кубу треба провести прямі
кубу треба провести прямі 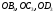 і знайти точки їх перетину відповідно з прямими
і знайти точки їх перетину відповідно з прямими 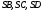 .
. З отриманих точок
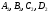 на площину
на площину 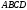 треба опустити перпендикуляри, основи яких
треба опустити перпендикуляри, основи яких  і будуть іншими вершинами кубу, який шукаємо(Рис.2.7 а)
і будуть іншими вершинами кубу, який шукаємо(Рис.2.7 а)Але якщо ми будуємо в просторі, є інший алгоритм побудови :
Будуємо чотирикутник
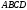 . Знаходими його центр – точка Е(точка перетину діагоналей, в нашому випадку –це центр гомотетії).
. Знаходими його центр – точка Е(точка перетину діагоналей, в нашому випадку –це центр гомотетії). Через точку Е проводимо пряму, яка перпендикулярна площині
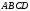 . На цій прямій вибираємо довільну точку S (вершина нашої піраміди).
. На цій прямій вибираємо довільну точку S (вершина нашої піраміди).Будуємо піраміду. Далі будуємо допоміжний куб, який «стоїть» на основі піраміди
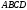 .
. Через вершину куба
Через вершину куба 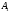 та точку Е проводимо пряму, для того щоб знайти точку перетину з ребром AS (точка К). Точка К є вершиною шуканого кубу . Для інших вершин (ребер) нічого будувати не потрібно, так як піраміда правильна .
та точку Е проводимо пряму, для того щоб знайти точку перетину з ребром AS (точка К). Точка К є вершиною шуканого кубу . Для інших вершин (ребер) нічого будувати не потрібно, так як піраміда правильна . Будуємо куб, який шукали (Рис.2.7 б).
При змінні положення вершини піраміди, змінюється коефіціїєнт гомотетії, а центр гомотетії нерухомий, тим самим ми беремо різні правильні піраміди .Основа куба не обов’язково повинна співпадати з основою піраміди . Головне, щоб у них був спільний центр гомотетії.
Доведення. Так як
 , то
, то 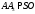 , з цього випливає що прямі
, з цього випливає що прямі 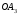 і
і 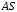 лежать в одній площині , і тому перетнуться в деякій точці
лежать в одній площині , і тому перетнуться в деякій точці 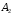 . Ця точка і буде однією з вершин шуканої фігури . Аналогічно, прямі
. Ця точка і буде однією з вершин шуканої фігури . Аналогічно, прямі 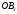 , і
, і  ,
,  і
і 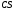 ,
, і
і 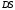 також перетинаються . Із побудови випливає , що
також перетинаються . Із побудови випливає , що 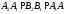 і т.д.
і т.д.Розглянемо відповідні подібні трикутники, отримаємо:
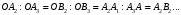 Но так як
Но так як  з цього випливає
з цього випливає 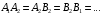 , фігура
, фігура  є куб , основа якого лежить на основі піраміди, а сторони верхньої основи знаходяться на бічних гранях піраміди . Таким чином, побудований куб –шуканий.
є куб , основа якого лежить на основі піраміди, а сторони верхньої основи знаходяться на бічних гранях піраміди . Таким чином, побудований куб –шуканий.Дослідження. Задача має єдиний розв’язок, так як прямі
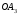 і
і 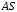 завжди перетинаються в одній точці . Якщо в якості допоміжного куба взяти інший куб, наприклад,
завжди перетинаються в одній точці . Якщо в якості допоміжного куба взяти інший куб, наприклад, 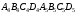 ,який розташований відповідним чином, то вершина
,який розташований відповідним чином, то вершина  лежала би на тій же прямій
лежала би на тій же прямій 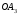 і відповідно положення шуканого куба не зміниться.
і відповідно положення шуканого куба не зміниться. Задача
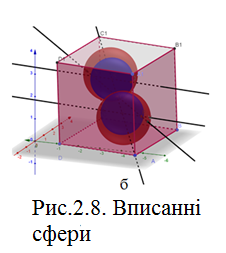
У два протилежних тригранних кута даного куба вписати дві рівні сфери так, щоб кожна з них дотикається трьох граней і в той же час, щоб сфери дотикаються один одного.
Аналіз. Дану задачу можна розв’язати з точки зору гомотетії. Нехай задача розв’язана, і в куб вписали дві рівні сфери так, що кожна з них дотикається трьох граней і в той же час, сфери дотикаються один одного.
Знайдемо центр гомотетії. Центром гомотетії буду точка дотику сфер (точка
 - це точка перетину діагоналей куба). В точці перетину діагоналі діляться навпіл (Рис.2.8 а) Тому, коли ми будуємо в просторі нам достатньо провести одну діагональ куба( в нашому випадку
- це точка перетину діагоналей куба). В точці перетину діагоналі діляться навпіл (Рис.2.8 а) Тому, коли ми будуємо в просторі нам достатньо провести одну діагональ куба( в нашому випадку 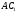 ) та знайти її середину – це і буде центром гомотетії. Коефіцієнт гомотетії
) та знайти її середину – це і буде центром гомотетії. Коефіцієнт гомотетії 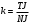 .
. Тепер треба знайти центри сфер
Тепер треба знайти центри сфер  . Нехай сфера з центром
. Нехай сфера з центром 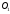 дотикається граней
дотикається граней 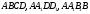 відповідно сфера з центром в точці
відповідно сфера з центром в точці 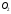 дотикається граней
дотикається граней 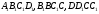 .Так як перша сфера дотикається граней
.Так як перша сфера дотикається граней 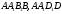 , то її центр
, то її центр 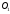 рівновіддалений від зазначених граней, тобто лежить бісекторній площині двогранного кута з ребром
рівновіддалений від зазначених граней, тобто лежить бісекторній площині двогранного кута з ребром 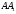 , тобто на площині
, тобто на площині 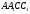 (з урахуванням того, що
(з урахуванням того, що  -куб).
-куб). Так як перша сфера дотикається граней
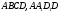 , то її центр рівновіддалений від зазначених граней, тобто лежить бісекторній площині двогранного кута з ребром
, то її центр рівновіддалений від зазначених граней, тобто лежить бісекторній площині двогранного кута з ребром 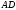 . Тоді точка
. Тоді точка 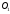 лежить на прямій перетину площин
лежить на прямій перетину площин 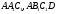 ,тобто на
,тобто на 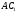 (сфера знаходиться всередині куба , тоді
(сфера знаходиться всередині куба , тоді 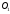 -точка відрізка
-точка відрізка 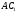 ). Аналогічно, що точка
). Аналогічно, що точка 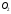 - лежить на відрізку
- лежить на відрізку 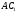 ).
).Побудова
 Будуємо відрізок
Будуємо відрізок  - радіус сфери.
- радіус сфери. Будуємо куб
 .
. Будуємо
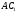 - діагональ куба. Знаходимо середину цієї діагоналі (точка
- діагональ куба. Знаходимо середину цієї діагоналі (точка 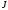 ).
). На діагоналі
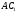 відмічаємо центри сфер
відмічаємо центри сфер  (сфери рівні за умовою). Будуємо дані сфери.
(сфери рівні за умовою). Будуємо дані сфери. Через центри сфер
 проводимо паралельні прямі. Через точку дотику сфер проводимо пряму , яка перетинає грані
проводимо паралельні прямі. Через точку дотику сфер проводимо пряму , яка перетинає грані 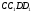 ,
,  куба в точках
куба в точках 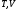 .
. Далі знаходимо точки перетину прямої з паралельними прямими (точки
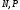 ). Так як ми будуємо в просторі , ми використаємо гомотетію відносно точки. Центром гомотетії є точка
). Так як ми будуємо в просторі , ми використаємо гомотетію відносно точки. Центром гомотетії є точка 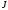 (точка дотику сфер), коефіцієнт гомотетії
(точка дотику сфер), коефіцієнт гомотетії 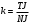 . Аналогічно будуємо другу сферу.
. Аналогічно будуємо другу сферу.Задача
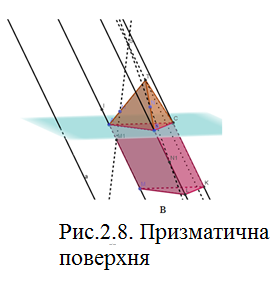
Піраміду
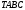 перетворити в призматичну поверхню, бічні ребра якої паралельні даній прямій
перетворити в призматичну поверхню, бічні ребра якої паралельні даній прямій  , так щоб відрізок
, так щоб відрізок 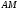 ребра
ребра 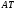 перетворився в рівний йому відрізок відповідного ребра призматичної поверхні.
перетворився в рівний йому відрізок відповідного ребра призматичної поверхні. Аналіз. Площину основи піраміди візьмемо за осьову площину гомології та через вершину піраміди
 проведемо пряму
проведемо пряму 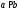 .
. Вершині піраміди
Вершині піраміди  поставимо у відповідність нескінченно віддалену точку
поставимо у відповідність нескінченно віддалену точку 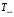 прямої
прямої 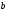 . Тоді всі бічні ребра
. Тоді всі бічні ребра 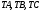 перейдуть в паралельні прямі
перейдуть в паралельні прямі 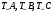 . Точки
. Точки  як належали осевій площині гомології залишаться незмінними.
як належали осевій площині гомології залишаться незмінними. Для знаходження центру гомології
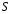 треба на прямій
треба на прямій 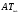 відкласти від точки
відкласти від точки 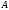 відрізок
відрізок 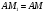 . Точки
. Точки 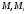 будемо вважати відповідними. Центр гомології
будемо вважати відповідними. Центр гомології 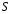 буде знаходитись в точці перетину прямих
буде знаходитись в точці перетину прямих 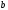 і
і 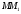 . Ці прямі перетнуться, так як знаходяться в одній площині. Кожній точці поверхні піраміди буде відповідати відповідна точка призматичної поверхні [1, c. 31].
. Ці прямі перетнуться, так як знаходяться в одній площині. Кожній точці поверхні піраміди буде відповідати відповідна точка призматичної поверхні [1, c. 31].Побудова
Будуємо піраміду
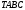 , відрізок
, відрізок 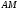 і пряму
і пряму 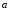 .
.Через вершину
 проводимо пряму
проводимо пряму 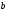 , яка паралельна прямій
, яка паралельна прямій 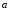 .
.Через вершини піраміди
 проводимо прямі , які паралельні прямій
проводимо прямі , які паралельні прямій 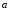 .
.Для знаходження центру гомотетії, на прямій
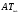 відкладемо від точки
відкладемо від точки 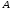 відрізок
відрізок 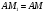 .
.Центр гомотетії
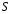 буде знаходитись в точці перетину прямих
буде знаходитись в точці перетину прямих 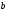 і
і 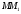
Таким чином, піраміда
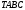 перетвориться в призматичну поверхню, бічні ребра якої паралельні заданому напрямку
перетвориться в призматичну поверхню, бічні ребра якої паралельні заданому напрямку 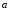 , а відрізок
, а відрізок 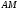 ребра
ребра 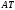 перетворюється в рівний йому відрізок
перетворюється в рівний йому відрізок 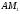 .
.1 2 3 4 5 6