РОЗДІЛ 1
ТЕОРЕТИЧНІ ОСНОВИ ГЕОМЕТРИЧНИХ ПОБУДОВ У КУРСІ СТЕРЕОМЕТРІЇ
Геометричні побудови в просторі
Більшість задач курсу зводяться до вирішення планіметричних задач, відповідно всі недоліки, що мали місце при вивченні планіметрії, відчуваються і при вивченні стереометрії.
Отже, для успішного вивчення стереометрії треба постійно повертатися до планіметричного матеріалу; перед вивченням тієї чи іншої теореми необхідно повторювати потрібні планіметричні відомості.
У стереометрії принципово інший підхід до геометричних побудов.
Якщо при вивченні планіметрії учні користуються ілюстраціями, які дають явні уявлення про досліджувальний об'єкт, то в стереометрії немає креслярських інструментів, які дозволяють зобразити просторові фігури. Тут ми маємо справу не з самим об'єктом, а лише з його зображенням.
Кожна стереометрична задача є одночасно задачою на побудову зображення фігури за допомогою властивостей паралельної проекції. Це вимагає від учнів значно більших зусиль, ніж їх потрібно при вирішенні планіметричних задач.
3. Курс стереометрії будується аксіоматично. При вивченні аксіоматики стереометрії необхідно вирішити дві основні методичні задачі:
1)переформульовуються аксіоми планіметрії для простору (деякі повинні бути з уточненнями).
2) додаються нові аксіоми простору, які на перших етапах вивчення ілюструються за допомогою моделей, стереометричного ящика, малюнка, геометрії класної кімнати.
Формування просторових уявлень йде в кілька етапів і включає в себе:
• вміння уявити за кресленням цілісний образ геометричної фігури, взаємне розташування її елементів;
• вміння мислено змінити положення фігури – подивитися з іншого боку;
• вміння мислено розбити фігуру, скласти з неї новий об'єкт;
• вміння уявити фігуру на основі її словесного опису.
Стереометричні задачі на побудову можна розв’язувати на проекційному кресленні, в уяві та за допомогою спеціальної системи динамічної геометрії (GeoGebra).
Геометричні побудови на проекційному кресленні отримують в результаті паралельного або центрального проектування.Тому зображення(креслення) називають проекційним кресленням [7, c. 14-15].
Проекційне креслення-це креслення, яке будується, стосовно до школи, за законами вільної паралельної проекції.
Значну увагу при розв’язуванні стереометричних задач на побудову треба приділяти і задачам на «уяву» побудови. Здібність уявляти геометричні об’єкти в різних розташуваннях ,визначати чи перетинаються вони, дотикаються або в них немає спільних точок, мислено знаходити лінію їх перетину, якщо вона є, - все це допомагає розвити просторове уявлення учнів [8, c.5].
При уявних побудовах, роль креслення зовсім інша. Якщо на проекційному кресленні можна робити відповідні побудови та знаходити шукані елементи, то при уявній побудові кресленню відводиться не головне місце. Всі побудови здійснюються уявно, і креслення грає тільки допоміжну, ілюстративну ролі.
В даний час створено значну кількість програмних засобів, що дають змогу учням будувати зображення геометричних тіл (3dMAX, Maple, Blender, Foss Lviv Lightwave 3D та ін). Використання цих програмних продуктів направлено головним чином на реалізацію принципу наочності, який є одним з провідних дидактичних принципів.
Однією із найбільш вдалих серед таких програм, на нашу думку є GeoGebra. Це вільне програмне забезпечення, призначене для моделювання як планіметричних, так і стереометричних фігур, дослідження їх властивостей залежно від зміни параметрів. GeoGebra дає змогу будувати графіки функцій, фігури за їх рівняннями; особливістю даної програми є те, що всі елементи, побудовані в її середовищі, є динамічними і можуть бути змінені всього в 2-3 кліки. Крім того, програма GeoGebra дає змогу виконувати різні обчислення, наприклад, можна знайти площу фігури, обчислити інтеграл або досліджувати якусь функцію
Таким чином GeoGebra - це не просто барвиста ілюстрація до уроку математики, це перш за все потужний інструмент, який дозволяє організувати дослідницьку роботу учнів, використовуючи GeoGebra безліч тем зі шкільного курсу математики вийти перетворити в невелику дослідницьку роботу, яку зможуть провести учень за невеликий час на своєму уроці.
Можна висунути гіпотезу і за допомогою побудов і динамічних можливостей програми перевірити її. Такий момент ми будемо називати - комп'ютерний експеримент. Такі комп'ютерні експерименти з використанням програми GeoGebra на уроках математики можуть допомогти учням краще засвоїти матеріал і розвинути просторове мислення [9, c. 53].
В чому полягає зміст розв’язування задачі на побудову?
Розв’язати задачу на побудову – означає по даному геометричному образу побудувати інший геометричний образ.Це може бути виконано різними методами, наприклад, метод геометричних місць та за допомогою геометричних перетворень.
Застосування геометричних перетворень при розв’язуванні задач на побудову складається в наступному: якщо фігуру
, яка задана за умовою задачі, треба побудувати, то спочатку будують перетворену фігуру 
, яку легше побудувати, а потім за допомогою зворотного перетворення будують шукану фігуру.Коли треба розв’язати більш складну задачу на побудову, з’являється необхідність згадати: як знайти метод розв’язування задачі, як знайти всі можливі розв’язки задачі, як визначити умови можливості її розв’язання. При розв’язуванні планіметричних задач на побудову часто рекомендують використовувати схему розв’язування, яка складається з чотирьох етапів:
аналіз; 2) побудова; 3) доведення; 4) дослідження. Цю схему можна використовувати при розв’язуванні стереометричних задач на побудову .
Кожний етап схеми має свою мету.
Аналіз. Мета аналізу полягає в пошуку такого зв’язку між елементами фігури, яку шукаємо та даними задачі, який допоміг би побудувати шукану фігуру. Рекомендується зробити схематичне креслення, в якому би були задіяні дані, шукані елементи та шукана фігура. Дивлячись на це креслення і уявляючи цю фігуру в просторі, помічають, що для побудови шуконой фігури треба зробити ті чи інші перетворення або побудови. Після певного числа побудов можна прийти к фігурі, яку ми вже знаємо.
Побудова. Ця частина розв’язування полягає у послідовності головних операцій, які необхідно виконати для побудови шуканої фігури. Якщо задача розв’язується на проекційному кресленні, тоді в подальшому вона повинна бути оформлена графічно за допомогою креслярських інструментів. Якщо задача розв’язується уявно або за допомогою програми GeoGebra, достатньо перечислити ті побудови, які необхідні для її розв’язання. Фактично це буде план розв’язання, але цього часто буває достатньо і їм можна обмежитись.
Доведення. Цей етап розв’язування ставить за мету, показати, що побудована фігура задовольняє всім умовам задачі.
Дослідження. Задача вважається розв’язаною, якщо ми отримали деяку фігуру, яка задовольняє всім умовам задачі. Но може так трапитись, що умові задачі задовольняє не тільки ця фігура, але ще одна фігура або декілька таких фігур. Дослідження повинно установити кількість фігур, які задовольняють умовам задачі. Треба встановити скільки розв’язків має задача. Крім того, треба встановити чи є такі випадки, які можуть з’явитися при певному розташуванні елементів, їх величин, коли необхідні побудови неможливі. Треба встановити, чи існують в цих випадках розв’язки, та знайти їх .
Для цього треба уважно подивитися усі побудови, з яких складається розв’язування, і в кожному випадку з’ясувати, чи завжди цю побудову можна виконати і якщо да, то як і скількома способами [1, c. 12-15].
Перенесення, центральна, осьова і дзеркальна симетрії простору
Визначення руху та рівних фігур. Рухом простору називається відображення простору на себе, при якому зберігаються відстані між точками: якщо
і 
- будь-які дві точки простору, а 
і 
- їх образи, то 
. З цієї умови випливає, що образи двох різних точок різні, т. е. рух є оборотне відображення простору на себе і тому є перетворенням простору.Фігура
називається рівною (конгруентною) фігурі 
, якщо існує рух 
, яке відображає на : 
. Ясно, що ставлення рівності фігур рефлексивно, симетрично і транзитивно, це є відношенням еквівалентності.
Перенесення. Перенесенням 
простору на вектор 
називається перетворення, при якому кожна точка 
відображається на таку точку
, що
, де 
- заданий вектор. Так як для будь-яких двох точок і і їх образів і , то перенос є рух простору (Рис.1). 
Центральна симетрія. Симетрією щодо точки O (центральною симетрією) 
простору називається перетворення простору, яке точку 
відображає на себе, а будь-яку іншу точку 
відображає на таку точку 
, що точка є серединою відрізка 
(Рис.2). Легко бачити, що центральна симетрія простору є рухом. 
для будь-яких двох точок 
і 
і їх образів 
і 
, 
. Осьова симетрія. Симетрією простору щодо даної прямої
(осьовою симетрією) 
називається перетворення, яке кожну точку прямої відображає на себе, а будь-яку іншу точку 
простору відображає на таку точку 
, що пряма служить серединним перпендикуляром до відрізка . Пряма називається віссю симетрії [2, c. 183].Дзеркальна симетрія. Симетрією простору щодо даної площини
(дзеркальною симетрією 
) називається перетворення простору, при якому кожна точка площини відображається на себе, а будь-яка інша точка переходить в таку точку , що площина перпендикулярна до відрізка і ділить його навпіл. Площина називається площиною симетрії.Подання перенесення композиціями дзеркальних і осьових симетрій.
Композиція дзеркальних симетрій щодо двох паралельних площин є перенесення простору, вектор якого перпендикулярний цим площинам, спрямований від площини першої симетрії до площини другої симетрії і має модуль, рівний подвоєній відстані між площинами. Всяке перенесення простору представимо такою композицією, при цьому одна з площин симетрії може бути будь-якою площиною, перпендикулярною вектору переносу.
Композиція осьових симетрій щодо двох паралельних прямих є перенесення простору, вектор який перпендикулярний цим прямим, спрямований від осі першої симетрії до осі другий симетрії і має модуль, рівний подвоєній відстані між осями. Всяке перенесення простору може бути представлено такою композицією, при цьому одна з осей може бути будь-якою прямою, перпендикулярною вектору переносу.
Загальні властивості рухів простору
Два роду рухів простору. Нехай дано тетраедр
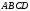. Можливі два і тільки два випадки: упорядкована трійка (
,
,
) векторів є позитивно орієнтованою (правою) або ж вона є негативно орієнтованою (лівою). Кажуть що в першому випадку тетраедр 
орієнтований позитивно, а у другому - він орієнтований негативно. Орієнтація тетраедра істотно залежить від порядку записи його вершин.Можна довести, що якщо під час руху простору деякий тетраедр і його образ мають однакову орієнтацію, то це властивість має місце для будь-якої пари відповідних при цьому русі тетраедрів. У цьому випадку рух простору називається рухом першого роду. Якщо ж рух відображає певний тетраедр на тетраедр протилежної орієнтації, то цим властивістю володіє будь-яка пара відповідних при цьому руху тетраедрів, такий рух простору називається рухом другого роду.
Порівнянням орієнтації тетраедра і його образу виявляємо, що перенос і осьова симетрія простору є рухами першого роду (хоча осьова симетрія площині - рух другого роду), а центральна і дзеркальна симетрії простору - руху другого роду (проте центральна симетрія площині - рух першого роду [2, c.185].
Інваріанти рухів простору. Для рухів простору зберігає силу теорема про спосіб прямої при рухах площині разом з її доказом: рух відображає кожну пряму на пряму.
Теорема 1. Рух простору відображає кожну площину на площину.
При будь-якому перетворенні перетину множин є перетин їх образів.
Зокрема, під час руху простору пряма перетину площин відображається на пряму перетину їх образів. При перенесенні і центральної симетрії площина відображається або на паралельну їй площину, або на себе, при цьому на себе відображається кожна площина, паралельна вектору переносу і кожна площина, яка містить центр симетрії.
Осьова симетрія відображає на себе кожну площину, яка містить її вісь, і кожну площину, перпендикулярну осі. Дзеркальна симетрія, крім площині симетрії, відображає на себе кожну площину, перпендикулярну площині симетрії.
Теорема 2. Рух простору зберігає паралельність прямих, паралельність площин і паралельність прямої і площини.
Справді, образи двох паралельних прямих лежать в одній площині і не можуть перетинатися, так як інакше точка перетину не мала б свого прообразу. До цього ж протиріччя приходимо при припущенні перетину образів двох паралельних площин або образів паралельних прямої і площини. Оскільки рух зберігає відношення «лежати між» для трьох точок прямої, т. е. зберігає порядок точок на прямій, то має місце теорема:
Теорема 3. Рух простору відображає відрізок на відрізок, промінь на промінь, напівлощина на напівплощину, півпростір на півпростір.
З визначення руху та визначення конгруентних фігур слідує теорема:
Теорема 4. Рух простору зберігає величину кута між прямими, величину кута між площинами і величину кута між прямою і площиною[2, c.187].
Справді, кут між образами двох перетинаючих прямих дорівнює куту між цими прямими за визначенням рівних (конгруентних) фігур. Кут між мимобіжними прямими визначається через кут між пересічними прямими і паралельність прямих, а тому також інваріантний при рухах. Зокрема, зберігається перпендикулярність прямих. Звідси випливає инваріантність кута між площинами і кута між прямою і площиною. Зокрема, зберігається перпендикулярність двох площин, прямої та площини.
Поворот простору навколо осі
Поворот як частинний вид руху. Не існує повороту простору біля точки з тієї причини, що немає розумного способу встановлювати напрямок такого повороту. Однак можна природним чином ввести поняття повороту навколо орієнтованої прямої(Осі).
Означення. Поворотом
простору навколо осі осі 
на заданий орієнтований кут 
називається таке перетворення простору, при якому в кожній площині , перпендикулярній прямій 
, індукується поворот на кут 
біля точки її перетину з прямою 
(Рис.3).Осьова симетрія
уявляє собою частковий вид повороту - поворот на 
.Орієнтація прямої
(вісь повороту) дозволяє однозначно орієнтувати кути в кожній площині, перпендикулярній [2, c. 188]. Теорема. Поворот простору навколо осі є рух (першого роду).
Ознака повороту. Якщо безліччю нерухомих точок руху простору є пряма, то вона є поворотом навколо цієї прямої. Подання повороту композиціями симетрій. Розглянемо композицію
двох дзеркальних симетрій відносно площин 
і 
, які перетинаються, 
. Всі точки прямої нерухомі при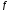 
. При розгляданні образу 
довільної точки 
, тоді кут дорівнює подвійному орієнтованому куту між площинами і .Композиція двох дзеркальних симетрій щодо двох площин, які перетинаються, є поворот навколо прямої їх перетину на подвоєний орієнтований кут між площинами. Навпаки, будь-який поворот простору може бути представлений такою композицією (нескінченно багатьма способами).
Зокрема, осьова симетрія простору є комутативна композиція двох дзеркальних симетрій, площини яких перпендикулярні і містять вісь симетрії.
Далі розглянемо композицію
двох осьових симетрій, осі 
і 
яких перетинаються в точці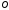 
. Проведемо перпендикуляр к площині 
в точці 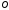. Представимо 
і 
композиціями дзеркальних симетрій: 
, 
. Знаходимо: 
, тоді 
Таким чином, композиція двох осьових симетрій щодо прямих, які перетинаються, є поворот простору навколо перпендикулярної їм прямої, проходить через точку їх перетину, на подвоєний орієнтований кут між осями даних симетрій. Навпаки, всякий поворот простору можна представити (різними способами) композицією двох осьових симетрій. Їх осі перпендикулярні осі повороту, перетинається на ній і утворюють між собою (орієнтований) кут, рівний половині кута повороту.
Гомотетія простору
Гомотетія площини зберігає силу і для гомотетії простору. Саме, залишаються без зміни визначення гомотетії з поправкою на безліч точок простору, теорема про спосіб прямої, способи завдання гомотетії і побудови образу точки, теорема про композиції двох гомотетій. Додатково до цього необхідна теорема про образ площини.
Гомоте́тія — перетворення, за якого кожній точці площини (простору) ставиться відповідно інша точка (образ даної), що лежить на прямій, яка з'єднує дану точку з якоюсь фіксованою точкою (центром).
Гомотетією з центром
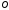{\displaystyle O} і коефіцієнтом {\displaystyle k} 
називають перетворення площини (або простору), що переводить точку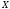
в точку 
таким чином, що 
{\displaystyle {\overrightarrow {OX'}}=k{\overrightarrow {OX}}}. Гомотетію з центром 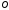і коефіцієнтом 
часто позначають через 
Теорема 1. Площина, яка не містить центр гомотетії, відображається гомотетією на паралельну їй площину. Площина, що містить центр гомотетії, відображається на себе [2, c. 219].
{\displaystyle H_{O}^{k}}Істотною відмінністю гомотетії простору від гомотетії площини є той факт, що гомотетія простору
при 
є перетворенням першого роду, а при 
- перетворенням другого роду, тоді як будь-яка гомотетія площини є перетворення першого роду.В силу інваріантності величини кута між прямими при гомотетії простору будуть інваріантні, перпендикулярність прямої і площини, величина кута між двома площинами, зокрема, перпендикулярність двох площин. Так як при гомотетії відстані між точками множаться на постійне число
, то образом сфери є сфера, образ кола - коло (як перетин сфери і площини). Теорема 2. Будь-які дві нерівні сфери є відповідними при двох гомотетіях (гомотетичні двічі).
Інваріанти простору
Перетворення простору називається перетворенням подібності, або подобою, якщо
(Позитивне) число, для будь-яких двох точок
і 
і їх образів 
і 
при цьому у перетворенні виконується рівність 
, де - постійна.зване коефіцієнтом подібності. Зокрема, при 
подібність є рухом. Гомотетія з коефіцієнтом є подібність з коефіцієнтом .Як і в планіметрії , подібність
простору можна уявити композицією гомотетії 
і руху :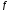 
.Властивості (інваріанти) подібного простору.
1. При подібності пряма відображається на пряму, відрізок на відрізок , промінь на промінь, площина на площину, напівплощина на напівплощину.
2. Подібність зберігає величину кута між прямими, між прямою і площиною, між двома площинами.
3. Подібність зберігає відношення будь-яких двох відрізків. (Це - прямий наслідок з визначення подібності) [2, c. 222].
4. Якщо тіло
-образ тіла 
при подібності ,тоді 
.Для подібності площини доводиться теорема о заданні подібності простору: якщо задані два тетраєдра
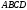і 
такі, що 
,
,
, 
,
,
, то існує одна подібність простору , при якому 
.Паралельний перенос
Розглянемо гомологію з нескінченно віддаленим центром
та нескінченно віддаленою віссю площини гомології 
. Така гомологія є паралельним переносом. 
Нехай нам дані дві відповідні точки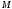 
і (Рис.4). В такому випадку гомологія визначена, так як ми маємо центр гомологіїї (лежить в нескінченності), осьова площина гомології (нескінченно віддалена) і дві відповідні точки. Для побудови точки, яка відповідає будь-якій точці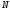 
деякої фігури 
, треба з’єднати точки 
і 
та через точку провести пряму, яка відповідає прямій 
. Пряма 
паралельна прямій та буде відповідною. Далі, через точку
і центр гомології проводимо пряму, яка буде паралельна прямій 
. При перетині її з прямою отримаємо точку 
, яка відповідна точці . Тоді 
, при даному перетворенні зберігається рівність та паралельність відрізків. Кожна фігура перетворюється в рівну фігуру, яка перенесена в нове положення. При цьому всі її точки переміщаються по паралельним прямим. Це перетворення є паралельним переносом, при якому всі точки простору
, ,
… переходять в точки 
,
,
…, цього ж простору таким чином, що 
,всі відрізки, які з’єднують відповідні точки, паралельні , однаково направлені і рівні за величиною [1, c. 28].Якщо через всі точки фігури
провести в одному напрямку паралельні прямі і відкласти на них довільні, но рівні між собою відрізки, то кінці цих відрізків утворюють нову фігуру 
, яка рівна фігурі .Паралельний перенос можна розглядати як частковий випадок гомотетії, коли центр гомотетії є нескінченно віддалена точка.
При розв’язуванні задач на побудову інколи приходиться прибігати к паралельному переносу. Буває, що побудова шуканої фігури викликає труднощі від того, що окремі її частини розташовані на певній відстані один від одного. В такому випадку рекомендується будь-яку частину шуканої фігури перенести деякому напрямку на таку відстань, щоб легше було побудувати всю фігуру. Напрямок переносу залежить від умови задачі, але його треба вибирати так, щоб в побудовану фігуру ввійшло якомога більше даних . Після побудови допоміжної фігури роблять зворотній перенос і тоді отримаємо шукану фігуру. Метод паралельного переносу спрощує розв’язування багатьох задач.
Переносна і поворотна симетрії
Переносна симетрія. Композиція дзеркальної симетрії 
та переносу 
паралельно площині симетрії комунікативна (Рис.5): 
. Її називають переносною симетрією 
простору. Властивості переносної симетрії:
1. Переносна симетрія простору є рухом другого роду (як композиція руху другого роду і руху першого роду).
2. Переносна симетрія не має нерухомих точок.
3. Будь-який відрізок
, що з'єднує точку, що не лежить в площині 
симетрії, з її образом, ділиться площиною симетрії навпіл.4. Кожна площина, паралельна вектору
переносній симетрії і перпендикулярна площині симетрії, інваріантна (нерухома). У ній індукується переносна симетрія 
площини, віссю якої служить пряма 
перетин площин.Більш глибокі властивості переносної симетрії містяться в двох наступних теоремах.
Теорема 1. Композиція осьової і дзеркальної симетрій, у яких відповідно вісь і площина паралельні, є переносна симетрія простору.
Теорема 2 (зворотна). Переносна симетрія простору представимо композицією осьової і дзеркальної (дзеркальної і осьової) симетрії, вісь і площина яких паралельні.
П
оворотна симетрія. Композиція дзеркальної симетрії та повороту 
біля осі, перпендикулярної площини симетрії, комутативна (Рис.6). 
. Ця композиція називається поворотною симетрією з віссю на кут відносно площини 
. Відрізок , який з’єднує точку з її образом при поворотній симетрії , ділиться площиною симетрії навпіл. Точка
-єдина нерухома точка поворотної симетрії. Вона називається центром поворотної симетрії . В окремому випадку, коли
, поворотна симетрія є центральною симетрією 
з центром .Тоді площина і вісь втрачають своє значення: ними можуть бути будь-яка пара перпендикулярних площин і прямих, що містять центр. Поворотна симетрія - рух другого роду [2, c. 190].Теорема. Поворотна симетрія є композиція центральної симетрії і повороту біля осі, що проходить через її центр, і назад.
Більшість задач на побудову в просторі розв’язуються за допомогою перетворення симетрії: вважають, що задача розв’язана і одну точку (пряму або геометричну фігуру), яка симетрична відносно певної площини або площини, яка проходить через відому точку або пряму. Потім цю симетричну точку (пряму або фігуру) підпорядковують тим умовам, яким повинна задовольняти замінна точка (пряма або фігура). Ми отримаємо нову задачу, яку розв’язуємо будь-якими вже відомими способами. Нова задача повинна бути легше заданої задачі. В окремих випадках необхідно переходити к початковим умовам задачі.
Метод ГМТ в стереометричних задачах на побудову
Нагадаємо, що геометричним місцем точок (ГМТ) простору, які володіють даними властивостями, називається безліч всіх точок простору, кожна з яких володіє цією властивістю. Всі інші точки простору зазначеною властивістю не володіють. ГМТ задається властивістю точок, яке називається характеристичною властивістю цього ГМТ (фігури).
Кожна задача, в якій потрібно знайти ГМТ по його характеристичній властивості, передбачає описати це ГМТ наочно через відомі елементарні фігури. Розв’язання задачі на відшукання ГМТ неминуче призводить до доведення двох тверджень - прямого і йому протилежного: необхідно довести, що 1) кожна точка передбачуваного (шуканого) ГМТ володіє заданою властивістю, 2) будь-яка точка, яка не належить цій фігурі, заданою властивістю не володіє. Замість другого твердження можна доводити еквівалентне йому твердження, зворотне першому: якщо точка має задану властивість, то вона належить шуканій фігури.
Суть методу геометричних місць полягає в наступному. Дана задача на побудову зводиться до побудови деякої точки, яка в подальшому давала б можливість побудувати всю потрібну фігуру. У процесі аналізу з'ясовується, що ця «ключова» точка володіє декількома (частіше двома) властивостями по відношенню до заданих елементів шуканої фігури. Одне з цих властивостей тимчасово залишається осторонь і знаходиться ГМТ, які відповідають іншим властивостями [2, c. 65].
Потім залучається відкинута властивість і усувається інша властивість з тих, якою повинна володіти шукана «ключова» точка. Знаходиться ГМТ, які відповідають новій сукупності властивостей. Шукана точка повинна належати перетину двох отриманих ГМТ.
1 2 3 4 5 6