Ім'я файлу: ПОТОКИ книга.docx
Розширення: docx
Розмір: 927кб.
Дата: 29.05.2021
скачати

скінченною множиною станів

s₁,

s₂ , ,

s_n,

які залежать від дискрет-

ного параметра. У них зміни можуть відбуватися лише у фіксовані

моменти часу

t 0, 1, ...,

причому стан системи в наступний момент

залежить лише від того, у якому стані система перебуває в даний мо- мент часу і не залежить ні від динаміки переходів зі стану в стан у по- передні моменти часу, ні від того, як система потрапила в теперішній стан. У цьому розділі ми будемо вивчати стохастичні процеси, які є залежними від неперервного параметра. У системах, у яких відбува- ються такі процеси, переходи з одного стану в інший можливі в будь- які моменти часу. Вказані стохастичні процеси застосовуються в різ- них розділах природознавства, техніки та економіко-математичного моделювання.

Нехай досліджується деяка система S, яка в кожний фіксований

момент часу

t t_i

може перебувати в одному з несумісних станів

s₁ , s₂ , ,

s_n.

У загальному випадку число станів системи може бути

як скінченним, так і зліченним. При вивченні випадкових процесів, які відбуваються в системах з дискретними станами, важливу роль відіг- рають ймовірностістанів.

Означення.Ймовірність події, яка полягає в тому, що в момент t

система ^Sбуде знаходитися в стані

s_i ,

називається ймовірністю

i-го станувмомент часуt:

p_it_  P_S_t_  s_i,
i 1, 2,  n.
(2.1)

Оскільки для будь-якого tвипадкові події

^S^t ^{ si,}

i 1, 2,  n

попарно несумісні та утворюють повну групу подій, то сума ймовір- ностей цих подій для кожного tдорівнює одиниці:

_ ^pi^t ^{ 1.}

i  1
(2.2)

цесомбезпіслядії), якщо для будь-якого моменту часу t₀

ймовір-

ність будь-якого стану системи в майбутньому (при

t t₀ )

зале-

жить лише від його стану в теперішньому (при

t t₀ )

і не залежить

від того, як і скільки часу цей процес розвивався в минулому (при

t t₀ ).

Іншими словами, для марковського випадкового процесу при фік- сованому теперішньому майбутнє не залежить від минулого.

На практиці марковські процеси у чистому вигляді зустрічаються не досить часто, але достатньо часто зустрічаються процеси, які з пев- ним наближенням можна вважати марковськими. Марковськіпроцесиє одним із важливих розділів економіко-математичного моделювання; вони визначають окремий вид ймовірнісних моделей різноманітних процесів, що відбуваються у фінансово-економічних системах.

Будемо вважати, що переходи системи Sзі стану s_i

у стан s_j

від-

буваються під впливом деякого потоку подій. Теорію марковських про- цесів з дискретними станами і неперервним часом вивчають у припу- щенні, що переходи зі стану в стан у системі відбуваються під впли- вом пуассонівських потоків подій (не обов’язково стаціонарних). Саме властивість відсутності післядії в потоці Пуассона дозволяє при фік-

сованому теперішньому стані (стан s_i

системи в момент часу t) не

враховувати, як і коли система набула цього стану.

Зауважимо, що як тільки настає перша подія потоку після деякого

моменту часу

t₀ ,

то система Sвідразу переходить зі стану s_i

у стан

s_j.

Таким чином, перехід системи Sзі стану s_i

у стан s_j

відбува-

ється під впливом лише першої події потоку

П_ij,

хоча теоретично цей

перехід пояснюється впливом “усього” потоку подій

П_ij,

що дозволяє

^{використовувати поняття інтенсивності }^t

потоку

^Пij.

Слід зазначити, що, на відміну від ланцюгів Маркова (випадково-

го процесу Маркова з дискретними станами і дискретним часом), за-

^{мість ймовірностей переходу pij}^k ^{[11, с. 55], для процесу Маркова}

із неперервним часом використовують інші характеристики – щільно-

стіймовірностейпереходу

^ij

зі стану s_i

у стан

s_j.

Розглянемо детальніше це поняття. Нехай

^pij<sup>t;

t</sup>^,

i j,

t 0 

ймовірність того, що система S, яка знаходиться в стані

s_i ,

за промі-

^{жок часу} ^{t; t  t} ^{перейде зі стану si}

у стан

s_j.

Зауважимо, що

^pij<sup>t;

t</sup> ^{ 0,}

i j,

якщо:

• 
  система Sу момент часу tне знаходилась у стані s_i;
  

• 
  система Sу момент часу tзнаходилась у стані
  

s_i ,

але за час t

вона перейшла у стан

s_k, відмінний від стану

s_j:

j k;

• 
  система Sу момент часу tзнаходилась у стані s_i і протягом про-
  

^{міжку часу tзалишалась у цьому стані: pii}^{t; t} ^{ 0,}

i 1, 2,  n.

Означення.Щільністю ймовірності переходу системи Sзі стану

s_i у стан s_j

у момент часу tназивається величина

^ij
З рівності (2.3) маємо

^t ^{ lim}

t0

^pij^{t; t}

t ^.
(2.3)

^{pij(t; t)  ij}^t ^{ t,}

t 0.

(2.4)

Отже, в загальному випадку _ij(t) є функцією від t;

_ij(t) набуває

^{невід’ємних значень, на відміну від pij}<sup>t;

t</sup>^,

може приймати значен-

ня, які більші за 1;

_ii(t)  0,

i 1, 2, , n.

Теорема2.1.Щільність ймовірності переходу

_ij(t)

системи Sзі

стану s_i

у стан s_j

у момент часу tпід впливом пуассонівського по-

току

^Пij

^{дорівнює інтенсивності }^t

потоку

П_ij.

Доведення

Згідно з формулою (2.4) ймовірність того, що система Sза промі-

жок часу t

перейде зі стану s_i

у стан

s_j,

дорівнює

^{pij(t; t)  }_ij^t ^{ t,}

t 0.

Ця ймовірність – це ймовірність того, що за час t

відбулася хо-

ча б одна подія пуассонівського потоку, під впливом якої відбувається

перехід системи Sзі стану s_i

у стан

s_j.

Для стаціонарного потоку Пуассона ймовірність появи хоча б однієї

події за час t, згідно з (1.3), дорівнює

^Pt

^{k 1} ^{ 1  Pt}

(0)  1  e^t.

Використовуючи розвинення функції

_et

в ряд Маклорена

^t2 ^t3

e^t 1  t   , 2! 3!

отримаємо наближену рівність:

e^t 1   t,

тоді
^Pt^{k 1} ^{ 1 Pt(0)  11 t  t,}
t 0.

Оскільки

^{pij(t; t)  Pt}^{k 1}^{, маємо}

_ij(t)  t (t)  t.

Отже,

^_ij^t ^{ }^t^,
(2.5)

що й потрібно було довести.
Зауважимо ще раз, що для того, щоб випадковий процес із непере- рвним часом, який відбувається в системі з дискретними станами, був марковським, необхідно і достатньо, щоб всі потоки подій, що перево- дять систему зі стану в стан, були пуассонівськими (стаціонарними чинестаціонарними).

У зв’язку з цим системи, у яких відбуваються марковські випадко- ві процеси з дискретними станами та неперервним часом, називають пуассонівськимисистемами.

Означення.Процес Маркова з дискретними станами і неперервним

часом називається однорідним, якщо для будь-яких iта j, i j,

i 1, 2, , n,

j 1, 2, , n

щільність ймовірності переходу

^ij^t

системи зі стану s_i

до стану s_j

не залежить від часу t,

тоб-

^{то }_ij^t ^{ }_ij<sup> const.

Якщо ж хоча б для однієї пари</sup> ^{i; j}^{, i jщільність ймовірності}

переходу _ijt_ залежить від t, то процес називається неоднорідним.

Надалі будемо розглядати однорідні марковські процеси з дискрет- ними станами та неперервним часом.

Для наочності при дослідженні марковських випадкових процесів з дискретними станами і неперервним часом, як і у випадку ланцюгів

цес з неперервним часом. Відсутність стрілки між станами s₂

і s₁

вка-

зує на те, що щільність ймовірності відповідного переходу дорівнює

нулю: ₂₁  0. Аналогічно маємо ₃₁  0, ₁₄  0, ₄₃  0.

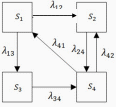
Рисунок 2.1

Щільності ймовірностей переходів
_ij,

як і перехідні ймовірно-

сті

^pij

у випадку ланцюга Маркова, можна записати у вигляді квадрат-

ної матриці
^{ }11
^12
^13

...
^1n^




^ 21

^22

^23

...



^2n^



  ^





...

...

...

...

...

...

...

...

...

...

...

...

... ^



... _

... ^



 ^n1

^n2

^n3
...



^nn

де ₁₁  ₂₂    _nn 0.

2. Диференціальні рівняння Колмогорова

Нехай досліджується деяка система S, яка в кожний фіксова-

ний момент часу

t t_i

може перебувати в одному з несумісних станів

s₁ , s₂ , ,

s_n.

Для опису випадкового процесу, який відбувається в си-

стемі, використовують ймовірності станів системи (2.1):

^p1 ^t<sup>,

p2</sup> ^t<sup>, ,

pn</sup>^t^.

Якщо для кожної пари станів s_i

і s_j

відомі інтенсивності пуассо-

нівського потоку подій

_ij ,

то можна скласти диференціальні рівняння

для ймовірностей станів.

Теорема 2.1. Ймовірності станів
^pi^t^,
де i 1, 2, , n
системи

S, у якій відбувається однорідний марковський процес з неперервним

часом, є розв’язком системи диференціальних рівнянь:


^dpi^t


dt

^{  } _ ^{  p}^t ^

_ ^ _ji^p_j^t^.

n

n
(2.6)

^ij i
Доведення

_ j 1, j i _

j 1, j i

Розглянемо систему ^S, яка в кожен момент часу tможе перебу-

вати в одному із несумісних станів s₁ , s₂ , ,

s_n. Надамо моменту часу

tприріст tі знайдемо ймовірність

p_it t того, що в момент часу

t t

система буде знаходитись у стані

s_i.

Ця подія може відбутися внаслідок однієї з подій

^Ai^{t, t}
або

^Bi^{t, t}

^{де Ai}^{t, t}

– подія, яка полягає в тому, що система Sу момент

часу tзнаходилась у стані s_i

і за час ^t

не вийш-

ла з цього стану, тобто не перейшла в інший стан

s_j,

j 1, 2, , n,

j i;

^Bi^{t, t}

– подія, яка полягає в тому, що система Sу момент

часу tзнаходилась у деякому стані

s_j ,

j 1, 2, ,

, n,

j i,

і за час ^t

перейшла у стан

s_i.

Оскільки події

^Ai^{t, t} <sup>та

Bi</sup>^{t, t}^{– несумісні, то за теоремою про}

суму несумісних подій маємо

p_it t_  P_ A_it, t_  P_B_it, t_.

(2.7)

Подія

^Ai^{t, t}

може бути подана у вигляді добутку двох подій:

^Ai^{t, t} ^{ Si}^t ^{ Ci}^{t, t}

^{де Si} ^t

• 
  подія, яка полягає в тому, що система Sу момент ча-
  

су tзнаходилась у стані s_i;

^Ci^{t, t}

• 
  подія, яка полягає в тому, що система Sпротягом ча-
  

су ^t

залишалась у стані

s_i.

Тоді за теоремою про ймовірність добутку залежних подій маємо

P_ A_{i }t, t_  P_S_{i }t_  C_{i }t, t_  P_S_{i }t_ P_C_{i }t, t_ / S_{i }t_ 

 p_{i }t_  P_C_{i }t,

t_ / S_it_.

(2.8)

Знайдемо ймовірність події

P_C_it, t_ / S_it_.
Розглянемо проти-

лежну подію

^Ci^{t, t}^,

яка полягає в тому, що система Sза час ^t

перейде зі стану s_i

що

до іншого стану

s_j ,
n

j 1, 2, , n,

j  i. Зрозуміло,

^Ci^{t, t} ^



j  1, j i

^Dij^{t, t}

^{де Dij}^{t, t}^,

j i

• 
  подія, яка полягає в тому, що система Sза
  

час ну

t

s_j.

перейде зі стану s_i

до іншого ста-

Оскільки події

^Dij^{t, t}

несумісні, маємо:

n n

P_C_it, t_ / S_it_  _ P_D_ijt, t_ / S_it_  _ p_ijt, t_.

j 1, j  i j 1, j  i

Враховуючи (2.4), маємо

Тоді

P_C_it, t_ / S_it_ 