
Ім'я файлу: курсова 3 курс 1 семестр.docx
Розширення: docx
Розмір: 218кб.
Дата: 06.05.2021
скачати
Пов'язані файли:
ср3.doc
17план конспект уроку Покупки у Лондоні.docx
Розширення: docx
Розмір: 218кб.
Дата: 06.05.2021
скачати
Пов'язані файли:
ср3.doc
17план конспект уроку Покупки у Лондоні.docx
2.3.2 Симетрія
Осьовою симетрією називається таке перетворення, при якому кожній точці М даної фігури F ставиться у відповідність точка
 , яка симетрична їй відносно прямої l – осі симетрії. Зазвичай осьову симетрію фігури Fвідносно прямої позначають
, яка симетрична їй відносно прямої l – осі симетрії. Зазвичай осьову симетрію фігури Fвідносно прямої позначають 
 | Використовуючи метод осьової симетрії, поряд із даними та шуканими фігурами розглядають фігури, симетричні деяким із них відносно обраної осі. Вдало вибравши вісь симетрії, можна значно полегшити процес відшукання розв’язку задачі. |
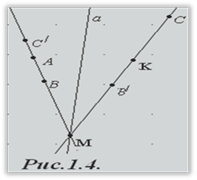
Задача8. Дано пряму а та дві точки Ві С по різні боки від неї. Знайти на цій прямій таку точку М, щоб кут
 мав пряму а своєю бісектрисою.)
мав пряму а своєю бісектрисою.)  | Аналіз. Нехай М – шукана точка, вона знаходиться на прямій а, і є вершиною деякого трикутника АМК. При цьому задані в умові точки В і С належать відповідно прямим АМ і КМ симетричними відносно прямої а. |
Тому при симетричному відображенні точок В і С відносно прямої а одержимо точки
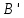 та
та  , що належатимуть відповідно прямим
, що належатимуть відповідно прямим 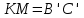 та
та  . Таким чином точка М може бути побудована, як точка перетину прямих
. Таким чином точка М може бути побудована, як точка перетину прямих  та
та 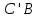 .
. Побудова. 1)
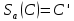 ; 2)
; 2) 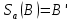 ; 3)
; 3)  .
.Доведення. Випливає з аналізу й побудови, очевидне.
Дослідження. В умові задачі не сказано, як саме розміщені точки В та С. Можливі два випадки: 1) точки В та С належать прямій перпендикулярній до прямої а, тоді шукана точка М буде точкою перетину прямих ВС та а; 2) прямі ВС та а не є перпендикулярними, тоді для відшукання точки М слід скористатися поданим вище алгоритмом.
2.3.3 Поворот
Поворотом фігури F навколо деякої точки О на кут 𝛼,
 називається перетворення при якому точка О залишається нерухомою, будь-якій іншій точці М ставиться у відповідність така точка
називається перетворення при якому точка О залишається нерухомою, будь-якій іншій точці М ставиться у відповідність така точка  , що
, що  i
i  .
.При використанні методу обертання, деяку шукану чи дану фігуру намагаються повернути навколо доцільно обраного центру на відповідний кут так, щоб полегшити проведення аналізу чи безпосередньо прийти до розв’язку даної задачі. Для здійснення повороту потрібно вибрати центр, кут та напрям повороту, при чому за центр повороту обирають точку, положення якої є визначеним на площині. Окремо виділяють поворот на 180˚ - перетворення, яке називають центральною симетрією. Для того щоб задати центральну симетрію необхідно вказати центр симетрії або пару відповідних точок.
Задача 9. Дані прямі aта l і точка С, що їм не належить. Побудувати правильний трикутник ∆АВС, вершини А,В якого належать відповідно прямим а, b,
 ,
, 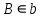 . (1)
. (1)| | Нехай ∆АВС – шуканий. Значить  (=60˚). Якщо задати напрям повороту за годинниковою стрілкою, то один з орієнтовних кутів АСВ або ВСА буде мати величину 60˚. (=60˚). Якщо задати напрям повороту за годинниковою стрілкою, то один з орієнтовних кутів АСВ або ВСА буде мати величину 60˚. |
Якщо АСВ=60˚, то при повороті на 60˚ навколо точки С точка А перейде в точку В

Якщо
 , то при цьому ж повороті точка
, то при цьому ж повороті точка 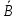 перейде в
перейде в  , тобто
, тобто  .
.Але оскільки при повороті зберігається належність точки і прямої, то якщо при цьому повороті прямі а, bпереходять відповідно в
 , то
, то 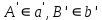 , тобто
, тобто  ,
,  .
. Тим самим вершини В та А шуканих трикутників АВС та
 можна отримати з формул
можна отримати з формул  ,
,  .
. Обернений поворот (проти годинникової стрілки) дасть точки А та
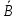 (можна отримати як перетин прямої а з колом
(можна отримати як перетин прямої а з колом  ).
).Дослідження формул
 ,
,  дає, що:
дає, що:Якщо
 ,
, 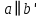 , то отримані точки В та
, то отримані точки В та  дають два рішення (точки А, В, С не можуть лежати на одній прямій, так як точка А отримується з точки В поворотом на 60˚, а не 180˚ або 360˚).
дають два рішення (точки А, В, С не можуть лежати на одній прямій, так як точка А отримується з точки В поворотом на 60˚, а не 180˚ або 360˚).Якщо
 , тобто кут між aта b, в якому лежить точка С, рівний 120˚, але при цьому
, тобто кут між aта b, в якому лежить точка С, рівний 120˚, але при цьому  ,
,| | тобто точка С не лежить на бісектрисі кута між aта b, то точка В – ні. Але при цьому автоматично  , ,  , тобто точка , тобто точка  існує – один розв’язок. існує – один розв’язок. |
Якщо
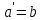 , тобто кут між aта bдорівнює 120˚ і точка С лежить на бісектрисі кута 120˚, існує нескінченна кількість
, тобто кут між aта bдорівнює 120˚ і точка С лежить на бісектрисі кута 120˚, існує нескінченна кількість | | розв’язків, оскільки при повороті навколо точки С на 60˚ пряма а переходить в пряму  , будь-яка точка А прямої а перейде в точку В на прямій , будь-яка точка А прямої а перейде в точку В на прямій  , котрі утворять шуканий трикутник. , котрі утворять шуканий трикутник. |
2.3.4 Інверсія
Інверсією відносно кола К(О, r) називається перетворення площини при якому точка О не має образу, а будь-якій іншій точці А площини ставиться у відповідність така точка
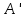 для якої виконуються дві умови: 1)
для якої виконуються дві умови: 1)  ; 2)
; 2) 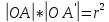 . Коло К(О, r) називається колом фігури F позначають
. Коло К(О, r) називається колом фігури F позначають  .
.Задача 10. Дане перетворення відображає кожну точку кола інверсії саму в себе, внутрішні точки круга інверсії в зовнішні, а зовнішні у внутрішні. Для того щоб побудувати образ довільної точки А при заданій інверсії
 необхідно врахувати положення даної точки відносно кола інверсії.
необхідно врахувати положення даної точки відносно кола інверсії. 
Нехай точка А – внутрішня відносно даного кола інверсії K(O,r). Тоді для побудови
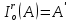 необхідно виконати наступні дії: 1) ОА; 2)
необхідно виконати наступні дії: 1) ОА; 2)  ; 3)
; 3)  ; 4)
; 4)  – дотична до кола інверсії в точці Р; 5)
– дотична до кола інверсії в точці Р; 5) 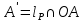 – шукана точка. Для побудови зовнішньої точки, виходячи з властивості взаємності, потрібно виконати в оберненому порядку побудови зроблені в першому випадку.
– шукана точка. Для побудови зовнішньої точки, виходячи з властивості взаємності, потрібно виконати в оберненому порядку побудови зроблені в першому випадку. При розв’язуванні задач на побудову досить часто доводиться будувати інверсію прямої та кола.
Особливості побудови образів прямих та кіл при інверсії:
Пряма, що не проходить через центр інверсії, переходить в коло, яке проходить через центр інверсії;
Пряма, що не проходить через центр інверсії, переходить в коло, що проходить через центр інверсії.
Коло, що проходить через центр інверсії, переходить в пряму, що проходить через центр інверсії;
Коло, що не проходить через центр інверсії, переходить в коло, що також не проходить через центр інверсії.
Для того, щоб вирішити задачу на побудову методом інверсії роблять припущення, що задача розв’язана. Зображують задані фігури і шукані. Потім дані фігури, шукану або їх елементи піддають перетворенню інверсії так, щоб одержати нову, допоміжну задачу, яка розв’язується простіше, ніж дана. Побудувавши допоміжну фігуру і знайшовши її образ при тій самій інверсії, отримують розв’язок задачі. Для використання даного методу слід вдало вибрати центр інверсії (доцільно обрати центр інверсії на одному з заданих чи шуканому колі), а радіус обрати таким чином, щоб деякі точки перейшли самі в себе. Слід зазначити, що даний метод з одного боку дає можливість розв’язувати складні задачі, проте з іншого – він є найбільш громіздким, що пов’язано з необхідністю виконання великої кількості побудов.
Задача 11. Дані коло К і дві точки А та В, що не лежать на ньому. Побудувати коло, що проходить через точки А і В та дотикається кола К. Розв’язання:
 | Аналіз. Припустимо, що задача вже розв’язана і γ – шукане коло. Позначимо фігуру, що складається з точок А і В, а також кіл К та γ буквою F. Потім проведемо коло Т з центром в точці А і розглянемо інверсію І, для якої коло Т – коло інверсії. |
Образом фігури F при цій інверсії буде деяка фігура
 , що складається з точки
, що складається з точки 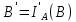 , кола
, кола 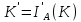 та прямої
та прямої 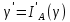 . (точка А, як центр інверсії не матиме образу) враховуючи те, що кола К та γ дотикаються, то їх образи також дотикаються. Фігуру
. (точка А, як центр інверсії не матиме образу) враховуючи те, що кола К та γ дотикаються, то їх образи також дотикаються. Фігуру  легко побудувати, враховуючи те, що
легко побудувати, враховуючи те, що 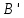 і
і 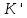 є образами даних фігур, а
є образами даних фігур, а  дотикається до кола
дотикається до кола  . Потім, використавши ту саму інверсію, можна побудувати коло γ, як образ прямої
. Потім, використавши ту саму інверсію, можна побудувати коло γ, як образ прямої  .
.Побудова. Оберемо коло інверсії так, щоб воно перетинало коло К в двох точках. Це полегшить побудову образу кола К.
 ;
;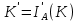 . Для цього достатньо побудувати
. Для цього достатньо побудувати  і провести коло
і провести коло  через точки 1, 2,
через точки 1, 2,  .
. Через точку
 провести дотичну
провести дотичну  до кола К так, щоб вона не проходила через точку А.
до кола К так, щоб вона не проходила через точку А.Будуємо шукане коло
 . Коло γ проходить через точки А, 4 і 5.
. Коло γ проходить через точки А, 4 і 5.Доведення. Так як пряма
 проходить через точку А, то її образ є коло, що проходить через точку А, пряма
проходить через точку А, то її образ є коло, що проходить через точку А, пряма  проходить через точку
проходить через точку  і дотикається кола
і дотикається кола  , тому
, тому  і γ та К дотикаються один до одного.
і γ та К дотикаються один до одного. Дослідження. Дана задача може не мати розв’язків (у тому випадку, коли одна з точок А або В є внутрішньою точкою відносно кола К, а інша - зовнішньою), може мати тільки один розв’язок (якщо, наприклад, точки А і В лежать на дотичній до кола К) і два розв’язки. Для побудови другого розв’язку на рисунку необхідно через точку
 провести другу дотичну
провести другу дотичну  до кола
до кола  і побудувати її образ.
і побудувати її образ.Примітка. Дану задачу можна сформулювати в більш загальну: дано три основні фігури (точка, пряма та коло). Побудувати коло, що дотикається цих фігур (у випадку дотику кола до точки маємо на увазі, що коло проходить через неї). У випадку, коли всі три дані фігури кола, задача називається задачею Апполонія: побудувати коло, що дотикається до трьох заданих кіл. Решта випадків називаються граничними випадками цієї задачі. Метод інверсії зручно використовувати у тому випадку, коли хоча б одна із заданих фігур є точкою.
2.3.5 Метод подібності (Гомотетія)
Гомотетією з центром в точці О та коефіцієнтом
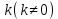 називається перетворення площини при якому довільній точці М ставиться у відповідність така точка
називається перетворення площини при якому довільній точці М ставиться у відповідність така точка 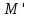 , для якої виконується умова:
, для якої виконується умова:  .
. Метод подібності полягає в тому, що в задачі на побудову опускають одну з умов так, щоб отримати множину подібних геометричних фігур, які задовольняють іншим умовам. Серед отриманої множини фігур буде і шукана фігура, для відшукання якої слід врахувати опущену умову. Даний метод зазвичай використовують у тих випадках, коли серед даних лише один відрізок і кути або співвідношення між відрізками.
Задати гомотетію можна різними способами, наприклад, центром і парою відповідних точок (всі три точки розташовані на одній прямій), двома парами відповідних точок, коефіцієнтом та центром гомотетії. Гомотетію фігури F з центром у точці О і коефіцієнтом k позначають
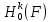 .
. Задача 12. В даний гострокутний трикутник АВС вписати квадрат так, щоб дві його вершини лежали по одній із сторін квадрата.
| | Аналіз. Нехай квадрат DKPE – шуканий, тобто задовольняє умовам: 1) дві вершини лежать на стороні АС; 2) третя вершина лежить на стороні АВ; 3) четверта вершина лежить на стороні ВС. Задачу легко розв’язати, використовуючи метод подібності, для цього опустимо умову 2. |
В результаті ми зможемо побудувати безліч квадратів, подібних шуканому. Розглянемо один з таких квадратів
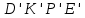 , для побудови шуканого квадрата скористаємося гомотетією відносно вершини
, для побудови шуканого квадрата скористаємося гомотетією відносно вершини  . Вершина К шуканого квадрата, яка лежить на стороні АВ, лежить на прямій
. Вершина К шуканого квадрата, яка лежить на стороні АВ, лежить на прямій 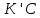 , тобто
, тобто  . Знайшовши точку К легко побудувати решту вершин квадрата.
. Знайшовши точку К легко побудувати решту вершин квадрата. Побудова. 1)
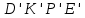 - довільний квадрат (
- довільний квадрат ( ); 2)
); 2) 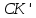 ; 3)
; 3) 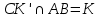 ; 4)
; 4) 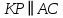 ; 5)
; 5)  ; 6)
; 6) 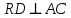 ; 7)
; 7)  – шуканий чотирикутник.
– шуканий чотирикутник.Доведення. Випливає з подібності квадратів.
Дослідження. Дана задача має єдиний розв’язок, оскільки кожний крок побудови виконується однозначно.
2.4 Алгебраїчний метод
Суть алгебраїчного методу полягає в тому, що розв’язок задачі на побудову зводять до побудови деякого відрізка (або декількох відрізків). Вершину шуканого відрізка виражають через величини відомих відрізків за допомогою формули. Потім будують шуканий відрізок за отриманою формулою. Щоб розв’язувати задачі на побудову даним методом, необхідно вміти будувати відрізки задані найпростішими формулами.
Задача 13. (задача про подвоєння квадрата.) Побудувати квадрат, площа якого вдвічі більше площі даного квадрата.
Аналіз. Позначимо сторону даного квадрата через а, а сторону шуканого квадрата через х. Тоді
 ,
,  .
. Побудова. Будуємо тепер відрізок xпо отриманій формулі: x– гіпотенуза рівнобедреного трикутника з катетом a. Побудувавши відрізок x, легко потім побудувати шуканий квадрат.

Висновки
Конструктивна геометрія – найдавніший розділ практичної геометрії, яка і сьогодні має актуальний характер. В практичній діяльності працівникам різних галузей (інженерам, конструкторам, геодезистам, архітекторам, кравцям, столярам та ін.) доводиться виконувати різні геометричні побудови.
Геометричні побудови – традиційно одна з провідних змістових ліній шкільного курсу геометрії. Основна мета вивчення геометричних побудов у школі – навчити учнів виконувати основні побудови циркулем та лінійкою та розв’язувати нескладні комбіновані задачі, які зводяться до виконання основних побудов.
Створивши динамічні моделі, аналізуючи динамічні вирази, можна проводити дослідження ГМТ, встановлювати значення певних величин, шукати закономірності.
Список використаної літератури
1. Васильева М.В. Конструктивная геометрия (геометрические построения на евклидовой плоскости) – вид. МГПИ им. В.И. Ленина 1988
2. Трохименко В.С. Конструктивна геометрія Вінниця - 2012
3. Адлер А. Теория геометрических построений / Переклад з німецького Г. М. Фихтенгольца. – Вид. 3-тє. – Л.: Учпедгиз, 1940. – 232 с.
4. Слєпкань З.І. Методика навчання математики: Підручник для студентів математичних спеціальностей педагогічних навчальних закладів. – К.: Зодіак-ЕКО, 2000. – 512 с.
5. Мазаник А.А. Задачи на построение по геометри в восьмилетней школе – вид. «Народная аскета» Минск 1967
6. Бурда М.І. Розв’язування задач на побудову в 6-8 класах - 1986
1 2 3