
48.Порівняння двох середніх нормальних генеральних сукупностей
Порівняння двох середніх нормальних генеральних сукупностей, дисперсії яких відомі (незалежні вибірки)
Нехай генеральні сукупності
Потрібно з вибіркових середніх при заданому рівні значущості
Конкуруючою гіпотезою є
З огляду на те, що вибіркові середні є незміщеними оцінками генеральних середніх, тобто
У якості критерію перевірки нульової гіпотези візьмемо випадкову величину
 , (4)
, (4)яка є нормованою нормальною розподіленою випадковою величиною [2].
Двосторонню критичну область будуємо, виходячи з вимоги, щоб імовірність влучення критерію в цю область у припущенні справедливості нульової гіпотези дорівнювала б прийнятому рівню значущості
Можна показати, що найбільша потужність критерію досягається при рівності ймовірностей улучення критерію в кожний із двох інтервалів критичної області, тобто при
Із симетрії нормованої нормальної величини випливає симетрія і критичних точок, тобто
чи
Далі треба обчислити значення критерію, що спостерігається
 .
.Якщо виявиться, що
49.Перевірка гіпотези про нормальний розподіл генеральних сукупностей
Перевірка гіпотези про закон розподілу здійснюється за допомогою спеціально підібраної величини – критерію узгодженості.
Існує декілька критеріїв узгодженості: , Колмогорова, Смірнова К. Пірсона, тощо.Для перевірки гіпотези про нормальний закон розподілу генеральної сукупності скористаємось критерієм Пірсона, перевагою якого є те, що він застосовується не тільки до нормального, але і до інших розподілів.
Для того, щоб при заданому рівні значущості перевірити нульову гіпотезуН0: генеральна сукупність розподілена нормально, потрібно спочатку обчислити теоретичні частоти , а потім значення критерію за даними вибірки:
і за таблицею критичних точок (додаток 4), за заданим рівнем значущості і числом ступенів вільностіk=s-3 знайти критичну точку
Якщо
Якщо
Обсяг вибірки повинен бути достатньо великим, принаймні не менше 50.
Отже, необхідно перевірити гіпотези про нормальний розподіл генеральних сукупностей X та Y, використовуючи критерій погодженості Пірсона.
При рівні значущості перевіримо гіпотезу про нормальний розподіл генеральної сукупності, якщо відомі емпіричні ( ) і теоретичні частоти
50.Методика обчислення теоретичних частот нормального розподілу
Розглянемо один із способів обчислення теоретичних частот в припущенні, що генеральна сукупність розподілена нормально.
1. Весь інтервал спостережувальних значень Х вибірки обсягу ділять на частинних інтервалів
 . Знаходять середини частинних інтервалів
. Знаходять середини частинних інтервалів  . Одержуємо варіаційний ряд
. Одержуємо варіаційний ряд| | | | ... | |
| | | | ... | |
2. Обчислюємо вибіркову середню
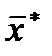 і вибіркове середнє квадратичне відхилення
і вибіркове середнє квадратичне відхилення  .3. Нормуємо випадкову величину Х, тобто переходимо до величини
.3. Нормуємо випадкову величину Х, тобто переходимо до величини  і обчислюємо кінці інтервалів
і обчислюємо кінці інтервалів 
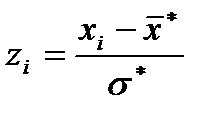 і
і  . (15.7)
. (15.7)При цьому найменше значення , тобто , беруть рівним
4. Обчислюємо теоретичні ймовірності
 за формулою
за формулою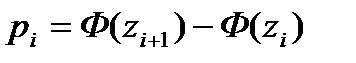 , (15.8)
, (15.8)де
 - функція Лапласа.
- функція Лапласа.5. Обчислюємо шукані теоретичні частоти за формулою
 . (15.9)
. (15.9)51.Статистична та кореляційна залежності
Однією із задач математичної статистики є встановлення й оцінювання залежності однієї випадкової величини від іншої або від кількох інших величин.
Розглянемо випадкові величини Х та Y. В загальному випадку вони можуть бути залежними або незалежними.
Випадкові величини будуть незалежними, якщо розподіл однієї з них не залежить від того, якого значення набуде інша. Коли ця умова не виконується – випадкові величини залежні. При цьому вони можуть бути пов’язані функціональною або статистичною залежністю.
Якщо кожному можливому значенню випадкової величини Х відповідає єдине випадкове значення випадкової величини Y, то існує функціональна залежність між величинами Y та Х. Це найсильніша залежність. Тоді Y являє собою функцію випадкового аргументу Х, тобто Y = j(x).
Статистичною називають таку залежність, при якій зміна однієї величини приводить до зміни розподілу іншої. Зокрема, статистична залежність виявляється у тому, що при зміні однієї величини змінюється середнє значення іншої; така залежність називається кореляційною.
52.Знаходження довірчого інтервалу для математичного сподівання нормально розподіленої ознаки Х якщо середнє квадратичне відхилення
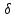 відоме
відоме


53. Знаходження довірчого інтервалу для математичного сподівання нормально розподіленої ознаки Х якщо середнє квадратичне відхилення
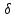 невідоме
невідоме


54.Знаходження довірчого інтервалу для середнього квадратичного відхилення
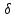 нормально розподіленої ознаки
нормально розподіленої ознакиДовірчий інтервал для оцінки середньоквадратичного відхилення нормального розподілу Нехай кількісна ознака X генеральної сукупності розподілена за нормальним законом. Треба знайти довірчий інтервал, що покриває середньоквадратичне відхилення генеральної сукупності із заданою надійністю Рдов=. Оскільки треба оцінити невідоме середньоквадратичне відхилення генеральної сукупності по виправленому вибірковому середньоквадратичному відхиленню s, потрібно щоб виконувалося співвідношення

де Zi (i =1, 2,…, n) – нормальні, нормовані незалежні величини, тобто їх математичне сподівання дорівнює нулю, середнє квадратичне відхилення дорівнює одиниці і кожна з них розподілена за нормальним законом.



1 2 3 4 5 6 7